|
Das Rätsel der
unterschiedlichen Resonanzkurven beim elektromagnetischen
Schwingkreis (Parallelresonanzkreis)
L-Messung durch die
Resonanzfrequenz?
|
Haben Sie sich nicht auch schon gewundert, dass in manchen Schulbüchern
Resonanzkurven beim elektromagnetischen Schwingkreis mit ganz
unterschiedlichem
Verlauf abgebildet sind, auch wenn es sich immer um einen
Parallelresonanzkreis
handelt?
Haben Sie sich nicht auch schon gefragt, warum Messungen der Induktivität
L mit unterschiedlichen Methoden ganz unterschiedliche Ergebnisse liefern?
Übliche Verfahren der L-Messung in der Schule sind
Wegen seiner Einfachheit wird in der Schule meistens das Verfahren b)
angewandt. Wann ist das eine gute Wahl?
Bei mechanischen Schwingungen wurden ähnliche Fragen anderswo
untersucht [ZIP-Datei mit Handbuch
(und Programm)].
Im Folgenden soll ein elektromagnetischer Schwingkreis mit
vernachlässigbarer (innerer) Dämpfung untersucht werden. Dabei wird der
Schwingkreis durch Ankopplung an einen Funktionsgenerator zu erzwungenen
Schwingungen angeregt. Dabei ist klar, dass wegen der quadratischen
Beziehung L·C = 1/ω02 ein Fehler in
der Resonanzfrequenz einen doppelt so großen Fehler in der L-Messung
zur Folge hat.
Es sollen verschiedene Kopplungsarten durchgespielt werden. In den
Schulbüchern ist meistens induktive Kopplung (Abb. 1) zu finden,
vielleicht
mit der Idee, dass dabei Schwingkreis und Erreger weitgehend getrennt
erscheinen,
so dass der Schwingkreis als eigenständiges Gebilde, sozusagen wie ein
freier elm. Schwingkreis betrachtet werden kann. Dieser Fall soll als
erster
theoretisch untersucht werden. Ist die Idee haltbar?
Die Theorie zu vier Kopplungsarten wird im
Anhang mit zwei unterschiedlichen Methoden
durchgerechnet: Die erste Schaltung wird mit Hilfe eines Systems
gekoppelter
Differentialgleichungen behandelt, die weiteren mit Hilfe von komplexen
Widerständen. Dabei gilt für die Spule ZL = i·ω·L und für den
Kondensator ZC
= - i/ω·C). Durch die imaginäre Einheit i werden Phasenverschiebungen
zwischen Strömen und Spannungen berücksichtigt.
Die Ergebnisse waren für mich einigermaßen
überraschend!
Für mechanische Schwingungen wurde Resonanz bei den verschiedenen
Kopplungsarten bereits anderswo
untersucht.
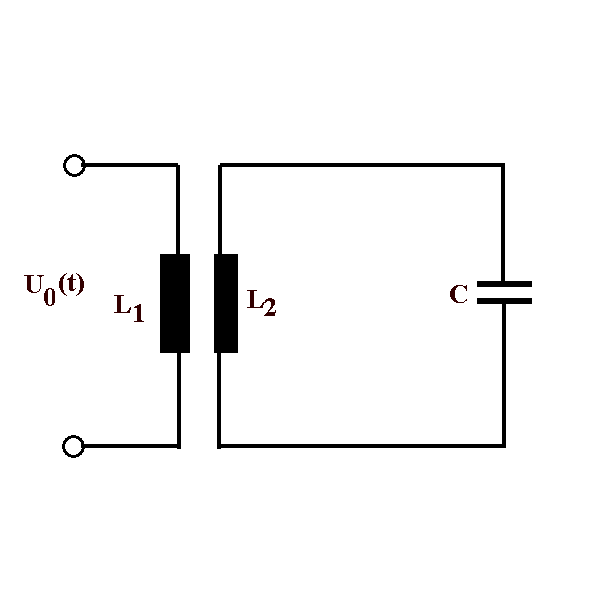 ´ ´
Abb. 1: Induktive Kopplung
|
Abb. 1: Der Generator soll
eine Spannung U0(t) liefert, für die wir den Ansatz
machen: U0(t) = U00 exp (i(ω t-δ)). δ soll
dabei eine mögliche Phasenverschiebung zwischen den Stromstärken
und der Generatorspannung sein. Um die Schreibweise zu
vereinfachen, schlagen wir die Phasenverschiebung δ zur
Generatorspannung hinzu. Eine Rechnung, die Sie im Anhang
A nachlesen können, liefert dabei
das Ergebnis der Abb.1a für die Resonanzkurve:
Für kleine Frequenzen verhält sich die Spannung an der Spule 2
(UL0) wie ω2, für sehr große Frequenzen
strebt der Betrag der Spannung gegen eine Konstante U00
√L2/L1 k/(1 - k2) . k ist
dabei eine Abkürzung, die mit der Gegeninduktivität M = k √ L1·L2
zusammenhängt. k misst sozusagen die Kopplung zwischen beiden
Stromkreisen. L2 ist die Induktivität des
Schwingkreises, L1 die der Kopplungsspule. Die
Frequenz der Spannungssingularität ist gegenüber ω0 =
1/√ L2·C erhöht: ωmax2
= ω02 1/(1 - k2).
Nur bei sehr schwacher Kopplung (k << 1) ist diese
Verschiebung vernachlässigbar.
Der asymptotische Wert der Schwingkreisspannung ist bei k =
0,1 ca. 10 % von U00√L2/L1 ,
wobei U00 die Generatorspannung ist. Bei reiner
Transformation hätte man U00 √L2/L1
erwartet.
|
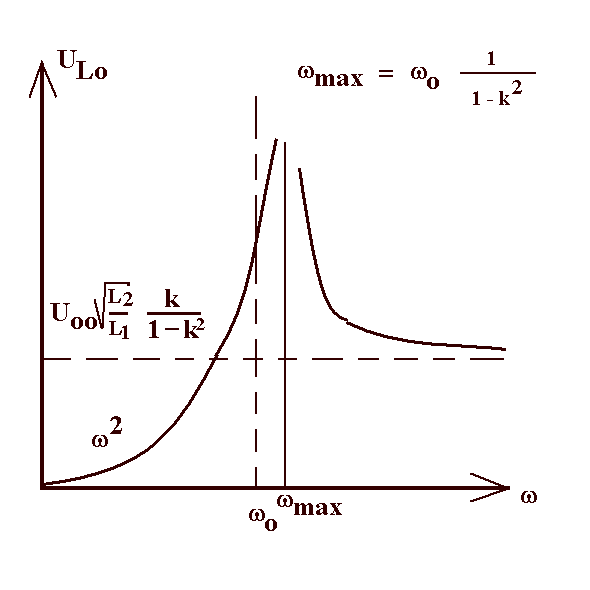
Abb. 1a: Die Resonanzkurve entspricht beim
mechanischen Pendel der Beschleunigungskopplung
(wie beim Seismographen). Da in fast allen Fällen hier eine
Dämpfung außer acht gelassen wird, wird als Stelle des "Maximums
der Schwingkreisspannung" die Frequenz der Polstelle verwendet.
Bei k = 0,1 ergibt sich ωmax = ω0·1,005,
also recht brauchbar. 5% Fehler in der Resonanzfrequenz
entsprechen bei der L-Messung einem Fehler von ca. 10%.
Siehe Theorie: Anhang A
|
| In den folgenden drei Fällen ist die Theorie
deutlich einfacher, weil es naheliegend ist, mit komplexen
Widerständen zu arbeiten (Anhang B). Das
asymptotische Verhalten ist auch ohne die Theorie, also elementar,
zu erschließen (siehe Anhang C). Wenn es
die Sache Wert wäre, könnten das auch Schüler durchführen. |
|
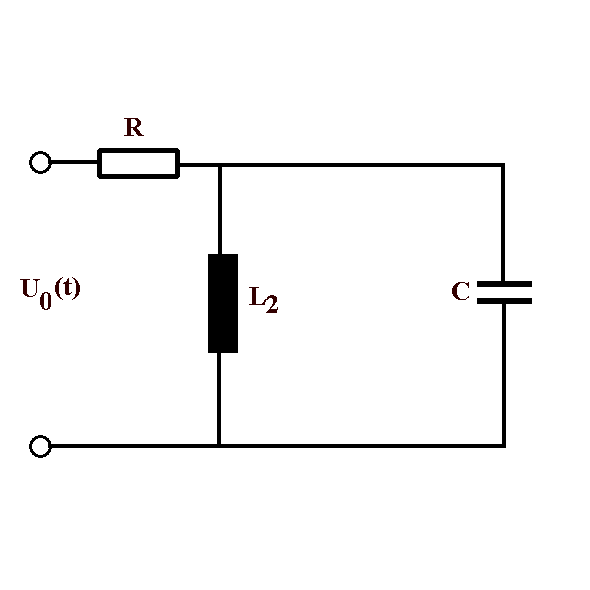 |
| Abb. 2: galvanische Kopplung |
|
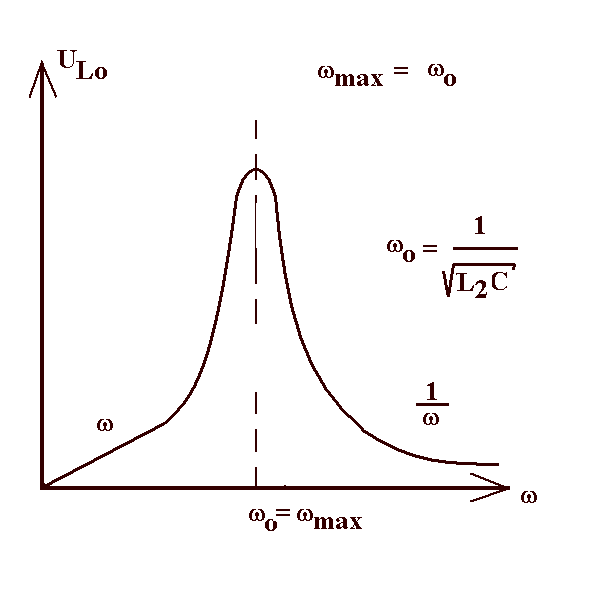
Abb. 2: Für rein galvanische Kopplung ergibt
sich eine Resonanzfrequenz (mit endlicher Spannung) genau bei
der Eigenfrequenz ω0 des Schwingkreises.
Für kleine Frequenzen ω wächst die Schwingkreisspannung linear
an, für sehr große Frequenzen fällt sie mit 1/ω.
Die maximale Spannung kann die Generatorspannung nicht
überschreiten. Das Maximum liegt gerade da, wo sich die beiden
Ströme im Schwingkreis gegenseitig aufheben (oder anders: wo ein
reiner Kreisstrom fließt). Dann ist R stromlos, es kann kein
Spannungsabfall an R entstehen und es kann keine weitere Energie
vom Generator geliefert werden, die die Amplitude ansteigen
ließe.
|
|
|
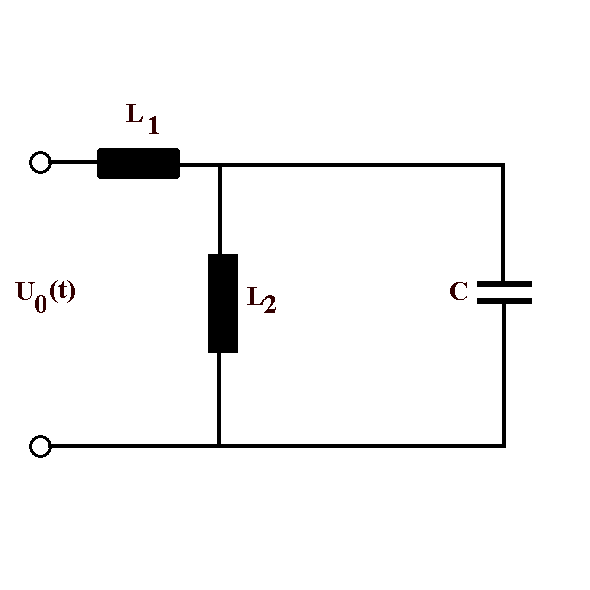 |
| Abb. 3: induktiv-galvanische Kopplung |
|
Abb. 3: Diese Art der induktiven Ankopplung ist
relativ unüblich.
Die Schwingkreisspannung geht für wachsendes ω von einem
endlichen Wert aus (der im Grenzfall schwacher Kopplung U00
ist), und fällt für ω => unendlich wie 1/ω2.
Die maximale Spannung bei ω = ω0
√ (1 + L2/L1) ist je
nach Verhältnis der Induktivitäten zu höheren Frequenzen
verschoben.
Wenn k = L1/L2 = 0,1 ist, beträgt der
asymptotische Wert der Schwingkreisspannung ca. 90 % der
Generatorspannung. Die Frequenz des Spannungsmaximums ist - je
nach dem Verhältnis der Induktivitäten - evtl. ein Vielfaches
größer als die "Idealfrequenz" ωo .
Das ist wohl einer der Gründe, weshalb diese Schaltung zum
Zweck der L-Messung nicht eingesetzt wird.
|
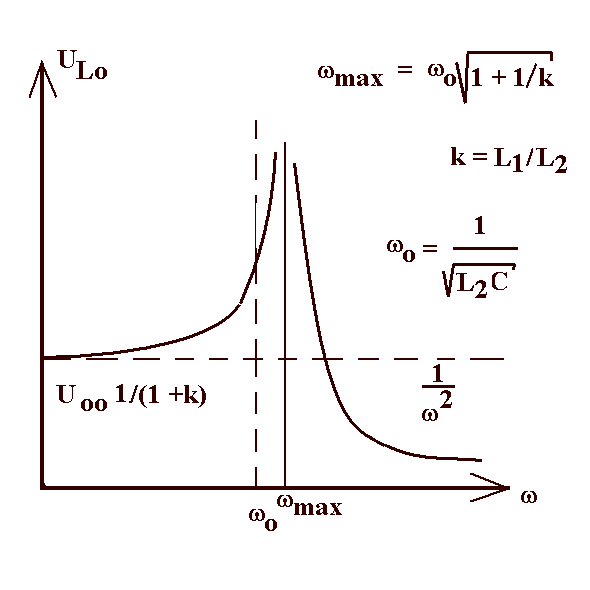 |
| Abb. 3a: Die Resonanzkurve entspricht beim
mechanischen Pendel der Aufhängungskopplung,
also der Situation, wo der Aufhängepunkt des
Federpendels periodisch auf und ab bewegt wird. Wenn
Schulbücher Resonanz in der Mechanik behandeln, wählen
sie in der Regel diesen Fall aus. Siehe Theorie. |
|
|
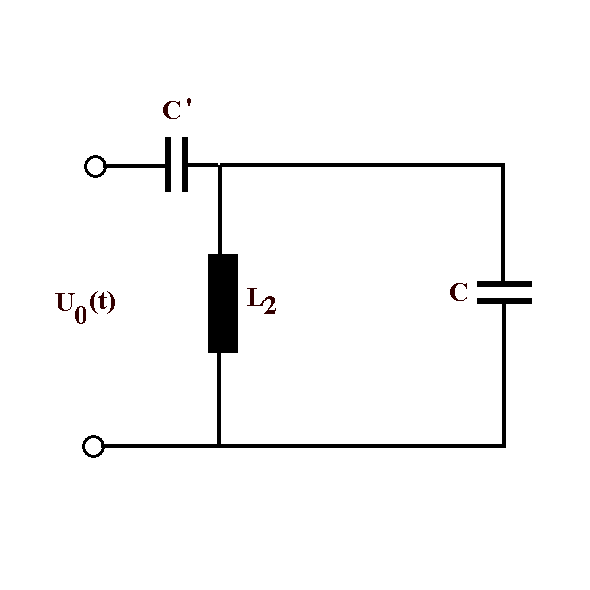 |
| Abb. 4: kapazitive Kopplung |
|
Abb. 4: Bei kapazitiver Kopplung wächst die
Spannung bei kleinen Frequenzen zunächst wie ω2. Für
sehr große Frequenzen fällt sie auf einen konstanten Wert U0
k/(1+k). Für schwache Kopplung ( k = C'/C << 1) nähert sich
dieser Wert Uo. Die maximale Spannung ist (für kleine Kopplung nur
leicht) zu niederen Frequenzen verschoben.
Verwendet man z.B. C = 1 µF und C' = 0,1 µF, also k = 0,1, ist
ωmax ca. 5 % kleiner als die "Idealfrequenz"
ωo = 1/√(L2·C): ωmax
= ωo·1/√(1 + k). (Der asymptotische Wert der
Schwingkreisspannung ist ca. 9 % der Generatorspannung.)
|
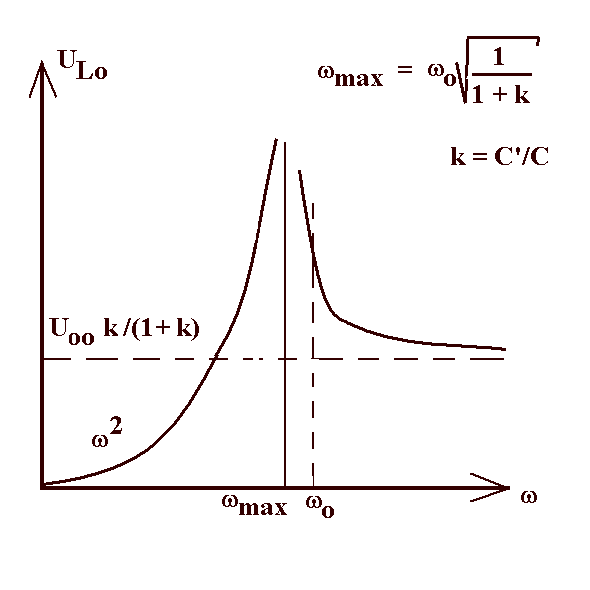 |
| Abb. 4a: Die Resonanzkurve entspricht beim
mechanischen Pendel ebenfalls der Beschleunigungskopplung
(wie beim Seismographen). Vgl. mit Ergebnis der
Theorie. |
|
|
|
|
| Zusammenfassung:
1. Das oft erwünschte Ziel, für die Schule eine maximale
Spannung am Schwingkreis bei einer Kreisfrequenz zu erhalten,
die mit ω0 = 1/√ L2.C übereinstimmt,
lässt sich nur dann erreichen, entweder
a) exakt, wenn reine galvanische Kopplung mittels eines
Widerstands R vorliegt (R sollte dann möglichst groß
sein), oder
b) näherungsweise, wenn die Kopplung sehr schwach ist,
bzw. wenn die Kopplungsgrößen (C') klein sind im Vergleich zu
den entsprechenden Schwingkreisgrößen (C) bzw. wenn L1
>> L2 (Abb. 3). Im Fall der induktiven
Kopplung nach Abb. 1 sollte durch räumlichen Abstand
der zwei Spulen die Gegenkopplung k = M/√ L1·L2
klein gemacht werden.
2. Der unterschiedliche Verlauf der Resonanzkurve hängt von
der Ankopplung des Erregers ab. Je nach Kopplungsart hat die
Resonanzkurve unterschiedliches Verhalten für kleine und sehr
große Kreisfrequenzen ω. Das sollte m.E. in der Schule nicht
diskutiert werden. Für die Schule besteht hier der Ausweg, diese
Grenzfälle nie zu erwähnen, und eine Resonanzkurve nur in der
Nähe der Resonanz zu zeichnen und diskutieren zu lassen. In
Schulbüchern wird in der Regel die falsche Resonanzkurve
zur verwendeten Kopplungsart angegeben.
3. Bei der induktiven Kopplung nach Abb. 3 muss man besonders
vorsichtig sein. ωmax nahe ω0
=
1/√ L2·C erhält man nur, wenn L1
>> L2 !
4. Für die Messung von L mittels der Resonanzfrequenz eines
Schwingkreises ist am besten galvanische Kopplung geeignet, weil
bei ihr die Resonanzfrequenz genau mit der Thomson-Formel
übereinstimmt (bei fehlender interner Dämpfung).
|
Bemerkung: Eine Dämpfung des Schwingkreises durch einen
zusätzlichen internen ohmschen Widerstand ist hier gänzlich
vernachlässigt. Sie führt zu einer zusätzlichen - häufig
geringen - Verschiebung der Frequenz für das Maximum der
Schwingkreisspannung.
Anhänge
A Theoretische Überlegungen zur ersten
Schaltung (Abb. 1; induktive Kopplung):
a) Hier liegen zwei Kreise vor: Kreis 1 mit dem Funktionsgenerator, der
die
Spannung U0(t) = U00 exp
(i(ω t+δ)) liefert
und der Schwingkreis, der die Nummer 2 erhält. Nach der Maschenregel
gilt für Kreis 1:
(1) U0(t) = R·I1 + L1·dI1/dt +
M·dI2/dt
L1·dI1/dt und M·dI2/dt
kommen
durch Selbstinduktion in Kreis 1 und Gegeninduktion von Kreis 2 zustande.
Die eigentlichen Induktionsspannung hätten umgekehrtes Vorzeichen und
hätten links eingeordnet werden müssen. Die Gegeninduktivität
M ist symmetrisch in beiden Induktivitäten (Kreis 1 wirkt auf
Kreis 2 und umgekehrt), also ist der Ansatz M = k
√ L1·L2 üblich,
wobei 0 <= k <= 1 gilt. Mittels der Gegeninduktion wirkt der
Schwingkreis 2 zurück auf den Kreis 1.
(2) 0 = Q2/C + L2·I2*+ M·I1*
(* soll die erste Ableitung nach der Zeit
kennzeichnen).
Wieder spielt die Gegeninduktivität eine Rolle, weil der Kreis 1 auf
den Schwingkreis 2 mit der Gegeninduktion einwirkt. Zeitableitung bewirkt
(2') 0 = I2/C + L2·I** + M·I1**
(**
soll die zweite Ableitung nach der Zeit kennzeichnen).
Es handelt sich um ein gekoppeltes lineares Gleichungssystem mit
konstanten
Koeffizienten. Da wir nicht den Einschwingvorgang beachten wollen, genügt
uns eine spezielle Lösung dieses inhomogenen Gleichungssystems, die
wir durch die Ansätze
I1(t) = I10 · exp(i·ω·t)
und
I2(t) = I20 · exp(
i·ω·t)
erhalten. Der zeitabhängige Faktor fällt dann auf beiden Seiten
der Gleichungen heraus und es folgt:
(1") U00 exp(-iδ) =
i·ω·L1·I10 +
i·ω·M·I20
(2") 0 =
I20 /C -
ω2·L2·I20
-
ω2·M·I10
Wir erhalten: I10 =
I20 ( 1/MCω2 - L2/M ) = I20
L2/M (
1/L2Cω2 - 1) = I20 L2/M
(
ω02/ω2
- 1)
eingesetzt in (1"): U00 exp(-iδ)
= i·ω·L1L2/M
I20 (
ω02/ω2
- 1) +
i·ω·M·I20 also
U00 exp(-iδ) =
i·ω· M·I20 ·[ L1L2/M2 (
ω02/ω2
- 1) + 1 ] = i·ω · M·I20 · [ 1/k2
(
ω02/ω2
- 1) + 1 ]
Die rechte Seite der Gleichung ist rein imaginär, also wegen
exp(-iδ) = cos δ -
i sin δ
U00 sin δ = - I20 · ω · [ L1 (
1/MCω2 - L2/M
) + M ]
Es folgt
cos(δ) = 0 , also
δ = +/-900 und sin
δ = +/-1 , also für den
Betrag /U00/ = / M·I20 ·ω· [
1/k2 (
ω02/ω2
- 1) + 1 ] / und
also I20 = / U00 1/ω
1/(M[ 1/k 2(
ω02/ω2
- 1 ) + 1 ]) /
Damit dann (bis auf das Vorzeichen)
UL0 =
iω·L2·I20 =
iω·L2 · U00 /
(ω·M[ 1/k 2(
ω02/ω2
- 1 ) + 1 ]) =
i·L2·L1/ML1
U00 / [ 1/k 2(
ω02/ω2
- 1 ) + 1 ] =
i √L2/L1 · U00 · k / [ ( ω02/ω2
-
1 + k2 ]
Uns interessiert nur der Betrag davon:
| /UL0/ = √L2/L1 · U00
· k / [ ( ω02/ω2 - 1
+ k2 ] / |
Der Betrag der Schwingkreisspannung ist maximal, wenn der Nenner
verschwindet,
also, wenn
ω02/ω2
= ( 1 - k2)
bzw., wenn ω2 =
ω02 1/(1 -
k2). Das Maximum wird also leicht zu größeren
Frequenzen verschoben.
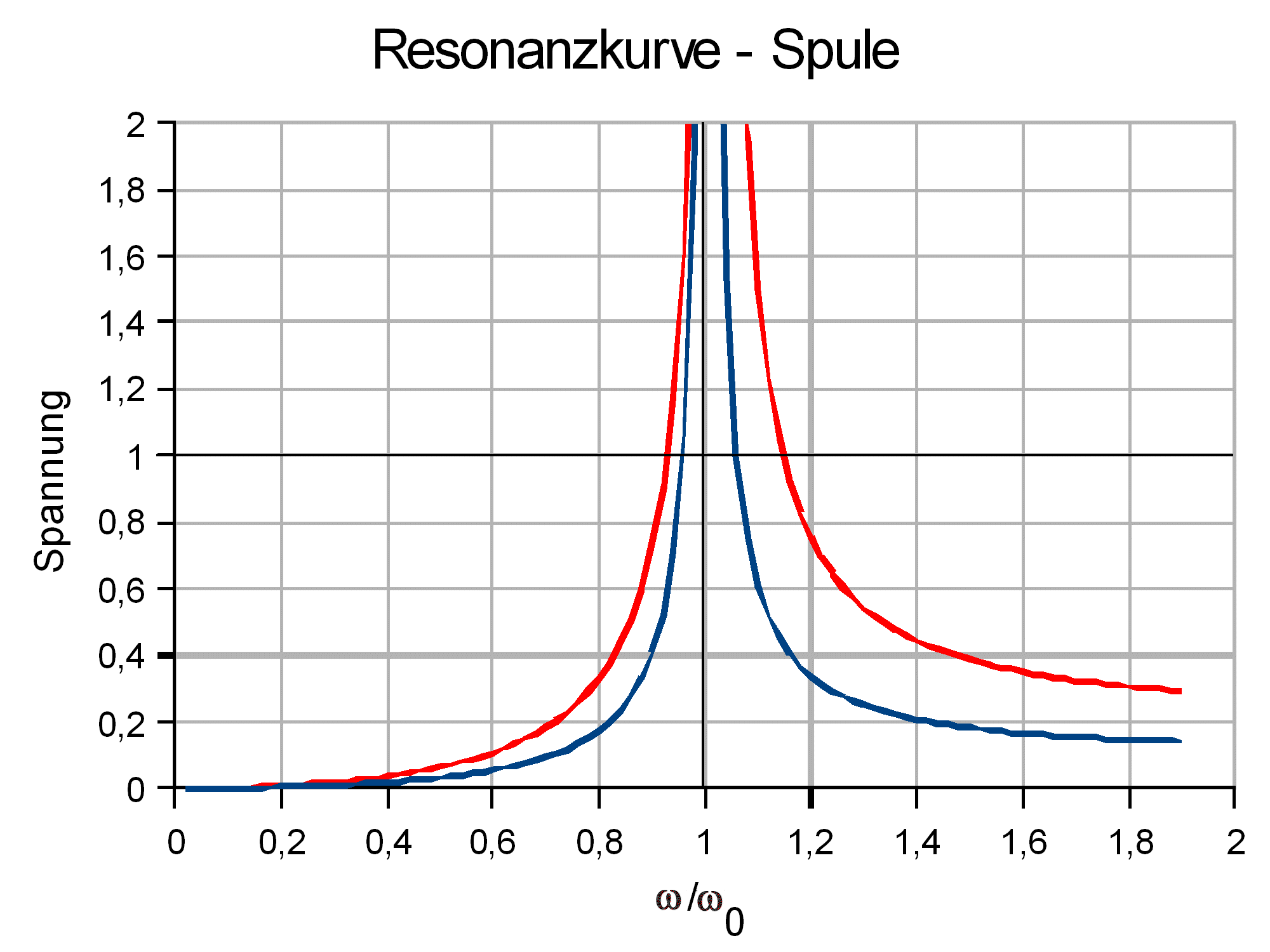 |
Zu Abb. 1, 5: Induktive Kopplung
Für ω => 0 gilt näherungsweise UL0 =
i U00 √L2/L1
k
ω2/ω02 , d.h.,
die Schwingkreisspannung wächst für kleine ω quadratisch
mit ω·
Für ω => unendlich überlebt im Nenner nur (1 - k2),
also gilt näherungsweise /UL0/ = /U00/
√L2/L1 k/ (1 - k2)
Der Betrag von ULO strebt einem konstanten Wert mit
dem Betrag /U00/ √L2/L1 k/
(1 - k2) zu. Nur für sehr kleine k ist dieser
Wert nahezu 0.
Die maximale Schwingkreisspannung kann die Generatorspannung
weit überschreiten.
(blaue Kurve: k = 0,1; rote Kurve k = 0,2; L1 = L2)
|
| Abb. 5: Berechnete Resonanzkurve bei induktiver Kopplung |
|
Anhang B Untersuchung mit komplexen
Widerständen
b) Bei den folgenden Ableitungen sind induktiver Widerstand ZL
= i·ω·L2 und kapazitiver Widerstand
ZC = - i/(ω·C) parallel geschaltet. Wir erhalten für den
komplexen Schwingkreiswiderstand ZS:
1/Zs = 1/(iωL2) +
i ωC = i (- 1 +
ω2 L2C ) /
(ωL2) = i
(ω2/
ω02 - 1) /
(ωL2)
Dieser Widerstand Zs ist in Reihe geschaltet mit ZL1,
R oder ZC'.
|
(1b) Zges = iωL1 +
Zs |
|
(induktiv-galvanisch)
|
| ............... |
(1c) Zges = R + Zs |
...... |
(galvanisch) |
|
(1d) Zges = -i/(ωC') + Zs |
|
(kapazitiv) |
Wenn X der Reihe nach der komplexe Widerstand des jeweiligen
Kopplungsglieds
ist, erhalten wir für die Schwingkreisspannung jeweils
UL = U0 Zs/Zges =
U0/ (1 + X/Zs) = U0/ [ 1 + i·X·(ω2/
ω02 - 1) /
(ωL2) ]
Der Gesamtwiderstand ist in den zwei Fällen (1b) und (1d) rein
imaginär. Sein Betrag kann bei einer bestimmten Kreisfrequenz
ωmax verschwinden. Dort wird
die Amplitude der erzwungenen Schwingung über alle Grenzen wachsen,
wenn ein interner ohmscher Widerstand im Schwingkreis vernachlässigt
wird. Das geschieht, wenn
(1b) /Zges/ = ωL1
+ ωL2
/(ω2/
ω02 - 1) = (
ωL1(ω2/
ω02 - 1) +
ωL2 )
/(ω2/
ω02 - 1) =
ω L1 (
ω2/
ω02 - 1 +
L2/ L1 )/ (ω2/
ω02 - 1) = 0, wenn
also
ω2/ ω02 - 1 +
L2/ L1 bzw. ω2
= ω02 (
1 - L2/ L1) , also, wenn
ωmax = ω0
√ ( 1 - L2/ L1) =
ω0
√1 - 1/k , wobei k =
L1/L2
(1c) /Zges/ = -1/(ωC') +
ωL2
/(ω2/
ω02 - 1) =
ωL2 ( -
C/(ω2C'CL2) +
1/(ω2/
ω02 - 1) =
ωL2 ( - C/C'
ω02/ω2
(ω2/
ω02 - 1) + 1
) / (ω2/
ω02 - 1) = 0 , wenn
also
ω02/ω2
= 1 + C'/C bzw.
ωmax =
ω0 √
1/(1+k) , wobei k = C'/C
Bei galvanischer Kopplung verschwindet der komplexwertige Gesamtwiderstand
an keiner Stelle.
.
1. Fall induktiv-galvanische Kopplung(Abb. 3):
Dann gilt (2b) X = i·ω·L1 und
UL = U0/ [ 1 -
ωL1
(ω2/
ω02 - 1) /
(ωL2) ] = U0/ [ 1 -
L1 /L2 (ω2/
ω02 - 1) ] , also
für den Betrag
| /UL / = / U0/ [ 1 + k - k (ω2/
ω02 ) ] / |
mit k = L1/L2
Maximale Schwingkreisspannung ergibt sich, wenn der Nenner verschwindet,
wenn also 1 + k = k (ω2/
ω02) =>
(ω2/
ω02 ) = 1/k + 1 =>
ω2 =
ω02·(1/k + 1 ) . Wir erhalten also
ωmax
= ω0
√ (1 /k + 1)
Für ω => 0 strebt UL gegen
U0/( (k + 1 ) , UL und U0 schwingen
in Phase. Für ω => unendlich dagegen
verhält sich UL wie - U0 1/k
ω02/ ω2
. UL ist jetzt gegenphasig zu U0 . Der Betrag
fällt mit 1/ω2 gegen 0.
2. Fall kapazitive Kopplung (Abb. 4):
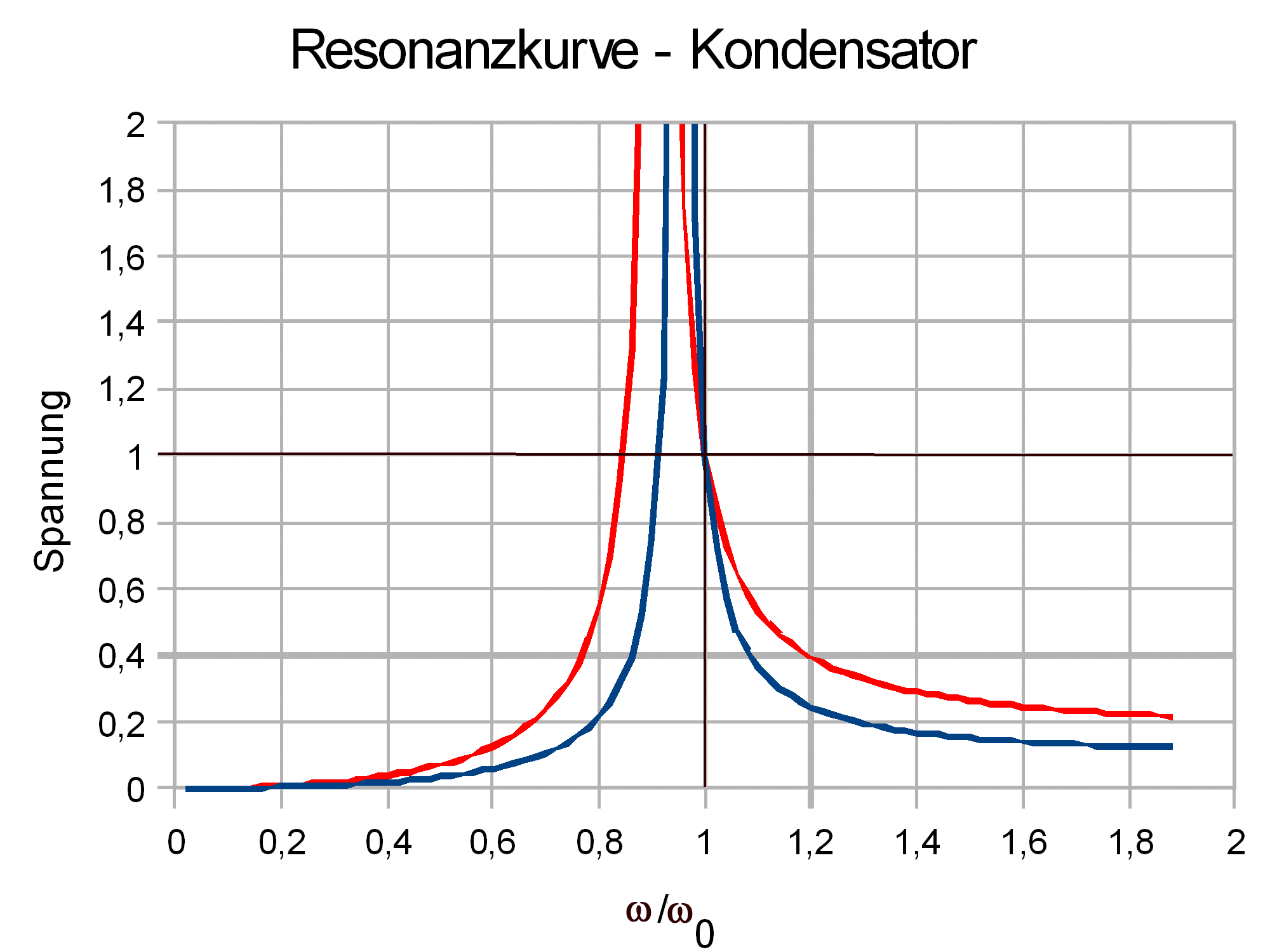 |
Zu Abb. 4, 6: Kapazitive Kopplung
UL = U0/ (1 + i·X·(ω2/ω02
- 1) / (ωL2) ) mit
(2d) X = -i/ωC'
Zur Abkürzung führen wir noch k = C'/C ein. Also:
UL = U0/ (1 + (ω2/
ω02 - 1) / (ω2L2C')
= U0/ (1 + (ω2/ω02 -
1) / (ω2/ ω02 C'/C ) = U0/
(1 + C/C' - ω02/ ω2 C/C')
= U0C'/C / (C'/C + 1 - ω02/
ω2 ), also
| /UL / = /U0 k
/ (1 + k - ω02/ ω2
)/ |
Maximale Schwingkreisspannung ergibt sich, wenn der Nenner
verschwindet, wenn also 1 + k = ω02/ ω2
bzw. ω2 = ω02/(1 +
k), also ωmax = ω0√1/(1 + k). Das Maximum
ist zu kleineren Frequenzen verschoben.
Für ω => 0 verhält sich UL wie - U0
k ω2/ ω02 . UL und
U0 schwingen also gegenphasig. Der Betrag von UL
wächst damit mit ω2.
Für ω => unendlich strebt UL gegen U0
k / (1 + k)
Die maximale Spannung kann die Generatorspannung weit
überschreiten.
(blaue Kurve: k = C'/C = 0,1; rote Kurve k = 0,2)
|
| Abb. 6: Berechnete Resonanzkurve bei kapazitiver Kopplung |
|
3. Fall galvanische Kopplung (Abb. 2):
UL = U0/ (1 + i·X·(ω2/
ω02 - 1) /
(ωL2) ) mit (2c) X = R
Es ergibt sich
UL = U0/ (1 + i R
(ω2/
ω02 - 1) /
(ωL2) ) = U0 / ( 1
+ i R (ω2/
ω02 -
1)/ωL2 mit dem Betrag
/UL/ = /U0 ( 1 +
R2(ω2/
ω02 -
1)2/ω2L22
) -1/2 / = /U0 [
1 + R2/L22
(ω /
ω02 -
1/ω)2 ] -1/2
/ = /U0 [ 1 +
R2C2/(C2L22)
(ω /
ω02 -
1/ω)2 ] -1/2 / , also
| /UL/ = /U0 [ 1 + ω04·
τ2 (ω / ω02
- 1/ω)2 ] -1/2 /
, wobei τ = R·C |
Für ω => 0 verhält sich /UL/
wie /U0/ [
R2/L22 /ω 2
] -1/2 = /U0/ L2 / R
ω = /U0/
ω/(τ·ω02),
wächst also linear mit ω.
Für ω =>unendlich verhält sich
/UL/ wie /U0/ [
R2/L22 (ω
/ ω02 )2 ]
-1/2 = /U0/ L2 / R
ω02 /
ω = /U0/ 1/(
τ·ω ), fällt
also mit 1/ω gegen 0 ab.
Es gibt offenbar keine Stelle, wo der Nenner 0 wird. 1 +
R2/L22 (ω
/ ω02 -
1/ω)2 > 0 . Es könnte
ein relatives Maximum vorliegen. Also:
d/ UL/ dω =
/U0/ (-1/2) [ 1 +
R2/L22 (ω
/ ω02 -
1/ω)2 ] -3/2 · (R2/L22
2
(ω /
ω02 -
1/ω)
(1/ω02 +
ω-2 ) = 0, wenn
ω /
ω02 =
1/ω, bzw.
ωmax 2 =
ω02 .
Durch den Ohmschen Widerstand R ist diese R-L-C-Kombination gedämpft.
Es gibt ein endliches Maximum bei der Eigenfrequenz des Schwingkreises!
Bei kleinem Widerstand zwingt der Funktionsgenerator dem Schwingkreis
seine
Schwingung zu stark auf, und eine Resonanz ist nicht mehr erkennbar.
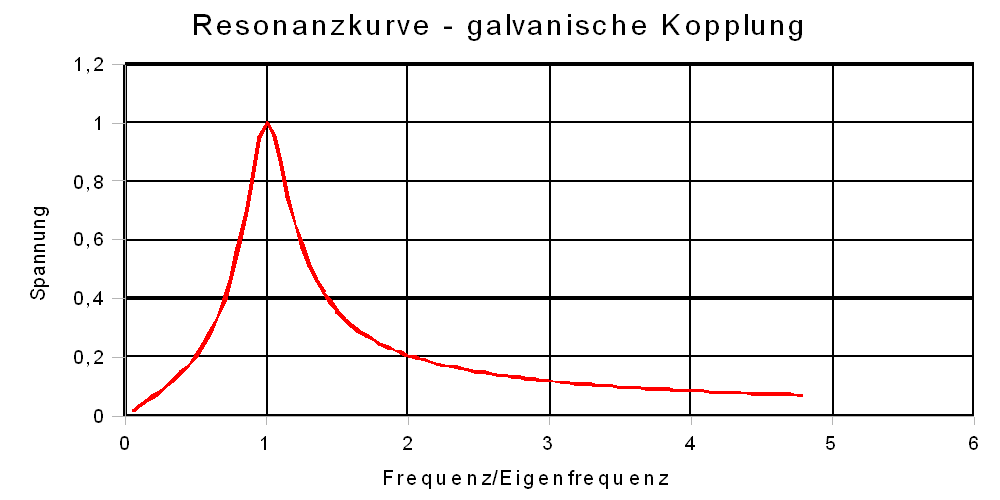 |
Zu Abb. 2, 7: Zwei verschiedene Resonanzkurven
bei galvanischer Kopplung: τ = R·C = 1 ms.
Um eine scharfe Resonanzkurve zu erhalten, sollte der
Schwingkreis möglichst schwach an den Frequenzgenerator
angekoppelt sein: möglichst großer Kopplungswiderstand (hier C =
1 µF, R = 1000 Ohm => τ = 1 ms).
Die maximale Schwingkreisspannung kann die Generatorspannung
nicht überschreiten.
|
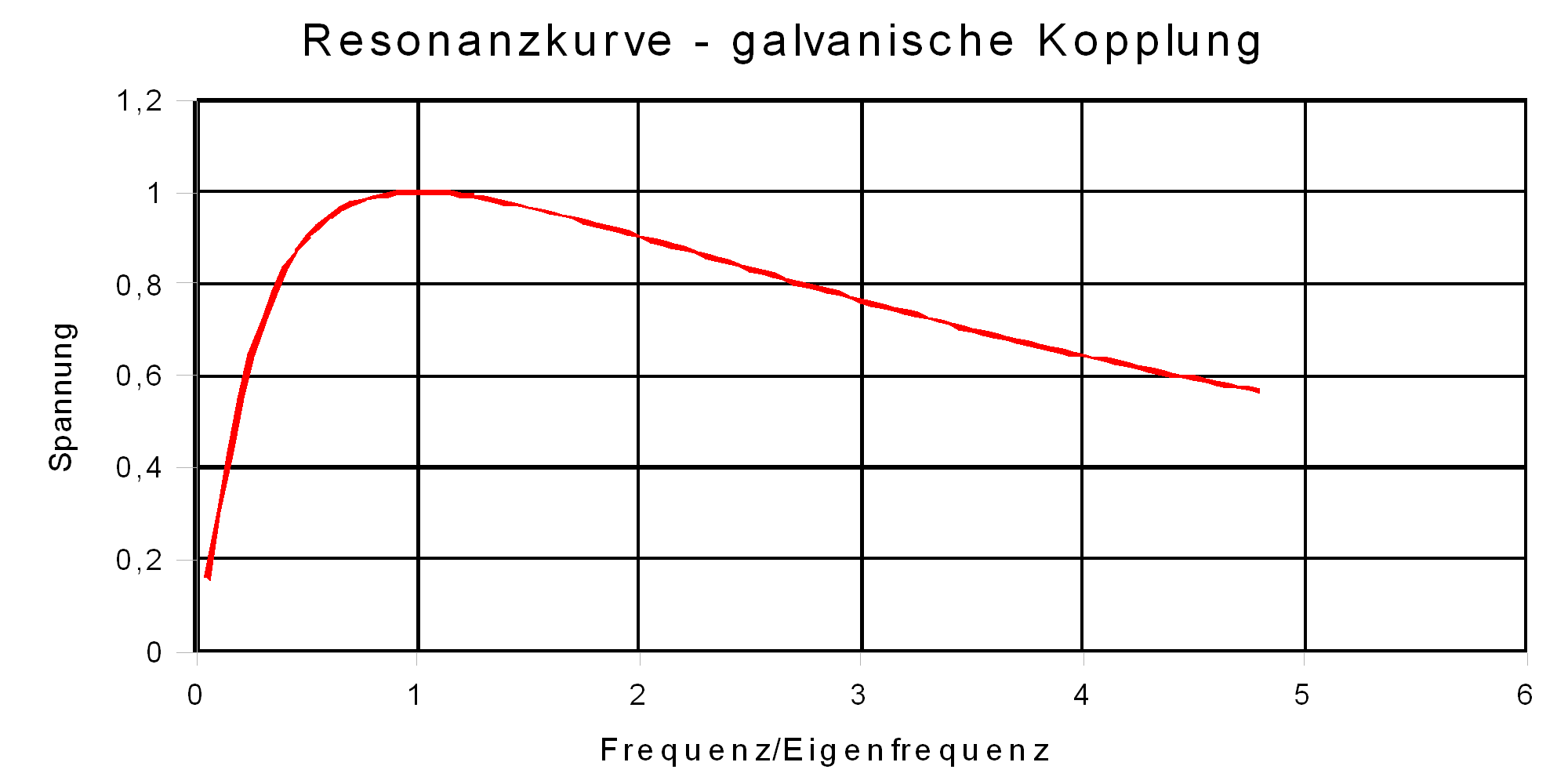 |
τ = 0,1 ms (hier C = 1 µF, R = 100 Ohm => τ = 0,1 ms)
Hier ist der Kopplungswiderstand zu klein. Er entzieht dem
Schwingkreis zuviel Energie. Der Funktionsgenerator zwingt dem
Schwingkreis zu stark seine eigene Amplitude auf.
|
| Abb. 7: Berechnete Resonanzkurven bei galvanischer
Kopplung |
|
C Elementare
Überlegungen
b) Zu Abb. 2, 7 (galvanische Kopplung)
Für kleine Frequenzen strebt der komplexe Widerstand der Spule
iωL2 gegen 0. Es ist also eine kleine
Spannung am Schwingkreis zu erwarten. Die Schaltung wirkt als
Spannungsteiler
und es bildet sich am Schwingkreis eine Spannung
iωL2 / (R + i
ωL2 ) aus. Der Betrag ist
U0ωL2
1/√(R2
+ ω2L2
2) =
U01/√(R2
/ ω2L2
2 + 1).
Für ω =>0 ist die 1 im Nenner
vernachlässigbar und UL0 verhält sich wie U0
ωL2/R, wächst also mit
ω linear an.
Für sehr große ω dagegen verhält
sich die Schaltung wie eine Spannungsteilerschaltung von R und
-i/ωC. /UL0/ verhält sich
also wie U0
1/ωC/√(R2+1/ω2C2)
= U0
1/√(R2ω2C2
+ 1 ) = U0 1/(RωC), strebt also
wie 1/ω gegen 0.
c) Zu Abb. 3, 5 (induktiv-galvanische Kopplung):
Bei kleinen Frequenzen ist der kapazitive Widerstand von C sehr groß
im Vergleich zu den induktiven Widerständen von L1 und
L2. De facto liegt für kleine Frequenzen eine
Spannungsteilerschaltung mit zwei Spulen vor. Die Eingangspannung
U0 wird im Verhältnis von
ωL2/ω(L1+L2)
= 1/(1+k) (k = L1/L2): horizontale Asymptote
bei dieser Spannung.
Bei sehr großen Frequenzen ist im Schwingkreis der kapazitive Widerstand
-i/ωC sehr klein im Vergleich zum induktiven
Widerstand iωL2. Es gilt wieder das
Argument der Spannungsteilerschaltung. Am Schwingkreis entsteht eine
Spannung
U0 -i/ωC /
iωL1= U0
ω02 /
ω2 L2/L1 . Die
Schwingkreisspannung fällt wie 1
/ω2 auf 0.
d) Zu Abb. 4, 6 (kapazitive Kopplung):
Bei großen Frequenzen überwiegt der induktive Widerstand iωL2
der Schwingkreisspule. Die
Spannungsteilerschaltung besteht aus den kapazitiven Widerständen
-i/ωC' und -i/ωC. Es
bildet sich eine Schwingkreisspannung aus, die sich bei großen Frequenzen
verhält wie U0 1/C / (1 /C + 1/C') = U0 C'/( C
+ C') = U0 k/(1 + k ), wobei k = C'/C.
Bei sehr kleinen Frequenzen dominiert der kleine induktive Widerstand
iωL2 den Schwingkreiswiderstand.
UL0 verhält sich wie U0
iωL2 / (
iωL2 -i/ωC')
= U0 L2 / ( L2
-1/ω2C'). Der Betrag davon verhält
sich wie U0 L2
ω2C' = U0 L2C
ω2 C'/C = U0
ω2/ω02
C'/C , wächst also mit
ω2.
.
.
.
.
( Sonderzeichen korrigiert, Überschriften eingefügt 2014)
( März 2016 : Formatierungsfehler beseitigt )
 ´
´