|
Elektromagnetische Induktion
|
Überprüft, ergänzt, aber immer noch unvollständig
1. Historisches
Oersted hat Anfang des 19. Jahrhunderts gefunden: "Elektrizität
macht Magnetismus" (Ein elektrischer Strom umgibt sich mit einem
ringförmig geschlossenen Magnetfeld). Michael Faraday spekulierte
wenige Jahrzehnte später: Könnte auch gelten "Magnetismus macht
Elektrizität"? Das sieht nach einer Umkehrung aus.
2. Im Schülerversuch entdeckst du die Induktion
 |
Auf eine Spule mit 12 000 Windungen ist eine
Zweifarben-Leuchtdiode aufgesetzt. Je nach Stromrichtung leuchtet
sie rot oder grün. Versuche, sie mit dem Magneten zum Leuchten zu
bringen.
Im Foto leuchtet sie grün; sie kann aber bei diesem Vorgang
auch rot leuchten!?
Lässt sich eine Regel ableiten, wann die Leuchtdiode überhaupt
leuchtet? Wann sie in der einen oder der anderen Farbe leuchtet?
Wann sie besonders hell leuchtet?
Wenn die Leuchtdiode Energie in Form von Licht abgibt, muss
diese von irgendwo her kommen. Hast du eine Idee, wer dann
Arbeit verrichtet, Energie hineinsteckt?
|
 |
In einer Variante ist hier ein kleiner Strommesser auf die Spule
mit 300 Windungen aufgesetzt. Wie oben wird gefragt:
Lässt sich eine Regel ableiten, wann das Messgerät überhaupt
ausschlägt? Wann es nach rechts oder nach links ausschlägt? Wann
es besonders stark ausschlägt?
|
Ganz so einfach, wie sich Faraday das ursprünglich vorgestellt hatte,
sind die Verhältnisse hier wohl nicht: Mit Magnetismus lässt sich
tatsächlich Elektrizität erzeugen, aber wann nur? Ein Magnet kann noch so
stark sein; wenn er nur im Inneren der Spule ruht, kommt es nicht
zur Induktion!
3. Wann entsteht Induktion?
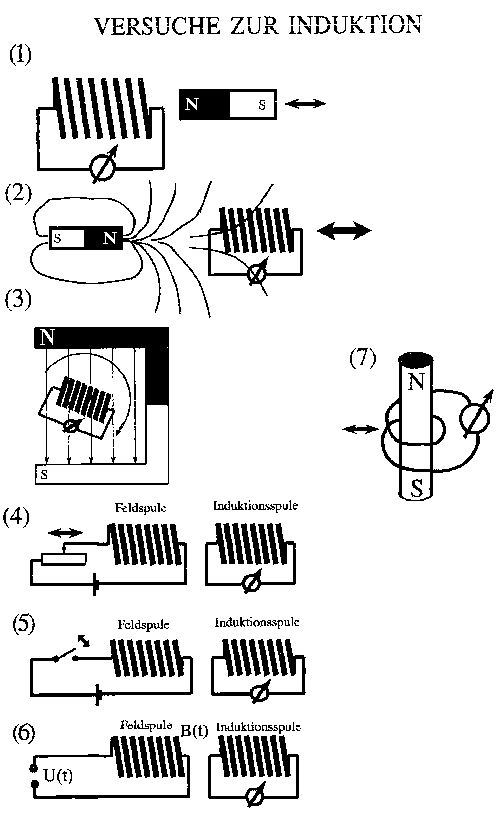 |
In der "Bildergeschichte" links sind verschiedene Versuche
bildlich dargestellt, bei denen Induktion entsteht. Die
Situationen sind z.T. völlig unterschiedlich; dennoch haben sie
etwas Wesentliches gemeinsam.
Führe die Versuche durch oder vergleiche mit dem Experiment,
das der Lehrer durchführt. Das Wesentliche für die Entstehung
der Induktion ist in allen Fällen angedeutet. Versuche, es zu
erkennen. Formuliere dann in dein Heft zu jedem der Versuche
zwei Sätze nach dem Schema:
| 1. Induktion entsteht in Situation xy [(1), oder
(2), ... ], weil ....
2. Das geschieht dadurch, dass ...
|
Im 2. Satz geht es konkret darum, was hier gemacht wurde. Der
1. Satz dagegen sollte das allen Versuchen Gemeinsame enthalten.
Einige Textbausteine könnten sein:
- ändert sich
- Magnetfeld
- das die Windungsfläche senkrecht durchsetzt
- Windungsfläche
- homogenes / inhomogenes
- ...
Die Feldspule heißt so, weil durch sie bei Stromfluss
ein Magnetfeld erzeugt wird. Die Induktionsspule
heißt so, weil bei ihr bei Funktionieren des Versuchs Induktion
mit einem Messinstrument (Strom- oder Spannungsmesser)
nachgewiesen werden kann.
Beispiel:
1. Induktion entsteht in Situation (1), weil sich in
der Spule das Magnetfeld ändert, das die
Spule senkrecht durchsetzt.
2. Das geschieht dadurch, dass der Permanentmagnet der Spule
angenähert oder von ihr entfernt wird. (Das Magnetfeld, das er in
der Spule erzeugt, wird größer bzw. kleiner.)
Gehe bei deinen Formulierungen immer von
der Induktionsspule aus. Setze dich sozusagen in sie hinein
und betrachte, was mit dem Magnetfeld in ihrem Inneren (von
diesem Standpunkt aus) geschieht.
|
Die Situation (7) unterscheidet sich von den Situationen (1) - (6). In
der Situation (7) stellst du fest: Induktion findet auch statt, wenn sich
die "Menge an Magnetfeld" ändert, die die Windungsfläche senkrecht
durchsetzt, indem die Windungsfläche vergrößert oder verkleinert wird.
Kompakt kann man alle Situationen beschreiben, wenn man den Begriff des
"magnetischen Flusses" einführt. Der magnetische Fluss enthält
Informationen über die Stärke des Magnetfelds (B), das die
Windungsfläche senkrecht durchsetzt, und die Windungsfläche A selbst.
Später wirst du erfahren: Wenn B der Anteil des Magnetfelds
ist, der die Windungsfläche A senkrecht durchsetzt, gilt Φ = B·A .
Zusammenfassend kann man also alle 7 Situationen beschreiben:
| Induktion findet in einer Spule oder geschlossenen
Leiterschleife statt, wenn sich in ihr
der "magnetische Fluss" ändert.
Das könnte geschehen, wenn sich die Stärke des Magnetfelds B
ändert, das die Windungsfläche senkrecht durchsetzt, oder
die "Menge an Magnetfeld", die von der Windungsfläche
umfasst wird, also z.B. die Größe der Windungsfläche A
selbst. |
Du siehst: Die Idee von der "Umkehrung", von der anfangs die Rede war,
war sehr erfolgreich, indem sie zur Entdeckung der Induktion führte. Aber
um eine echte Umkehrung handelt es sich nicht: Es musste die zeitliche
Änderung ins Spiel gebracht werden.
.
4. Was entsteht bei der Induktion?
Zur Anzeige wurde eine Leuchtdiode, ein Strommesser oder ein
Spannungsmesser verwendet. Auch ein empfindliches Glühlämpchen hätte
manchmal verwendet werden können. Offenbar fließt bei den Versuchen immer
ein Strom. Ist das aber die direkte (primäre) Wirkung der Induktion? Klar
ist, wenn ein Strom entsteht, könnte er eine Ursache haben, die so etwas
wie eine Spannung sein könnte. Umgekehrt, wenn primär eine
Induktionsspannung entsteht, hat sie in einem geschlossenen Stromkreis
sicher sekundär einen Strom zur Folge. Wir fragen hier also, was als
Erstes da war, so etwas wie eine Spannung oder ein Strom?
Versuche:
V1: Primärspule mit Eisenkern, Sekundärspule. Durch die
Primärspule fließt ein langsam linear anwachsender oder abfallender Strom.
In der gleichen Weise verändert sich auch das Magnetfeld in der
Primärspule. Die Sekundärspule wird nacheinander durch unterschiedliche
Widerstände zu einem Stromkreis geschlossen, der einen Strommesser
enthält.
E: Trotz jeweils gleicher Ursache der Induktion (der zeitlichen
Änderung des magnetischen Flusses) entstehen unterschiedliche
Stromstärken, je nach Widerstand im Stromkreis.
| Bei der Induktion entsteht primär kein Induktionsstrom.
Dieser ist die Folge von etwas anderem. |
 |
V2: Über den Eisenkern der Primärspule wird eine
Sekundärspule aus einer Windung gestülpt. Sie enthält einen
empfindlichen Spannungsmesser. Das Magnetfeld in der Primärspule
und im Eisenkern ändert sich wie oben.
E1: Ganz gleich, wie die Windung um den sich ändernden
magnetischen Fluss gelegt wird (wenn nur die Windungsfläche
senkrecht dazu bleibt), es wird die gleiche Spannung angezeigt.
E2: Es gibt nirgendwo einen Plus- und einen Minuspol
(wohl aber eine zeitabschnittsweise eindeutige Richtung des
Ringstroms).
|
 |
V3: Verschärfung durch elektrodenlose Ringentladung:
Eine mit Neongas gefüllte Kugel wird von einer Spule aus wenigen
Windungen umgeben. Sie ist Teil eines elektromagnetischen
Schwingkreises, mit dem ein Wechselstrom (und damit ein
magnetisches Wechselfeld) sehr hoher Frequenz erzeugt wird. Im
Inneren der Neonkugel beginnt das Gas zu leuchten, und zwar in
einem Ring senkrecht zur Windungsfläche der Spule. Es entsteht ein
Ringstrom ohne Anfang und Ende.
(Er ist die Folge eines starken elektrischen Felds,
das die magnetischen Feldlinien ringförmig senkrecht umfasst.
Das starke elektrische Feld macht das Neongas leitfähig.)
| E3: Es entsteht primär so etwas wie eine
Spannung, aber keine gewöhnliche Spannung (keine
Potenzialdifferenz):
Von keinem Punkt längs der
ringförmigen Induktionsschleife in V2 kann
behauptet werden, dass er das höchste oder
niedrigste Potenzial im Vergleich zu seinen
Nachbarn hätte: Es gibt bei der Induktion kein
Potenzial und keine Potenzialdifferenz.
|
|
V4: Hätte man im Versuch V2 für äußerlich gleiche
Leiterschleifen Materialien mit unterschiedlichen Widerständen verwendet,
hätte sich mit einem eingebauten hochohmigen Spannungsmesser immer die
gleiche Induktionsspannung ergeben, mit einem eingebauten Strommesser je
nach Leiterwiderstand unterschiedliche Stromstärken.
| E4. Primär entsteht eine Induktionsspannung,
die sekundär einen Induktionsstrom zur Folge hat, der ohne Anfang
und Ende im Kreis herum fließt (Ringstrom ohne Plus- und
Minuspol), und dessen Größe von der Induktionsspannung und vom
Leiterwiderstand abhängt. |
Die Induktionsspannung ist ein Spezialfall einer "Ringspannung".
Manchmal wird sie auch "Umlaufspannung" genannt.
.
.
5. Was ist eine Ringspannung?
Im allgemeinen hat die Leiterschleife einen Widerstand, vielleicht einen
sehr kleinen. Um durch ihn den Ringstrom hindurchzupumpen wird Arbeit
benötigt, auch dann, wenn der Strom vom Punkt A durch den Leiterkreis (um
den sich ändernden magnetischen Fluss herum) wieder zum Punkt A
hindurchgepumpt wird. Das ist offenbar ganz anders als bei einem
Potenzialfeld wie in einem Plattenkondensator. Bei einem geschlossenen Weg
von einem Punkt A zum Punkt A zurück muss dort auf Teilwegen Arbeit
verrichtet werden, die auf anderen Teilwegen wieder gewonnen wird, so dass
insgesamt bei einem vollen Umlauf keine Arbeit verrichtet wird. Bei
der Induktion dagegen wird bei jedem vollen Umlauf Arbeit verrichtet.
In einem Potenzialfeld wird zwischen zwei Punkten A und B eine Spannung
UAB definiert durch UAB = WAB/Q, wenn WAB
die Arbeit ist, die zum Transport der Ladung Q von A nach B aufgewendet
werden muss.
Ganz entsprechend wird die Ringspannung UO
definiert, die bei der Induktion entsteht: UO = W/Q.
Dabei ist W die Arbeit, die beim Transport der Ladung Q auf einem
geschlossenen Weg aufgewendet werden muss. (Das Symbol O
soll dabei die Ringspannung längs des geschlossenen Wegs
andeuten.). Weil die Ringspannung gleichartig definiert ist wie die
gewöhnliche Spannung (Potenzialdifferenz) hat sie auch die gleiche
Einheit: 1 V. (Um das Vorzeichen von UO wollen wir uns hier
nicht kümmern.)
| Bei der Induktion entsteht in allen Fällen längs einer
ringförmig geschlossenen Induktionsspule oder Leiterschleife eine
Ringspannung UO und in der Regel keine
gewöhnliche Spannung. Die Folge dieser Ringspannung ist ein
Ringstrom. |
Bei einer Induktionsspule aus n Windungen muss pro Windung eine
bestimmte Arbeit bzw. Ringspannung aufgewendet werden. Die gesamte
Ringspannung UAA ist also das n-fache dieser Ringspannung pro
Windung. Die einzelnen Windungen sind sozusagen hintereinander geschaltet.
.
.
6. Änderungen des magnetischen Flusses, auch wenn
man sie nicht erwartet
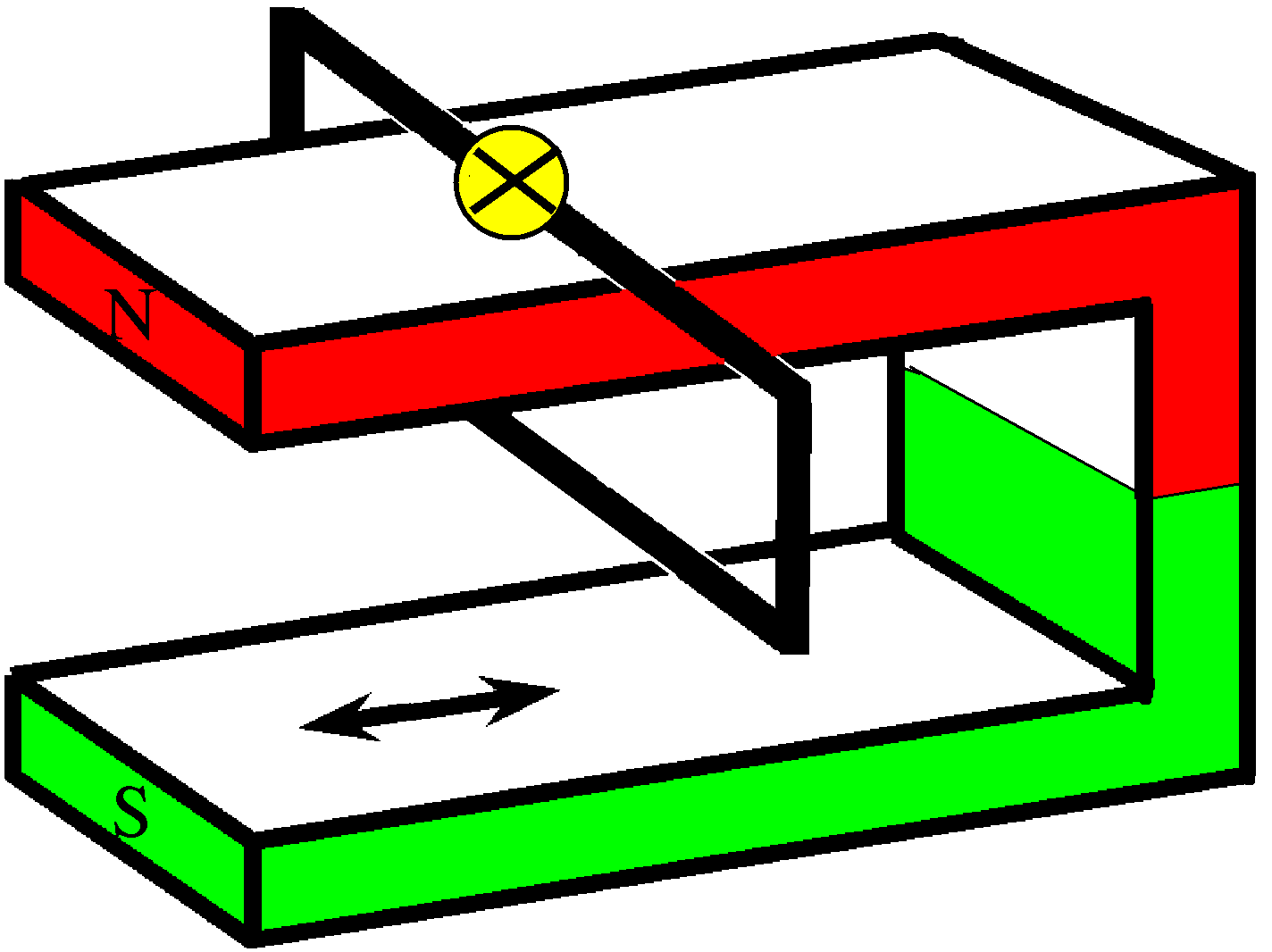 |
Betrachte einen Hufeisenmagneten, dessen einer Schenkel
durch einen rechteckigen gut leitenden Ring gesteckt wird. Der Ring
ist irgendwie fest mit dem Labortisch verbunden.Wird bei ortsfestem
Ring der Magnet hin und her bewegt, also längs des
Schenkels in Pfeilrichtung, entsteht eine Induktionsspannung.
In der Schemazeichnung wird diese durch ein
Lämpchen nachgewiesen, im Realversuch ersetzt man das Lämpchen
durch einen empfindlichen Spannungsmesser.
|

Ganz entsprechend beim Leiterschaukel-Versuch
|
Nach unseren bisherigen Erfahrungen müsste doch auch hier eine Änderung
des magnetischen Flusses stattfinden. Aber was hältst du von folgender
Argumentation:
a) In brauchbarer Näherung kann man sich vorstellen, dass das Magnetfeld
allein auf den Bereich zwischen den Schenkeln beschränkt ist. Dort wird
üblicherweise ein homogenes Magnetfeld angenommen. Es hat also überall
zwischen den Schenkeln gleichen Betrag und gleiche Richtung. Drei Seiten
des Rings befinden sich dann außerhalb des Magnetfelds, die vierte Seite
im homogenen Feldbereich. Diese Seite "verspürt" immer das gleiche
Magnetfeld. Von einer Bewegung des Magneten "bemerkt" sie allein auf Grund
des Magnetfelds gar nichts.
b) Wo sollte hier eine Änderung des magnetischen Flusses
stattfinden? Drei Seiten befinden sich außerhalb des Magnetfelds; dort
gibt es nie ein Magnetfeld. Die vierte befindet sich im homogenen
Feldbereich; dort verändert sich das Magnetfeld nie. Ohne Änderung des
magnetischen Flusses innerhalb der Induktionsschleife keine Induktion!?
Zur Lösung: Du hast sicher nicht übersehen,
dass auch in den Schenkeln des Hufeisenmagneten ein magnetisches Feld
vorhanden ist:
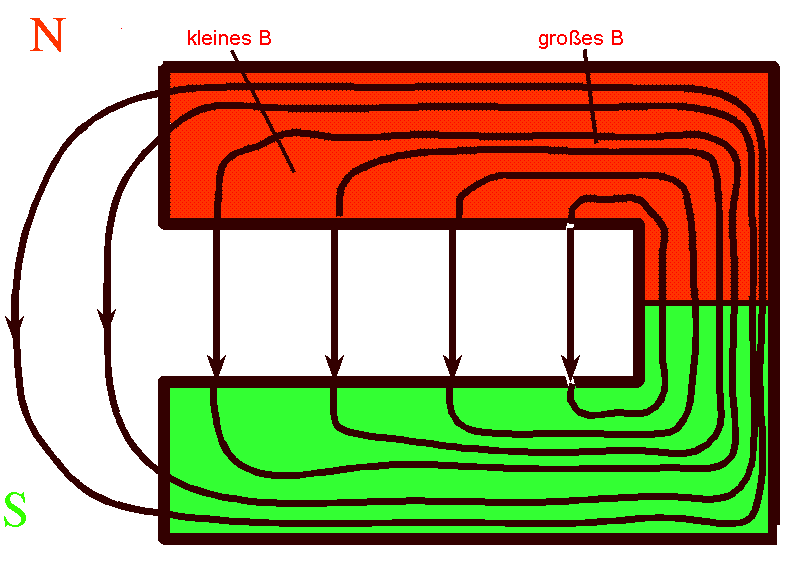 |
Bewegt sich der Hufeisenmagnet hin und her, durchstoßen Feldlinien
im Schenkel die Windungsfläche, einmal viele, einmal
wenige, je nach der momentanen Position des Magneten im Vergleich
zum Ring. Ganz klar: Vom ruhenden Ring aus beurteilt ändert sich in
seiner Windungsfläche der magnetische Fluss, wenn sich der
Hufeisenmagnet bewegt, und zwar im Inneren des Rings, dort wo die
Feldlinien im Inneren des Schenkels die Windungsfläche durchstoßen.
|
Auch in diesem Fall findet Induktion statt, weil sich der magnetische
Fluss, der die Windungsfläche senkrecht durchsetzt, ändert.
.
.
7. Das allgemeine Induktionsgesetz mit dem
Dreiecks-Generator erarbeitet
Ein Dreiecks-Generator ist ein Gerät, das abwechselnd einen linear
wachsenden und dann wieder linear fallenden Strom bzw. eine entsprechende
Spannung erzeugt. Die Frequenz des Dreiecks-Signals lässt sich einstellen,
u.U. bis zu Frequenzen von 0,1 Hz herab. Nach 10 s wiederholt sich in
diesem Fall jeweils der dreiecksförmige Stromverlauf.
 |
Mit dem orangefarbenen Funktionsgenerator wird ein linear
veränderlicher Strom geringer Frequenz durch die Feldspule
(rechts, 600 Windungen) erzeugt. Die Spannung an der
Induktionsspule (links, 12 000 Windungen) wird mit einem
Messinterface (schwarz) gemessen. Der PC stellt den magnetischen
Fluss (linear veränderlich) und die Induktionsspannung dar. Wenn
der magnetische Fluss linear wächst oder fällt, ist die
Induktionsspannung konstant. Das Minuszeichen im Induktionsgesetz
kann hier nicht erkannt werden.
(Messung und Anzeige mit dem PC-Programm URI)
Magnetische Wechselfelder von Transformatoren im Raum
(z.B. im Netzteil des PCs) und Rundfunksendern führen
ebenfalls zu Induktionsspannungen. Sie werden mit dem
parallelgeschalteten blauen Kondensator (Steckerbauteil unten)
weitgehend kurzgeschlossen.
|
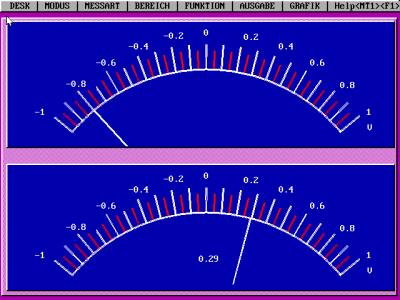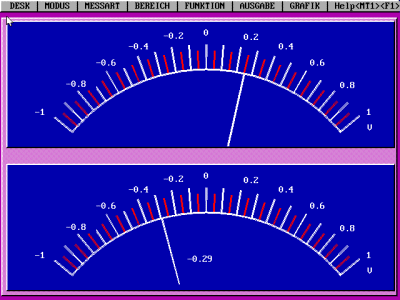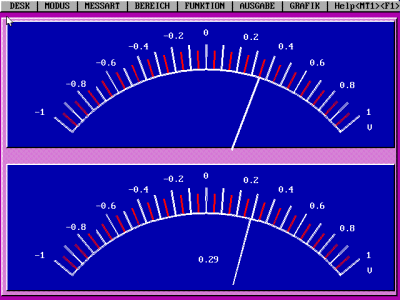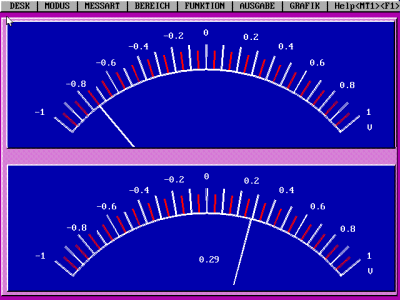 |
Versuchsergebnis:
Der Strom durch die Feldspule (und damit der magnetische Fluss)
wächst linear und fällt periodisch. Die zweite Anzeige
entspricht der Induktionsspannung der Induktionsspule. Was fällt
dir auf? (Messung mit dem PC-Programm URI und einem
Messinterface)
|
Versuche zeigen:
 |
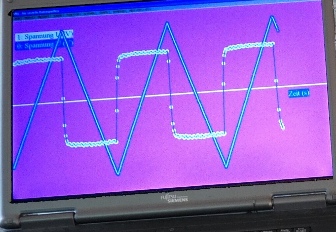 |
| Wie oben. Der PC stellt magnetischen Fluss (dreiecksförmig) und
Induktionsspannung (abschnittsweise konstant) graphisch dar. Wenn
der magnetische Fluss linear wächst, ist die Induktionsspannung
konstant. Das Minuszeichen im Induktionsgesetz kann hier nicht
erkannt werden.
(auch hier: Messung und Anzeige mit dem PC-Programm URI und
einem Messinterface im schwarzen Gehäuse)
|
Gleiche Situation wie links. Nur die Frequenz bzw. die
Änderungsgeschwindigkeit des magnetischen Flusses ΔΦ/Δt
wurde verdoppelt. Welche Folge hatte das für die
Induktionsspannung, die wieder abschnittsweise weitgehend konstant
ist ? |
Hier einige Fotos mit z.T. sehr alten konventionellen Geräten:
|
|
Untersuchung der Zeitabhängigkeit der Induktionsspannung:
Links der Dreiecksstrom-Generator, dessen Ausgangsstrom durch das
große Messinstrument angezeigt wird, die Feldspule (300 - 1200
Windungen), dann die Induktionsspule (12000 Windungen), rechts der
Messverstärker mit relativ trägheitsarm arbeitendem mechanischem
Anzeigeinstrument.
Variiert man die Windungszahl n der Induktionsspule (im Bild
links von der Feldspule), so findet man:
Die (abschnittsweise konstante) Induktionsspannung ist auch
proportional zur Windungszahl n.
Das hatten wir uns aber auch schon theoretisch überlegt, weil bei
größerem n mehr Windungen hintereinander geschaltet sind.
|
|
|
|
Auch die Abhängigkeit der Induktionsspannung von der
Windungsfläche A der Induktionsspule kann mit dem
dreiecksförmigen Magnetfeld untersucht werden. Man muss
allerdings dafür sorgen, dass das Magnetfeld über die
gesamte Windungsfläche (räumlich) konstant ist. Hier wird
das über einen großen Flächenbereich homogene Magnetfeld
durch das Helmholtz-Spulenpaar von der e/m-Bestimmung
erzeugt. In der Symmetrieebene zwischen beiden Ringspulen
ist dort ein homogenes Magnetfeld garantiert. Auf dem
Ständer in der Mittelebene sind mehrere Induktionsspulen
(300 Windungen) unterschiedlicher Windungsflächen A angebracht.
An ihrem Ausgang ist der Messverstärker oder ein
Messinterface angeschlossen.
Der Versuch zeigt:
Die (abschnittsweise konstante) Induktionsspannung ist
auch proportional zur Windungsfläche A.
Das gilt dann, wenn A die vom Magnetfeld senkrecht
durchsetzte Windungsfläche ist. Würde man die
Induktionsspule schräg ins Magnetfeld stellen, wäre die
vom Magnetfeld senkrecht durchsetzte Fläche kleiner, und
damit auch die Induktionsspannung.
Die Helmholtz-Spulen oder andere
(entsprechend Abb. 1a) können bei der Untersuchung der
Abhängigkeit von der Windungszahl auch als
Feldspulen verwendet werden, wenn in das Magnetfeld
beliebige Induktionsspulen gleicher Querschnittsflächen
mit unterschiedlichen Windungszahlen gelegt werden.
|
|
Wir fanden also bisher UO prop. n · ΔB/Δt · A . Jemand
kam einmal auf die Idee aus B und A eine neue Größe zu definieren, den
"magnetischen Fluss" Φ = B · A. A ist dabei immer der Anteil der
Windungsfläche senkrecht zu B (bzw. B die Komponente des
Magnetfelds B senkrecht zur gesamten Windungsfläche. Damit heißt
dann das Induktionsgesetz in der bisherigen Form: UO prop. n ·
ΔΦ/Δt .
Δ Φ/Δt ist die "Änderungsrate" des magnetischen Flusses. Sie gibt an,
wie schnell sich der magnetische Fluss Φ pro Zeiteinheit Δt ändert. Je
schneller sich der magnetische Fluss ändert, der die Induktionsspule
senkrecht durchsetzt, desto größer ist der Betrag der Induktionsspannung.
Deswegen wird ΔΦ/Δt auch "Änderungsgeschwindigkeit" des magnetischen
Flusses genannt.
Bei der Formulierung der gewöhnlichen Geschwindigkeit v hast du
vielleicht kennengelernt, dass bei beliebigen Ortsänderungen (gleichförmig
oder nicht) der Bruch Δx/Δt durch die zeitliche Ableitung v = x·
bzw. v = dx/dt ersetzt werden sollte. Wenn du die Ableitung noch
nicht kennst, genügt es vorläufig, diese Ausdrücke als Abkürzung für Δx/Δt
anzusehen.
(x· wird gelesen als "x punkt",
ähnlich wie im Mathematikunterricht f '(x) für die Ableitung nach x
steht).
Genauso kannst du bei der Änderungsgeschwindigkeit des magnetischen
Flusses vorgehen: ΔΦ/Δt wird ersetzt bzw. abgekürzt durch Φ·
bzw. dΦ/dt. Vollständig formuliert heißt das Induktionsgesetz:
| Allgemeines Induktionsgesetz:
Wenn sich in einer geschlossenen Kurve C der magnetische Fluss Φ
ändert, entsteht längs dieser Kurve C eine Ringspannung UO,
und es gilt:
| UO
= - n · Φ· |
wobei Φ = B·A
|
mit der magnetischen
Flussdichte B und der Windungsfläche A, die von B
senkrecht durchsetzt wird. |
Dabei ist n die Windungszahl und Φ· die
zeitliche Ableitung des magnetischen Flusses Φ, also die
Geschwindigkeit, mit der sich der magnetische Fluss Φ innerhalb
von C ändert. (Im Fall eines linear veränderlichen Flusses mit Φ·
= ΔΦ/Δt (das ist in diesem Fall exakt) hieße das
Induktionsgesetz also:
( Φ· wird gelesen " Fi punkt"; ·
sollte ein hochgestellter Punkt sein)
|
Das Induktionsgesetz gilt ganz allgemein. Es ist keine Form der
Induktion bekannt, die sich nicht auf eine Änderung des magnetischen
Flusses zurückführen lässt. Ein überraschendes Beispiel wurde ja
schon früher diskutiert.
Ein Beispiel: in 1 s ändere sich die magnetische Flussdichte B um
1 V· s/m2. Die Windungsfläche, die vom
Magnetfeld senkrecht durchsetzt wird, sei 10 cm2 = 0,01 m2.
Die Windungszahl n sei 100. Dann gilt also UO = - n · ΔΦ/Δt = -
100 · 1 V· s/m2 · 0,01 m2 / 1 s = 1
V. Die Änderungsgeschwindigkeit des Magnetfelds war dabei ΔB/Δt = 1 V·
s/m2 / 1 s = 1 V/m2 .
.
Hinweis: Zunächst folgt aus dem Experiment
UO prop. ΔΦ/Δt (der
Änderungsgeschwindigkeit des magnetischen Flusses) und UO
prop. n (der Windungszahl) , zusammengefasst also UO
prop. n · ΔΦ/Δt.
Zwei Dinge sind dann zu klären: Warum hat die Proportionalitätskonstante
den Betrag 1? Zweitens, warum enthält das Induktionsgesetz ein negatives
Vorzeichen?
Punkt 1) wird später bewiesen.
Zu 2): Das Vorzeichen ist in vielen Fällen nicht wichtig.
(Wenn außer der Induktionsspannnung keine weitere Spannung
vorliegt, könntest du das Vorzeichen der Spannungsanzeige leicht ändern,
indem du die beiden Anschlüsse des Spannungsmessers vertauschst.)
Es ist aber auch sehr schwierig zu entscheiden , weil es eine
sorgfältige Definition des magnetischen Flusses voraussetzt und nur im
Vergleich zu einer anderen Spannung bedeutsam wird. Manche Schulbücher
machen es sich dabei etwas zu leicht. Im Augenblick solltest du das
negative Vorzeichen einfach glauben. Es bewährt sich z.B. im
Kapitel Selbstinduktion. Dort gibt es nämlich eine Situation, wo ein
ansteigender Strom durch eine Spule durch die Induktionsspannung
zunächst unterdrückt wird. Sie muss also umgekehrtes Vorzeichen haben
wie die Batteriespannung, die den Strom fließen lässt. Wenn der
magnetische Fluss anwächst ( Δ Φ/Δt
> 0 ), ist die entstehende Induktionsspannung negativ.
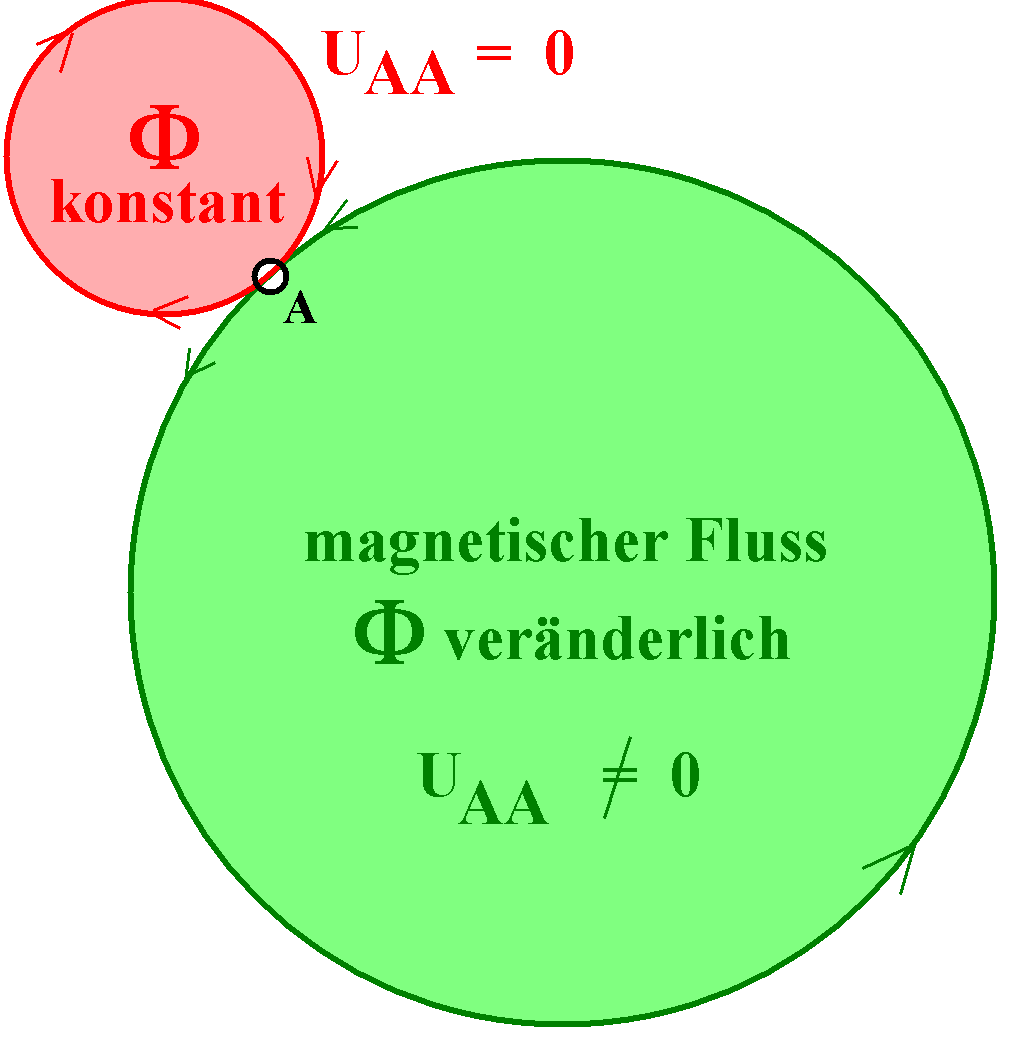 |
Du hättest das Induktionsgesetz auch so formulieren
können:
Gemessen werden soll die Spannung UAA von einem
Punkt A zum Punkt A (!). Vielleicht kommt dir die Frage
eigenartig vor. Aber:
Wenn der Weg von A nach A einen sich zeitlich ändernden
magnetischen Fluss Φ einschließt (grün), ist diese Spannung in
der Regel von 0 verschieden und heißt Induktionsspannung. Sie
ist eine Ringspannung.
Wenn der Weg von A nach A einen konstanten oder gar keinen
magnetischen Fluss Φ einschließt (rot), gibt gibt es keine
Induktion, ist die Induktionsspannung 0.
|
.
Damit hängt eine überraschende Folgerung zusammen: Die Induktionsspannung
"längs der geschlossenen Linie" von A nach A hängt von der Änderung des
gesamten eingeschlossenen magnetischen Flusses ab. Das gilt offenbar
sogar dann, wenn an den Orten der geschlossenen Linie überhaupt kein
Magnetfeld herrscht! Ein Anzeichen für die so genannte "Nichtlokalität
der Induktion". Im Internet findet man viele überflüssige
Diskussionen von Leuten, denen das nicht bewusst ist.
Mit einem Experiment kann das einigermaßen schlüssig gezeigt werden: In
einer Feldspule steckt ein Eisenkern, über den eine Induktionsspule
gesteckt ist, deren Windungen relativ nahe am Kern verlaufen. Man kann
davon ausgehen, dass quasi der gesamte magnetische Fluss auf das Innere
des Kerns beschränkt ist, dass außerhalb von ihm das Magnetfeld quasi 0
ist. Dennoch erhält man eine Induktionsspannung, wenn man z.B. einen
dreiecksförmig sich verändernden Strom durch die Feldspule schickt. Im
Inneren des Kerns und damit der Induktionsspule ändert sich der Fluss,
also Induktion.
(Aus dem einen Ende des Kerns tritt das magnetische Feld
aus, es muss beim anderen Ende wieder eintreten; alle magnetischen
Feldlinien müssen beim B-Feld ja geschlossen sein. Der
magnetische Fluss muss also außerhalb des Kerns wieder "zurückkehren".
Also kann das Magnetfeld außerhalb des Kerns nicht exakt 0 sein. Im
Vergleich zum gesamten Raum außerhalb des Kerns entfällt davon aber auf
die Windungsfläche der Induktionsspule ein vernachlässigbarer
Flussanteil und trägt so quasi nicht zur Induktion bei.)
Und noch eine Folgerung ergibt sich aus dem Induktionsgesetz: Der
magnetische Fluss, der von einer geschlossenen Leiterschleife
eingeschlossen wird, kann sich offenbar auch dadurch ändern, dass zwar das
Magnetfeld B zeitlich konstant ist, aber sich die Orientierung der
Windungsfläche im Vergleich zur Magnetfeldrichtung ändert. Das kann auch
so beschrieben werden, dass sich die vom Magnetfeld senkrecht durchsetzte
Fläche A ändert. Wir kennen das von Versuch 7 in Abschnitt 3. Das ist z.B.
auch der Fall, wenn eine Induktionsspule im konstanten (homogenen oder
nichthomogenen) Magnetfeld gedreht wird. Ein Versuch zeigt das:
 |
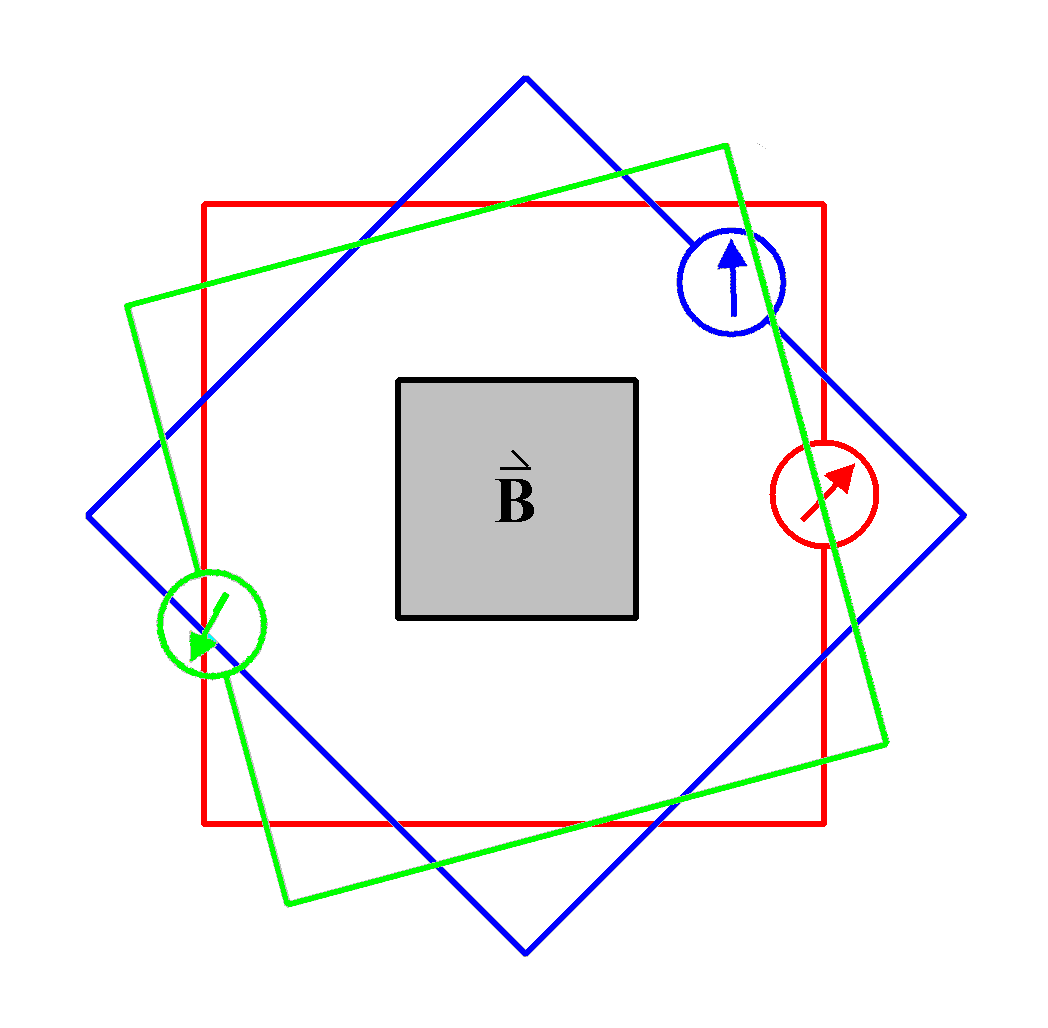
Versuch: Eine Induktionsspule dreht sich im zeitlich
konstanten Magnetfeld zwischen den Spulen eines
Helmholtzspulenpaars, angestoßen mit der Hand. Das trägheitslose
Zeigerinstrument zeigt eine oszillierende Induktionsspannung an,
deren Maximalwert immer geringer wird, je langsamer sich die Spule
dreht.
Von der Induktionsspule aus gesehen tritt das Magnetfeld einmal
auf der roten Seite der Induktionsspule ein, dann wieder auf der
blauen Seite. Der magnetische Fluss in der Induktionsspule ändert
sich, also Induktion. Aber auch die Größe der dem Magnetfeld
senkrecht dargebotenen Windungsfläche ändert sich.
|
 |
.
Rechnerisch sieht das so aus: ΔΦ = Δ (B · A) = ΔB · A + B · ΔA = B · ΔA
(bis auf das letzte Gleichheitszeichen gelten alle Gleichheitszeichen
immer, wenn sich ein Fluss dreiecksförmig ändert. Eine Änderung des
magnetischen Flusses kann es selbst bei konstantem Magnetfeld geben, wenn
sich die Windungsfläche ( ΔA) ändert ***).
Wenn du schon die Ableitung kennst, kennst du auch die
Produktregel für die Ableitung nach der Zeit, die besagt: Φ·
= (B · A )· = B· · A + B ·
A· .
.
.
8. Das Induktionsgesetz in verschiedenen
Situationen
1. linear veränderlicher magnetischer Fluss
2. Bewegung der Induktionsschleife durch ein konstantes magnetisches Feld
hindurch
3. Drehung einer Induktionsschleife mit konstanter
Winkelgeschwindigkeit in einem konstanten magnetischen Feld
4. sinusförmig veränderlicher magnetischer Fluss und ruhende
Induktionsschleife
5. unterschiedliche Spannungen zwischen zwei Punkten einer
Induktionsschleife - auch hier bewährt sich der Begriff der Ringspannung
Vgl. PDF-Datei
.
.
9. Kann man Induktion verstehen?
"Verstehen" heißt in der Physik: eine neue Erkenntnis auf einen bereits
bekannten und wohl vertrauten Sachverhalt zurückführen. Im Allgemeinen
kann man die Induktionsspannung nicht auf frühere Kenntnisse zurückführen.
Induktion ist eine völlig neue Erscheinung, die man gesetzmäßig erfassen
kann, aber nicht in dem Sinn "verstehen" kann, dass man sie auf frühere
Kenntnisse zurückführt. Man kann nur die Bedingung und deren Folge nennen:
"Wenn sich in einer geschlossenen Kurve C der magnetische Fluss ändert,
entsteht längs dieser Kurve eine Ringspannung." Deswegen haben Michael
Faraday (um 1831) und ca. 40 Jahre später James Clark Maxwell das
Induktionsgesetz wie oben als eines der vier "Grundgesetze" der
Elektrizitätslehre ("Elektrodynamik") formuliert, das sich nicht auf
andere zurückführen lässt.
Es gibt einen Ausnahmefall, der sich sehr wohl auch auf frühere
Kenntnisse zurückführen lässt:
.
.
10. Zusammenhang mit der Lorentz-Kraft in
Sonderfällen
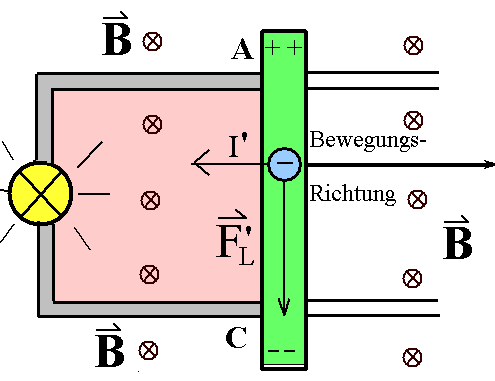 |
Auf einem U-förmigen Leiterbügel gleitet eine Leiterbrücke in
einem zeitlich konstanten Magnetfeld. Im Inneren der so gebildeten
Leiterschleife entsteht also ein zeitlich veränderlicher
magnetischer Fluss. Der U-förmige Leiterbügel ruht in einem
Bezugssystem mit einem Magnetfeld B. In ihm bewegt sich -
senkrecht zu den Magnetfeldlinien - der Leiterbügel mit der
Geschwindigkeit v (In Bewegungsrichtung). Auf die mit
dieser Bewegung "mitgerissenen" Leitungselektronen in der
Leiterbrücke entsteht eine Lorentz-Kraft, die die Elektronen zu
einem Ende der Leiterbrücke hin drängt. Über den U-förmigen
Leiterbügel fließen die Elektronen wieder zum anderen Ende der
Leiterbrücke zurück. Dabei wird eventuell Energie am
Leitungswiderstand des Leiterbügels in innere Energie, Licht und
Wärme umgesetzt.
Woher kommt diese Energie? Sie kann nur aus der Arbeit kommen,
die durch die Lorentz-Kraft FL'
verrichtet wird (bzw. die letzten Endes durch mechanische Arbeit
zur Bewegung der Leiterbrücke von außen zugeführt wird). Also
gilt für die Arbeit für einen vollen Umlauf:
WO = WLorentz, AC + WCA
(Die Arbeit für die Verschiebung von C nach
A über das Lämpchen, WCA = 0 , weil im
Außenraum zwischen C und A keine Kraft wirkt, welche Energie
zuführt, die also den Ringstrom antreiben könnte).
Also entsteht auch hier eine Ringspannung, zu der es aber nur
vom Bereich des Leiterbügels her einen Beitrag gibt: durch die
Lorentz-Kraft. Wie oben gilt beim Transport der Ladung q:
WLorentz, AC = q·B·v·ℓ bzw. für die
Ringspannung UO = B·ℓ·v. *)
Mit Hilfe der Lorentz-Kraft bekommst du also in diesem Fall
die richtige Induktionsspannung (Ringspannung) heraus.
(rosa in den beiden Zeichnungen: von der geschlossenen
Kurve umfasster magnetischer Fluss. Er ändert sich mit der
eingeschlossenen Fläche, wenn die grüne Leiterbrücke
verschoben wird.)
|
Du kannst jetzt auch klären, weshalb die Proportionalitätskonstante
im Induktionsgesetz gerade den Betrag 1 hat:
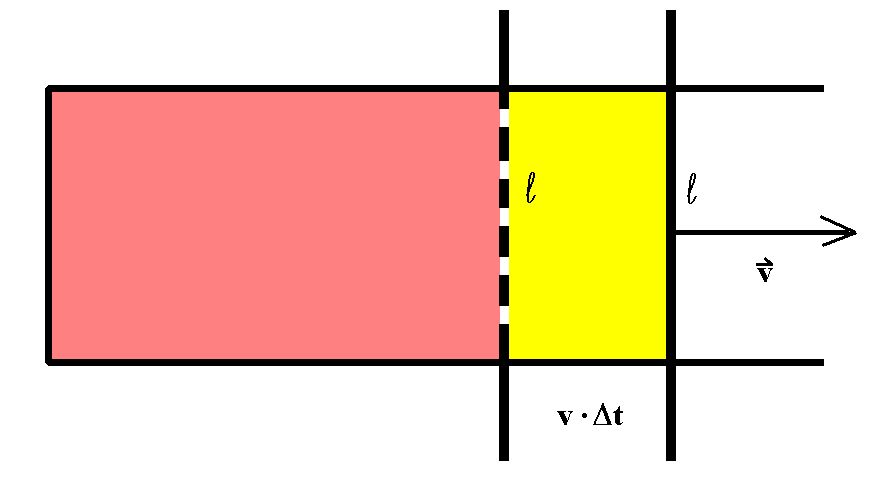 |
Ergänzt man nämlich die Leiterbrücke (den Stab) von
Abschnitt 10 durch einen U-förmigen Leiter, der im Labor ruht,
gegenüber dem sich also die Leiterbrücke mit der Geschwindigkeit
v bewegt, dann wird die eingeschlossene Fläche A im
Zeitintervall Δt um ℓ·v·
Δt verändert (um den gelb gezeichneten Anteil).
Dementsprechend ändert sich der magnetische Fluss um Δ
Φ = B·ℓ·v·Δt, also
Δ Φ/ Δt = B·ℓ·v.
Weil hier die Windungszahl n = 1 ist, entspricht das bis
auf das negative Vorzeichen direkt der Induktionsspannung
UO = B·ℓ·v,
deren Betrag in Abschnitt 10 mit der Lorentz-Kraft
hergeleitet wurde. Die Übereinstimmung zeigt: Ein eventueller
Faktor, die Proportionalitätskonstante im allgemeinen
Induktionsgesetz, muss den Betrag 1 haben!
|
.
.
11. Jetzt hast du also zwei Möglichkeiten zur Verfügung
um eine Induktionsspannung zu berechnen:
a) mit Hilfe des allgemeinen Induktionsgesetzes: UO = -
n · Φ· Das funktioniert immer. Du musst
allerdings angeben können, mit welcher Geschwindigkeit sich der
magnetische Fluss ändert, also Φ· . Im Fall einer
linearen zeitlichen Änderung des magnetischen Flusses gilt: Φ·
= ΔΦ/Δt.
b) mit Hilfe der Lorentz-Kraft: FL = q·v·B . Das
funktioniert aber nicht immer.Es gibt keine Lorentz-Kraft, wenn keine
Bewegung im Vergleich (relativ) zu dem Bezugssystem stattfindet, in dem
das Magnetfeld gemessen wird.
Wenn beide Verfahren funktionieren, kommt natürlich beidemale das
gleiche heraus.
Es gibt keinen Widerspruch zwischen den beiden Betrachtungen a) und b).
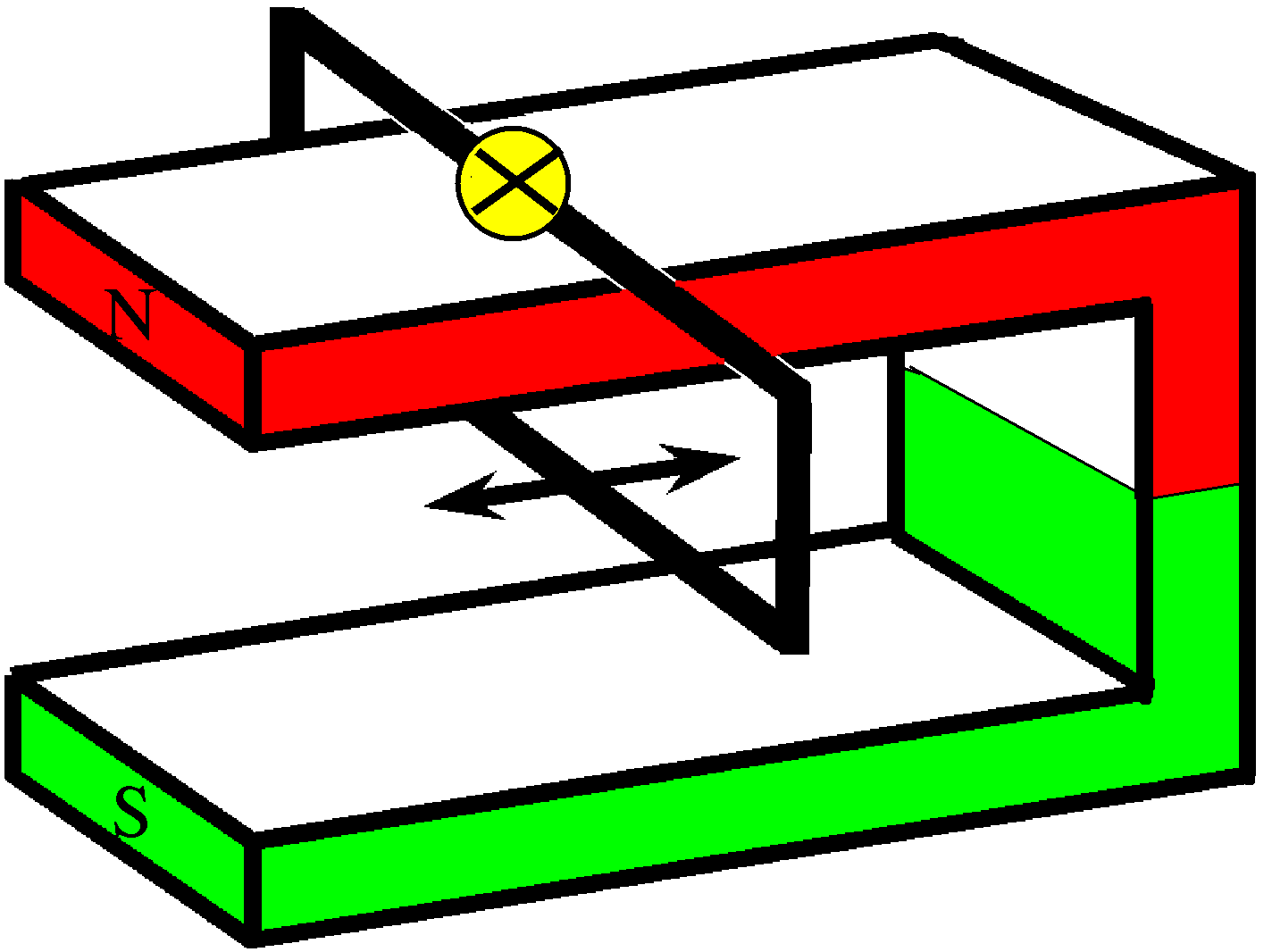 |
Beispiel:
Betrachte einen Hufeisenmagneten, über dessen einen Schenkel ein
rechteckiger gut leitender Ring gesteckt wird. Diesmal soll der Ring
hin und her bewegt werden, längs des Schenkels in
Pfeilrichtung.
Auch in diesem Fall eines leitenden Rings, der auf einem Schenkel
eines Hufeisenmagneten hin und her bewegt wird führen beide
Betrachtungsweisen: a) mit der Flussänderung durch das Magnetfeld
im Schenkel bzw. b) mit der Lorentz-Kraft zwischen den
Schenkeln im Sinne des Induktionsgesetzes zur gleichen
Induktionsspannung.
Im Realversuch ersetzt man das Lämpchen wieder
durch einen empfindlichen Spannungsmesser.
|
Merkwürdig ist das aber schon: Einmal wurde die Lorentz-Kraft allein auf
die Ringseite im homogenen Feld herangezogen (zwischen den
Schenkeln des Magneten), das andere Mal das "weit" entfernte magnetische
Feld in dem Schenkel. Das ist ein Anzeichen für die "Nichtlokalität
der Induktion": Ursache für sie sind nicht Vorgänge an einer bestimmten
Stelle (nichtlokal = nicht an einem bestimmten Ort). Grund ist, wie man
zeigen kann, dass die Felder an der Stelle der Lorentz-Kraft mit den
Feldern im Inneren des Schenkels eng zusammenhängen. Das ist eine Folge
der Tatsache, dass das Magnetfeld B nur geschlossene Feldlinien
hat.
.
.
12. Was geschieht, wenn kein geschlossener Stromkreis
vorliegt?
Ein Leiter oder eine Spule mit offenen Enden lässt sich leicht zu
einer geschlossenen Kurve C erweitern, die den sich ändernden magnetischen
Fluss umgibt. Das kann mit dem (hochohmigen) Spannungsmesser und seinen
leitenden Zuführungen geschehen, oder einfach mit einer gedachten Kurve.
Für diese geschlossene Kurve C gilt wieder das Induktionsgesetz. Zu einem
Ringstrom kann es ohne leitende Verbindung offenbar nicht kommen,
wohl aber zu einer Ringspannung.
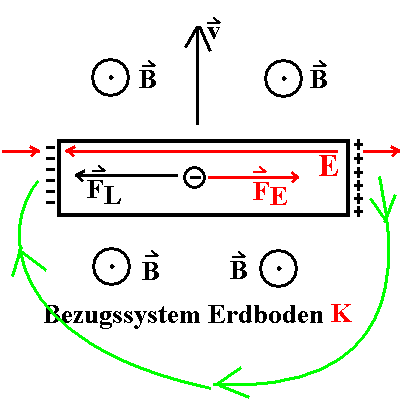
Die Folge der Ringspannung erkennst du am einfachsten an
einer Leiterbrücke (Metall-Stab), die im Magnetfeld gleitet, und
zwar so, dass die Leiterbrücke bei ihrer Bewegung "Magnetfeldlinien
senkrecht schneidet". Die restlichen Teile der Kurve C sollen in dem
Bezugssystem K ruhen, in dem das Magnetfeld B gemessen wird.
 |
Um die Ringspannung zu berechnen müssen wir die Arbeit für den
Transport einer Ladung längs eines vollen Umlaufes untersuchen. Hier
spielt die Lorentz-Kraft die entscheidende Rolle.
1. Fall: Geschlossener Stromkreis aus Leitern:
Auf der oben beschriebenen geschlossenen Kurve C erhalten wir
aber nur einen einzigen Beitrag als Folge der Lorentz-Kraft FL
im Stab: Leitungselektronen werden an das eine Ende der
Leiterbrücke verschoben. Die Lorentz-Kraft ist bei homogenem B-Feld
und konstanter Geschwindigkeit v konstant und in der
ganzen Leiterbrücke gleich. Deshalb verrichtet die konstante
Lorentz-Kraft eine Arbeit an einem Elektron der Ladung q
gemäß W = FL· ℓ . Es gilt dann also W = q·B·v·ℓ,
wenn ℓ die Länge der Leiterbrücke ist.
Das ist der einzige Beitrag zur Arbeit für einen vollen Umlauf,
weil es außerhalb des Stabs keine Lorentz-Kraft gibt.
Also gilt für die Ringspannung UO = W/q = B·ℓ·v.
2. Fall: Wenn aber der Stab elektrisch isoliert
ist, "stauen" sich die Leitungselektronen an dem einen Ende des
Stabs. Es entsteht ein Minuspol und am anderen Ende der
Leiterbrücke ein Elektronenmangel bzw. ein Pluspol. Das ist also
hier die Folge der Ringspannung.
|
Während sich im isolierten Stab der Minus- und der Pluspol
allmählich ausbilden, geschieht etwas Neues: Durch die verschobenen
Ladungen entsteht zusätzlich ein elektrisches Feld E vom Pluspol
zum Minuspol. Sein Aufbau ist beendet, wenn Kräftegleichgewicht zwischen
der Lorentz-Kraft und der sekundären elektrischen Kraft FE
= q·E entstanden ist. Da die Lorentz-Kraft bei homogenem B-Feld
und konstanter Geschwindigkeit v konstant und in der ganzen
Leiterbrücke gleich ist, ist das sekundäre elektrische Feld E ein
homogenes Feld, wie in einem idealen Plattenkondensator, und das
unabhängig von der Form der Leiterbrücke! Wie im Plattenkondensator ist
mit diesem sekundären elektrischen Feld eine Potenzialdifferenz verbunden:
Das positive Ende der Leiterbrücke liegt auf höherem Potenzial als das
negative Ende. Da das Feld homogen ist, gilt wie im Plattenkondensator für
diese Potenzialdifferenz U = E·ℓ = B·ℓ·v . Sie ist von gleichem Betrag wie
die Ringspannung.
Was wurde also gemacht? Mit einem Trick - dadurch, dass der
Stromkreis jetzt nicht geschlossen ist - erzeugten wir zusätzlich zur
Ringspannung eine gewöhnliche Spannung (Potenzialdifferenz) von
gleichem Betrag. Durch sie können wir die Ringspannung messen, auch dann,
wenn kein Ringstrom entstehen kann. Ist aber der Stromkreis geschlossen,
also bei vorhandenem Ringstrom, gibt es diese sekundäre gewöhnliche
Spannung nicht mehr (es "stauen" sich keine Ladungen mehr). Da sie von
gleichem Betrag wie die Ringspannung ist, bestimmt ihr Betrag aber immer
noch die Größe des Ringstroms für den Fall, dass dieser möglich ist und
die gewöhnliche Spannung nicht existiert.
Wie würde das sekundäre Feld E - für sich genommen - auf ein
Elektron wirken? Im Inneren der Leiterbrücke würde es das Elektron vom
Minus- zum Pluspol treiben (wenn nicht die Lorentz-Kraft wirken würde),
außerhalb der Leiterbrücke aber ebenfalls vom Minus- zum Pluspol. Es kann
nicht für einen Ringstrom sorgen; es hat im Inneren der Leiterbrücke die
"falsche" Richtung, abgesehen davon, dass es bei einem geschlossenen
Stromkreis gar nicht existiert. Dagegen sorgt die Ringspannung eindeutig
dafür, dass Leitungselektronen im geschlossenen Stromkreis immer im
Kreis herum fließen: Außerhalb der Leiterbrücke vom Minus- zum Pluspol und
innerhalb der Leiterbrücke weiter vom Plus- zum Minuspol und so fort,
immer im Kreis herum.
| Das sekundäre elektrische Feld erzeugt eine gewöhnliche
elektrische Spannung (Potenzialdifferenz), wenn der Stromkreis nicht
geschlossen ist. Diese ist zwar von gleichem Betrag wie die
Ringspannung UO, ist aber nicht in der Lage, den
beobachteten Ringstrom zu erklären. |
Zur Erklärung der Hall-Spannung in einem ähnlichen Fall ist die
Herleitung aber korrekt.
Wegen der betragsmäßigen Übereinstimmung nennen viele Schulbücher die
sekundär entstandene gewöhnliche Spannung "Induktionsspannung". Dass sie
diese Situation meinen, erkennst du an der typischen Formulierung "zwischen
den Enden einer Spule, eines im Magnetfeld bewegten leitenden
Stabs oder einer Leiterschleife entsteht eine Induktionsspannung".
Da durch das Aufbrechen des Stromkreises (getrennte Enden!) und dem Einbau
des hochohmigen Spannungsmesser ein Strom verhindert wird, entsteht die
Situation dieses Abschnitts: kein geschlossener Stromkreis.
| Wir verstehen mit der Ringspannung darüber hinaus sogar, dass
das auch dann der richtige Betrag der Induktionsspannung ist,
wenn ein Induktionsstrom fließt. |
Beachte auch: Man muss sehr vorsichtig sein, wenn man mit Feldlinien
argumentiert. Im Kapitel über das Magnetfeld
hast du ja erfahren, dass Feldlinien nur gedachte Linien sind, ein
Modell, das manchmal recht nützlich ist, aber auch manchmal in die
Irre führt.
.
13. Woher kommt die Energie?
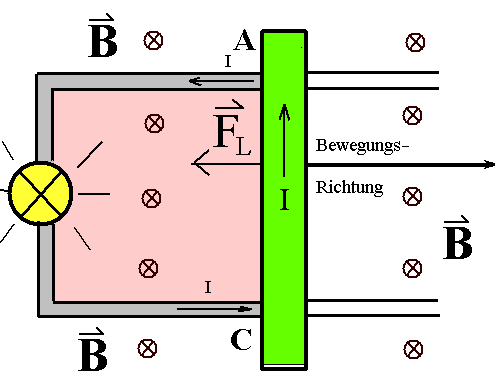 |
Die Situation ist wie oben: Als Folge der Lorentz-Kraft FL'
im obigen Bild werden Elektronen an das untere Ende der
Leiterbrücke gedrängt und fließen über den äußeren Stromkreis
wieder an das obere Ende zurück. Das ist mit einem Strom I
verbunden, der gemäß der Zeichnung links orientiert ist. Auf einen
Strom senkrecht zum Magnetfeld B entsteht wieder eine
magnetische Kraft FL , die der Bewegung
entgegengerichtet ist. (Da jetzt von einem anderen Strom, I, die
Rede ist, handelt es sich auch um eine andere Lorentz-Kraft als
oben.)
Zur Richtungsentscheidung dient eine Hand-Regel, z.B. die
Rechte-Hand-Regel, bei der der Daumen in Stromrichtung (I) zeigt
**). Diese magnetische Kraft FL
würde den Leiterbügel schnell stoppen, wenn man keine
Gegenmaßnahme ergreifen würde: eine Kraft von außen, die in
Bewegungsrichtung, entgegengesetzt zu FL,
wirkt. Mit ihrer Hilfe wird bei der Bewegung der Leiterbrücke
mechanische Arbeit verrichtet.
Der Induktionsstrom I ist also so gerichtet, dass eine Kraft FL
entsteht, gegen die von außen eine mechanische Arbeit verrichtet
werden muss, damit sich die Leiterbrücke in Bewegungsrichtung
mit konstanter Geschwindigkeit bewegen kann. Das ist hier die
Aussage der Regel von Lenz.
Die Energie, die das Lämpchen auf dem Umweg über die Induktion
zum Leuchten bringt, wurde also von demjenigen aufgebracht, der
die Leiterbrücke in Bewegungsrichtung "mit Gewalt" gezogen hat.
Mit Hilfe der Induktion wurde also mechanische Arbeit in
elektromagnetische Energie (im elektrischen und magnetischen
Feld innerhalb der Windungsfläche und ihrer Umgebung) und dann
weiter in innere Energie, Licht und Wärme umgewandelt.
Würdest du das Lämpchen aus der Fassung schrauben, könnte kein
Strom I fließen, es würde keine Energie nach außen abgestrahlt
werden, und es müsste niemand Arbeit verrichten, um die
Leiterbrücke in Bewegungsrichtung zu verschieben. Ohne Reibung
würde sie sich - einmal angestoßen - immer mit konstanter
Geschwindigkeit weiter bewegen.
|
.
.
14. Ringspannung und Stromstärke
Auch für die Ringspannung gilt bei einem geschlossenen Stromkreis mit
dem Gesamtwiderstand R das Ohm'sche Gesetz:
Nehmen wir einmal an, es wird in einer Zeit Δt eine Ladungsmenge Q in
einem vollen Umlauf durch den Kreis transportiert. Dann ist dazu die
Arbeit W = UO.Q aufzuwenden. Weil aber Q = I.Δt
haben wir also
| UO·I
· Δt = R·I2
· Δt (*). |
Du kennst vielleicht die Gesetzmäßigkeit für die Leistung P (= Arbeit
pro Zeiteinheit), die bei einem Strom I an einem Widerstand R in innere
Energie und Wärme umgesetzt wird:
Damit kannst du die Gleichung (*) deuten: Das ist eine Aussage des
Energiesatzes! Links steht die Energie, die bei einem vollen Umlauf der
Ladung Q durch die Induktion zugeführt wird, rechts die Energie, die in
der gleichen Zeit Δt im Widerstand R des Stromkreises als Wärme nach außen
abgegeben wird. Das musste man erwarten können: Nämlich, dass die in einer
Zeit Δt nach außen abgegebene Energie nur von der in der gleichen Zeit
durch die Induktion zugeführten Energie herkommen kann. Weil dies so
vernünftig heraus kommt, können wir dem Ohm'schen Gesetz in der oben
aufgeführten Form vertrauen. Es bestätigt die anfänglichen Versuche, nach
denen der sich ausbildende Strom von der Ringspannung, aber auch vom
Widerstand R abhängt. So lässt sich die jeweilige Stromstärke berechnen.
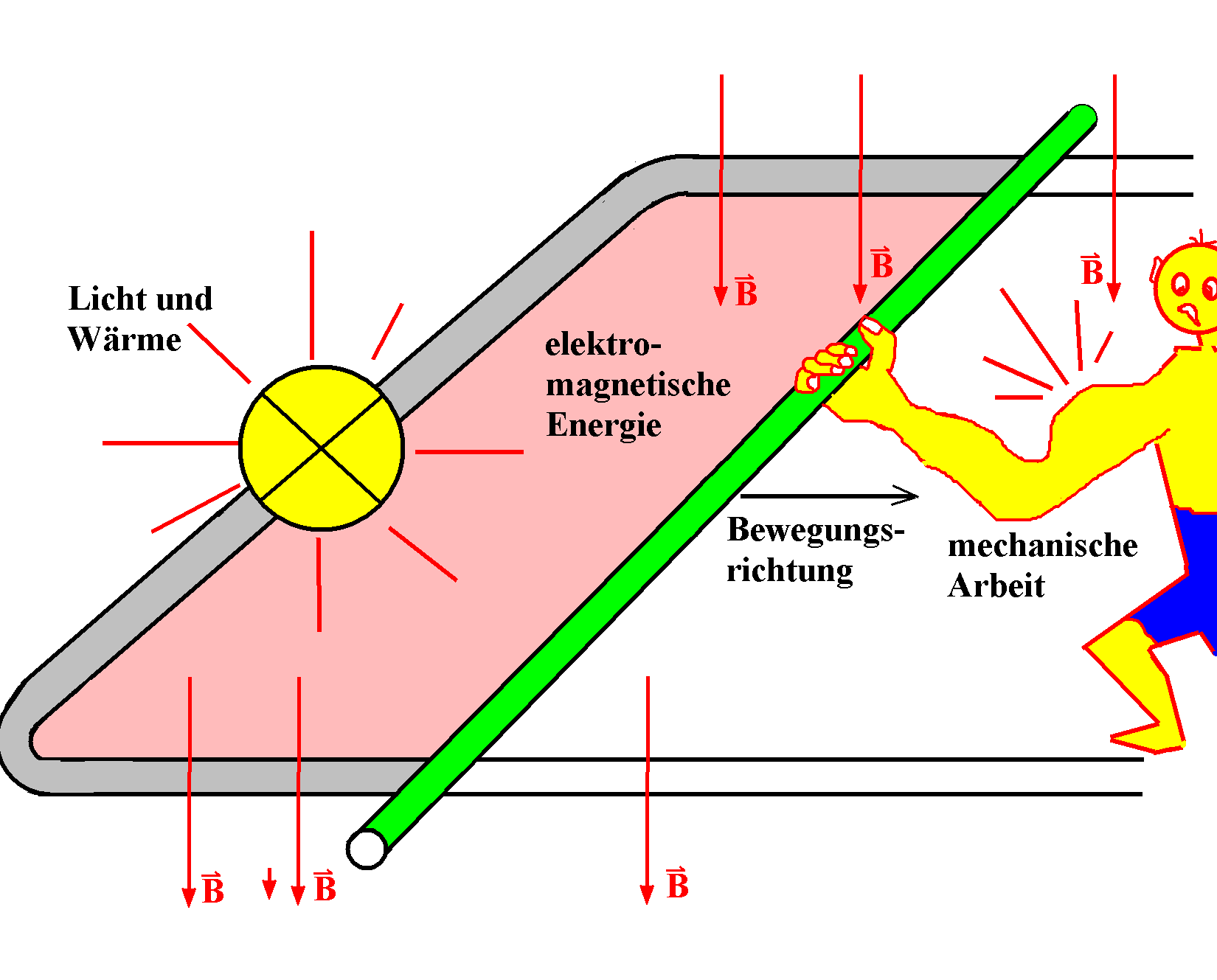 |
Die grüne Leiterbrücke wird im Magnetfeld mit "Gewalt" über
einen U-förmigen Leiterbügel gezogen, bei gutem Kontakt mit dem
U-Leiter.
Bei diesem einfachsten Typ eines Generators wird mechanische
Arbeit mittels der Induktion in elektromagnetische Energie
umgewandelt, die schließlich durch ein Lämpchen als Licht und
Wärme abgestrahlt wird.
Diese Erscheinung, dass in Generatoren durch Induktion
mechanische Arbeit in elektromagnetische Energie umgewandelt
wird, ist einer der Gründe für die überragende Bedeutung der
Induktion.
(rosa in der Zeichnung: von der geschlossenen Kurve
umfasster magnetischer Fluss. Er ändert sich mit der
eingeschlossenen Fläche, wenn die grüne Leiterbrücke
verschoben wird.)
|
.
.
15. Eine Aufgabe erläutert den Begriff der
Ringspannung im Unterschied zur gewöhnlichen Spannung
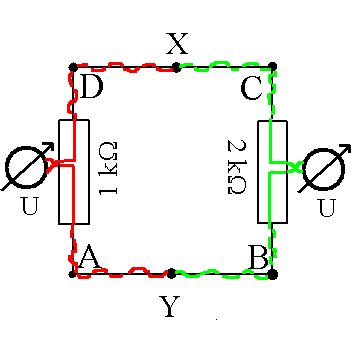 |
Aufgabe:
In der nebenstehenden Schaltung sollen zwei Spannungen zwischen
denselben Punkten X und Y gemessen werden, und zwar mittels der
roten und der grünen Anschlussleitungen. Ist das nicht
eine ziemlich sinnlose Frage? Muss dabei denn nicht die
gleiche Spannung herauskommen?
Zwei Widerstände bilden zusammen mit geraden Leiterstücken ein
Quadrat. Die Anschlussleitungen sind um die Quadratseiten
gewickelt bzw. miteinander verdrillt, so dass kein zusätzlicher
magnetischer Fluss eine Rolle spielt. Die
Änderungsgeschwindigkeit des magnetischen Flusses ΔΦ/Δt
im Quadrat soll gerade - 6 V sein.
a) Gib die Ringspannung an!
b) Berechne die Stromstärke ("Spannung macht Strom")!
c) Berechne Urot und Ugrün als
Spannungsabfälle an den Widerständen bei Stromfluss ("Strom
macht Spannung")!
d) Wie lässt sich das überraschende Ergebnis Ugrün
≠ Urot (sogar Ugrün = 2·Urot )
trotz Messung zwischen den gleichen Punkten X und Y erklären?
|
|
|
.
16. Warnungen
1. Nach der Herleitung der Ringspannung über die Lorentz-Kraft
könnte man meinen, dass die Induktionsspannung dort lokal erzeugt wird,
wo die Lorentz-Kraft entsteht, also im Leiter. Andererseits ändert sich
der von der Windung eingeschlossene magnetische Fluss in der gesamten
Windungsschleife. Deswegen ist es im Allgemeinen nicht sinnvoll, die
Induktion als einen lokalen Effekt zu betrachten, der an einem
bestimmten Ort stattfindet. Eine solche Betrachtungsweise hat schon zu
vielen Missverständnissen geführt, die in der Literatur heftig
diskutiert wurden, auch von esoterischen Kreisen. Vielmehr sollte man
den gesamten von der Windung eingeschlossenen magnetischen Fluss
im Auge haben, der sich ändert, und die Ringspannung längs der gesamten
Windung. Nur über deren Zusammenhang macht das Induktionsgesetz eine
allgemeine Aussage. ("Nichtlokalität der
Induktion")
2. In Schulbüchern wird manchmal zwischen einer "Induktion im
bewegten Leiter" und einer "Induktion im ruhenden Leiter"
unterschieden. Solche Bezeichnungen sind aus zwei Gründen sinnlos
und irreführend. Denn jeder beliebige Leiter ist bewegt und
zugleich ruht jeder beliebige Leiter. Das ist nur eine Frage des
Bezugssystems, von dem aus der Leiter betrachtet wird. Für das
allgemeine Induktionsgesetz, formuliert mit dem sich zeitlich ändernden
magnetischen Fluss, ist eine Unterscheidung zwischen verschiedenen Arten
der Induktion überflüssig. Zudem findet, wie eine genauere
Betrachtung und Experimente zeigen, Induktion überhaupt nicht
speziell
in einem Leiter statt. Es handelt sich
vielmehr um einen Zusammenhang zwischen zeitlichen Änderungen des
Magnetfelds und einem entstehenden elektrischen Feld im ganzen Bereich
in und um der Windungsfläche. Das Missverständnis, dass die Induktion in
einem Leiter stattfinde, hat zu vielen kuriosen Diskussionen
geführt, von denen man einige Kostproben im Internet nachlesen kann. Was
mit einer "Induktion im ruhenden Leiter" bezeichnet wird, sollte eher
heißen "Induktion bei einer zeitlichen Änderung des Magnetfelds B"
im Unterschied zu einer Situation, bei der der eingeschlossene
magnetische Fluss durch eine Flächenänderung der Windungsschleife
variiert.
.
| Hinweis: Bei
all diesen Ausführungen setzten wir uns sozusagen in die
Leiterschleife hinein und betrachteten alles Geschehen von dort
aus. Andere Autoren bevorzugen dagegen das Laborsystem, in dem das
Magnetfeld ruht. Das ist durchaus möglich und führt zu denselben
quantitativen Ergebnissen. Viele der Beschreibungen und
Interpretationen müssen aber geändert werden. Man muss dann auch
zwischen unterschiedlichen "Arten von Induktion" unterscheiden,
wobei nicht immer ein elektrisches Wirbelfeld entsteht. Eine
solche Sichtweise scheint mir komplizierter zu sein als die hier
vorgestellte. |
.
*) Dass die
Erklärung mit der Lorentz-Kraft funktioniert, hängt damit zusammen, dass
nach Einsteins Relativitätstheorie in gewisser Weise Lorentz-Kraft und
Induktion zwei Seiten derselben Medaille sind. Das soll hier aber nicht
erklärt werden. Mit der Lorentz-Kraft hast du also in diesem Sinn schon
früher einen Aspekt der Induktion kennen gelernt.
**) Die Stromrichtung
(I) ist hier immer die so genannte "technische Stromrichtung",
entgegengesetzt zu einer eventuellen Bewegungsrichtung von Elektronen
***) Es gilt ΔΦ = Δ (B ·
A) = B(t + Δt) · A(t + Δt) - B(t) · A(t)
= B(t + Δt) · A(t + Δt) - B(t + Δt) · A(t) + B(t + Δt) ·
A(t) - B(t) · A(t)
= B(t + Δt) · [ A(t + Δt) - A(t) ] + [ B(t + Δt) - B(t )
] · A(t)
= B(t + Δt) · ΔA + ΔB · A(t)
Berücksichtigst du, dass für sehr kleine Δt gilt: B(t +
Δt) ≈ B(t) , erhältst du ΔΦ = B(t) · ΔA + ΔB · A(t)
( zurück )
(zuletzt aktualisiert April 2013)























