Startseite FORPHYS Physik für Schülerinnen und Schüler Didaktogene Lernschwierigkeiten im Physik-UR Anschauliche Mechanik   Elektrischer Stromkreis   Schüler- versuche Physik Lernen mit dem Computer  Meta- Physika- lisches  Begriff- liches Experi- ment des Monats Im- pres- sum Kommentare und Wünsche © Horst Hübel Würzburg 2005 - 2014

Hat Spannungsabfall bei einem stationären Strom etwas mit "gestauten Elektronen" zu tun?

nach W. Panofsky, M. Phillips, Classical electricity and magnetism, Addison-Wesley Publishing Company, 2. Auflage 1962  und vielen anderen Standard-Lehrbüchern der Elektrodynamik

1. Wird in einem geschlossenen Stromkreis ein Widerstand von einem Strom durchflossen, entsteht an ihm ein Spannungsabfall. Manchmal wird als Modell für Spannungsabfälle an hintereinander geschalteten Widerständen ein "Elektronenstau" vorgestellt: Weil sich vor jedem Widerstand "Elektronen stauen", herrsche nach dieser Meinung dort gegenüber dem anderen Pol des Widerstands eine Potenzialdifferenz. Damit hängt das von mir so genannte "Elektronenstaumodell des elektrischen Stromkreises" zusammen. Wie weit ist es gerechtfertigt?

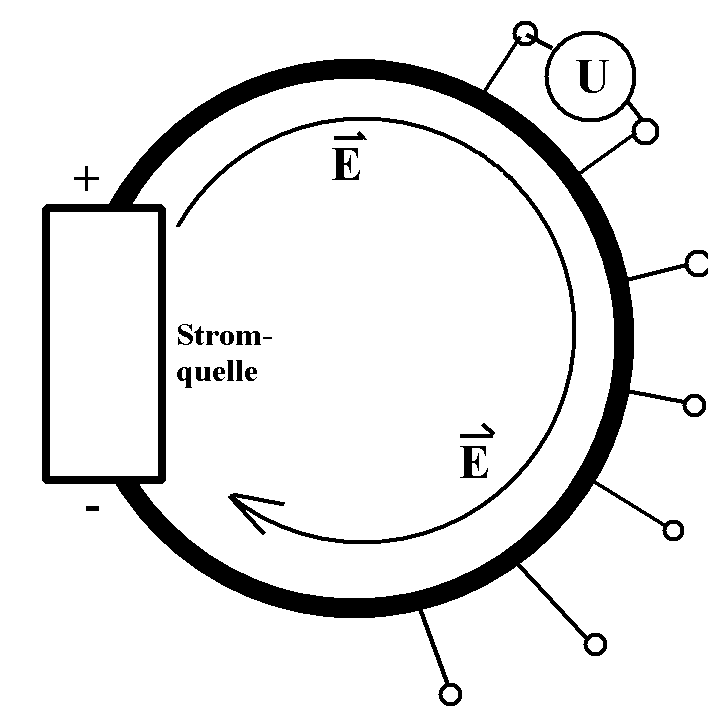
Die Widerstände sollen zunächst aus einem einzigen sehr langen, dünnen, homogenen Leiter (mit der konstanten spezifischen Leitfähigkeit σ) bestehen mit mehreren Abgriffen. Wegen des Ohm'schen Gesetzes 

                                                                       j = σ·E  

Abb. 1: Stromkreis mit vielen Abgriffen zur Spannungsmessung

muss in ihm bei konstanter Stromdichte j auch konstante elektrische Feldstärke E herrschen.

Das empirische ohmsche Gesetz bedingt, dass sich j und E zueinander passend einstellen müssen. Andererseits gilt:  

                                                                       div E = ρ/ε₀.

Danach sind Ladungen mit der Ladungsdichte ρ Quellen und Senken des elektrischen Feldes.

Da E im Inneren eines homogenen Leiters (Widerstands) wirbelfrei und homogen ist ( rot E = 0 und div E = 0 , aus Symmetriegründen), muss dort ρ = 0 sein. Es können dort nirgends gestaute Elektronen auftreten! Dennoch gibt es einen Spannungsabfall an dem Widerstand oder zwischen Teilen des Widerstands. Damit ist noch nicht ausgeschlossen, dass an den Klemmen der Stromquelle oder Übergangsstellen zwischen unterschiedlichen Leitern andere Verhältnisse vorliegen.

2.  Stromkreis mit variabler Leitfähigkeit σ

Wenn nun aber  sich die Leitfähigkeit σ beim Übergang von einem Widerstand zum anderen ändert? Dann gilt:   

(*)       div j  =  div  ( σ · E )  =   σ · div E  + E · (grad  σ )   =  0 , also

   σ · (ρ/ε₀)   = - E · ( grad  σ )           bzw.       ρ   = - E · ( grad  σ )   ·  ε₀/σ                    

In diesem Fall kann ρ tatsächlich an der Übergangsstelle von 0 verschieden sein, wenn grad σ ≠ 0. Die Ladungsanhäufungen *) sorgen jetzt dafür, dass sich die für das ohmsche Gesetz erforderliche richtige elektrische Feldstärke im Leiter ausbilden kann. Sie sorgen offenbar für eine Anpassung der elektrischen Feldstärke, nicht für ihre Existenz, denn beim früheren Beispiel gab es ja E ohne Ladungsanhäufung! Besonders auffällig sind solche Ladungsverteilungen und elektrischen Feldstärken in der Nähe eines p-n-Übergangs bei Halbleitern. Solche Ladungsverteilungen gibt es offenbar auch an den Anschlüssen getrennter Widerstände, also dort, wo sich die Leitfähigkeit von einem sehr großen auf einen kleineren Wert ändert oder umgekehrt. Schematisch werden die Verhältnisse in der Graphik gezeigt. Diese Situation könnte auch an den Klemmen der Stromquelle eintreten. Am Ende des Widerstands, der nahe am positiven Pol liegt, bildet sich demnach eine schmale positive Raumladungswolke aus, am "negativen" Ende, eine negative. Durch die beiden Raumladungen entsteht ein zusätzlicher Beitrag zum elektrisches Feld, das im Widerstand größer sein muss, um bei gleicher Stromdichte den Effekt der verminderten Leitfähigkeit auszugleichen. Eine quantitative Untersuchung finden Sie hier.

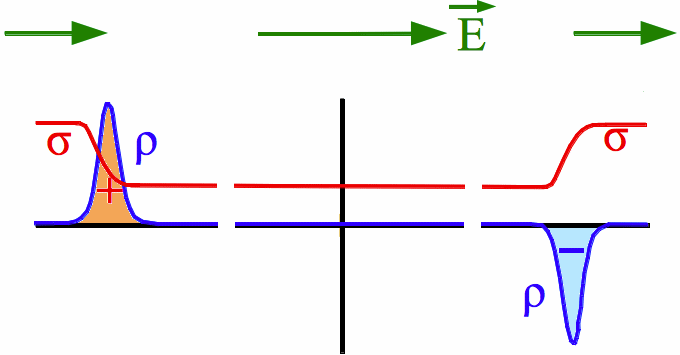Abb. 2a: Die Leitfähigkeit σ soll hier im Widerstand  kleiner als im Rest des Stromkreises sein. Die Zeichnung zeigt die Polarität der Stirnladungen zur Anpassung der elektrischen Feldstärke E. Im Widerstand ist die elektrische Feldstärke (Pfeillänge) größer als im Rest des Stromkreises. Die Tendenz "E-Feld außerhalb der Batterie von + nach - gerichtet" wird beibehalten.

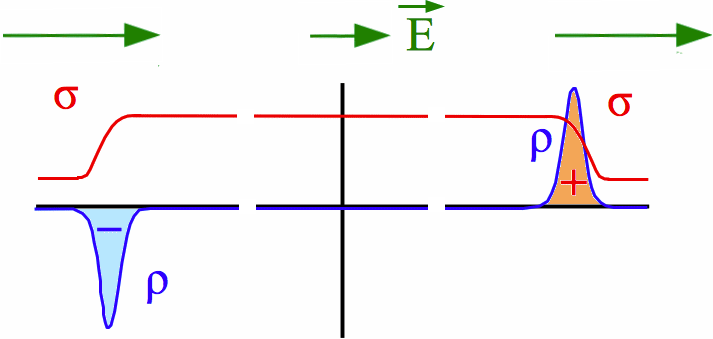Abb. 2b: Die Leitfähigkeit σ im "Widerstand" soll hier größer sein als im Rest des Stromkreises. Die Raumladungen zur Anpassung der elektrischen Feldstärke E haben umgekehrtes Vorzeichen wie in Abb. 2a. Im "Widerstand" ist die elektrische Feldstärke kleiner als im Rest des Stromkreises (Pfeillänge). Die Tendenz "E-Feld außerhalb der Batterie von + nach - gerichtet" wird beibehalten. Das bestätigt erneut, dass die Raumladungen nur zur Anpassung des elektrischen Felds dienen, nicht zur Erzeugung des elektrischen Felds, das von der Batterie ausgeht und in beiden Zeichnungen von links nach rechts gerichtet ist. Man könnte allenfalls sagen, dass die Raumladungen ein Zusatzfeld erzeugen, das hier entgegengesetzt zum äußeren Feld (von der Batterie) her gerichtet ist, und das in der Überlagerung (Addition) ein geschwächtes Gesamtfeld im "Widerstand" ergibt. (beide Zeichnungen schematisch)

Auch im "Druckmodell" des geschlossenen Wasser-Stromkreises (Heizungskreislauf) kommt der Druckunterschied an Engstellen nicht durch unterschiedliche Wassermengen oder Wasserdichten vor und nach der Engstelle zustande. Tatsächlich muss man den dynamischen Druck einbeziehen. Ohne Strömung herrscht (bei mehreren Engstellen) überall der gleiche Druck (abgesehen vom evtl. vorhandenen Schweredruck). Erst bei Strömung bilden sich Druckdifferenzen vor und nach Engstellen aus.

Das Druckmodell ist aus verschiedenen Gründen problematisch: Welcher Schüler (und welcher Lehrer) kennt sich schon in der Strömungslehre aus? Der Schweredruck kann dabei offensichtlich überhaupt keine Rolle spielen, weil sich das Wasser unter seiner Wirkung nicht bewegt, sondern allein wegen der Pumpenwirkung. Welche Rolle spielen bei der Entstehung eines Druckgefälles etwa Turbulenzen? Änderung der Leitfähigkeit könnte veränderten Turbulenzen entsprechen?

3. Wie sind nun die Verhältnisse an der Übergangsstelle zwischen einer galvanischen Zelle und dem restlichen Stromkreis?

Im Inneren der Zelle gilt  j = σ_i · (E  + E^(e)). Dabei ist E^(e) ein formales Wirbelfeld (rot E^(e) ≠ 0; rot E = 0), das die chemischen Kräfte innerhalb der Zelle charakterisiert. Es heißt oft "eingeprägtes Feld" (siehe EMK). Es verschwindet überall außerhalb der Zelle; deswegen rot E^(e) ≠ 0. σ_i ist die Leitfähigkeit im Inneren der Zelle. Aus div j = 0 folgt div ( σ_i · (E  + E^(e) )) = 0 , und damit gemäß (*):

(**)               (E^(e) + E) · (grad  σ_i )    =   - σ_i · div ( E^(e)+ E )

Wenn (E^(e) + E) = 0 im Inneren (linke Seite = 0), z.B., weil kein Strom fließt (Leerlauffall), oder wenn kein Innenwiderstand vorhanden ist ( σ_i => unendlich), sind die Quellen von E zugleich formal die Senken von E^(e) und umgekehrt:  " E^(e) erzeugt das Feld E ".  Durch die im Übergangsbereich zwischen Innen und Außen erzeugten Quellen von E wird dieses auch in den Außenraum fortgesetzt, aber so, dass das ohmsche Gesetz und die Kontinuitätsgleichung eingehalten wird.

Wenn (E^(e) + E) ≠ 0 , gibt es Quellen von E^(e) + E,  also Ladungsanhäufungen (rechte Seite von (**)  ≠ 0), nur dort, wo sich die Leitfähigkeit im Inneren ändert (grad  σ_i ≠ 0) .

4. Die Verhältnisse in einem Gleichstromkreis mit einer galvanischen Zelle stellen sich damit folgendermaßen dar:

Chemische Kräfte im Inneren der galvanischen Zelle sorgen für eine Ladungstrennung. Sie lassen sich formal beschreiben durch ein Wirbelfeld E^(e). Sie, bzw. E^(e), erzeugen ein wirbelfreies Feld E, das sich in den Raum außerhalb der galvanischen Zelle fortsetzt. Es stellt sich bei einem stationären Strom so ein, dass es trotz der dissipativen Kräfte in den Widerständen zeitlich konstant ist, bei Stromfluss dem ohmschen Gesetz genügt und natürlich der Kontinuitätsgleichung.

Das elektrische Feld E ist also sowohl eine Folge der chemischen Kräfte als auch der dissipativen Kräfte in den Widerständen und des Stroms, die sich auch im ohmschen Gesetz äußern.

Das ist also ganz anders als in der Elektrostatik. Dort ist ein Feld vorgegeben. Eventuell bewegen sich einzelne Ladungen entsprechend diesem vorgegebenen Feld. Beim stationären Strom stellen sich Feld und Strom erst ein gemäß der Stromdichte, der Widerstände und der Stromquelle. Ein Beispiel soll das erläutern:

Früher wurden Van-der-Graaf-Generatoren eingesetzt um Elektronen auf einige MeV zu beschleunigen. Problem war, dass das elektrische Feld in der Nähe der Konduktoren coulombartig war mit unter Umständen sehr großen elektrischen Feldstärken, so dass viele Ladungen vorzeitig abgesprüht wurden. Deshalb wurde angestrebt, das elektrische Feld zu linearisieren. Das gelang mit einer Kette von sehr großen Widerständen längs des Gummibands zwischen beiden Konduktoren. Durch sie floß zwar ein sehr kleiner Strom, aber mit überall konstanter Stromdichte j. Gemäß des ohmschen Gesetzes  j = σ · E musste sich auch die elektrische Feldstärke E überall konstant einstellen: Der Strom, die Widerstände und die elektrostatischen Eigenschaften des Generators bestimmten das elektrische Feld!

Außerhalb der galvanischen Zelle gibt es nur dieses elektrische Feld E. Da es wirbelfrei ist, ist es - trotz des Stromflusses - (formal) ein Potenzialfeld. Die Widerstände im Stromkreis haben deshalb über die Stromdichte j bei Stromfluss Einfluss auf die Ortsabhängigkeit von E und das zugehörige "Potenzialfeld" (im Außenraum der galvanischen Zelle).

Bei fehlendem Strom (unterbrochener Stromkreis) bzw. wenn die Stromquelle keinen Innenwiderstand besitzt, heben sich beide Felder, E und das formale E^(e) , bzw. die zugehörigen Kräfte im Inneren der galvanischen Zelle im Idealfall ganz auf.

Ob es sinnvoll ist, ausgehend vom "Potenzialfeld" E für Ladungen eine potenzielle Energie zu definieren, ist fraglich. (Beachten Sie, dass E nur einen Teil der wirkenden Kräfte vermittelt und sich mit dem stationären Strom erst einstellt!). Es ist ja wohl plausibel, dass die chemischen Kräfte in der Zelle Energie freisetzen. Ob daraus aber potenzielle Energie einzelner Ladungen wird oder z.B. elektrische Feldenergie, möge der Leser selbst entscheiden. Die Frage ist auch weitgehend belanglos: Aus den energetischen Vorgängen beim stationären Strom fallen E und eine daraus konstruierte potenzielle Energie insgesamt völlig heraus. Nur E^(e) bzw. die chemischen Kräfte, die es symbolisiert, haben Einfluss auf die energetischen Vorgänge. Außerdem ist die definierende Eigenschaft eines Potenzials, die Wegunabhängigkeit, hier nur außerhalb der galvanischen Zelle gegeben. Man kann zeigen, dass für eine Verschiebung von einem Punkt P₁ zu einem Punkt P₂ unterschiedliche Verschiebungsarbeiten benötigt werden, je nachdem, ob die Verschiebung durch die galvanische Zelle führt oder nicht. Bei gleicher Ausgangsenergie für die Ladung am Ort P₁ ergäben sich dann für unterschiedliche Wege unterschiedliche Endenergien am gleichen Ort P₂, recht untypisch für eine potenzielle Energie der Ladung am Ort P₂, aber typisch für nichtkonservative Kräfte!

Im geschlossenen Stromkreis mit einem stationären Strom gibt es also zwei Arten nichtkonservativer Kräfte: die chemischen Kräfte und die dissipativen Kräfte. Energetisch ist es klar: die Arbeit, die die chemischen Kräfte in der Stromquelle freisetzen, ist genau die, die die dissipativen Kräfte in Wärme umsetzen. Auch bei der Entladung eines Kondensators, wo - ohne Stromfluss - ein Potenzialfeld existiert, wirken bei Stromfluss nichtkonservative, nämlich dissipative, Kräfte.

Die meisten dieser Überlegungen muss man in der Schule verschweigen. Was man mit den Schülern aber erarbeitet, sollte der Theorie nicht widersprechen.

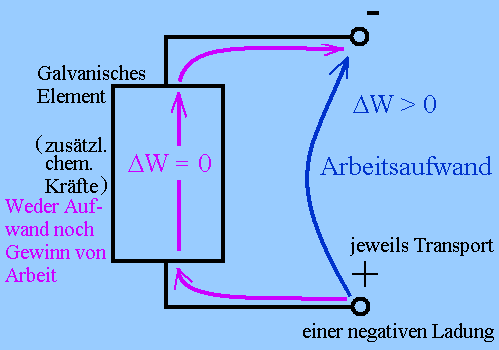Abb. 3: Bei Verschiebung einer negativen Ladung von P1 nach P2 im Außenraum eines galvanischen Elements (oder einer anderen Stromquelle) ist Arbeitsaufwand nötig, nicht dagegen für eine Verschiebung zwischen den gleichen Punkten, wenn die Verschiebung durch das galvanische Element hindurch erfolgt. In diesem Fall heben sich die chemischen Kräfte und die elektrische Abstoßungskraft dort ungefähr auf. Trotz gleichen Anfangs- und Endpunkts der Verschiebung ist die Verschiebungsarbeit unterschiedlich. Es lässt sich - streng genommen - keine potenzielle Energie als Funktion des Orts allein definieren.

Anmerkung: Es wäre interessant, ob sich ein mechanisches Gravitations-/Höhenmodell für die Verhältnisse beim stationären Strom konstruieren ließe, bei dem - entsprechend der Situation hier - durch das Zusammenwirken von Pumpe, Stromdichte und Strömungswiderständen das Gravitationsfeld ähnlich angepasst werden könnte wie hier das elektrische Feld. Vermutlich ist das nicht möglich, weil hier das Feld E von der Pumpe (und ... ) erst erzeugt wird, während dort das Gravitationsfeld vorgegeben ist.

5. Verhältnisse bei der Induktion

Bei der Induktion in einem Stromkreis ohne eigene Stromquelle entsteht ein Wirbelfeld mit rot E = - ∂B/∂t. Wenn es ein reines Wirbelfeld ist (div E = 0), kann es sowieso keine Ladungsanhäufungen geben.

Hier könnte der ringförmig geschlossene homogene Leiter als Prototyp genommen werden mit einem zeitabhängigen Magnetfeld B; bei Gültigkeit des ohmschen Gesetzes    j = σ · E  müsste überall div E = 0 sein; damit sind gestaute Ladungen überall ausgeschlossen, auch aus Symmetriegründen. Dennoch gibt es ein elektrisches (Wirbel-) Feld und eine Ringspannung (aber mit Sicherheit keine Spannung im Sinn einer Potenzialdifferenz).

Wie eben erläutert, könnten sich Ladungsdichten ρ höchstens dann aufbauen, wenn sich die Leitfähigkeit der geschlossenen Induktionsschleife oder -Spule irgendwo ändert.

.

6.  Änderung des Querschnitts A des Leiters

Ändert sich allerdings der Querschnitt A des Leiters, dann ist j (mit dem Betrag j = I/A; bei konstantem I) wie auch E bestenfalls abschnittsweise konstant. (Aha: j bestimmt E!) (Auch, wenn die Leitfähigkeit σ nur abschnittsweise konstant ist, kann E nur abschnittsweise konstant sein.)

Ist in diesem Fall (variabler Querschnitt A, aber konstante Leitfähigkeit σ) div E und damit auch ρ  an den "Kontaktstellen" von 0 verschieden? Dann würde es hier also Ladungsanhäufungen geben.

Die Stromstärke I im unverzweigten Stromkreis ist überall gleich. Wenn sich bei sonst gleichen Bedingungen der Querschnitt von A₁ auf A₂ ändert, ändert sich die Stromdichte von j₁ auf j₂ = j₁·A₂/A₁. Hinter der Kontinuitätsgleichung steckt aber die Ladungserhaltung:   div j +  ∂ρ/∂t  = 0. Da  ∂ρ/∂t  = 0 bei einem stationären Strom - es gibt schließlich keine Produktion oder Vernichtung von Ladungen im Volumenelement ΔV - , gilt div j  = 0 : Alle Ladungen, die in ein Volumenelement ΔV hineinströmen, müssen auch wieder herausströmen.