© Horst Hübel Würzburg
2005 - 2014
Der rechteckige leitende Ring, der sich über den Schenkel eines Hufeisenmagneten bewegt - ein Paradebeispiel für die Induktion |
Der Aufsatz richtet sich an Lehrer, nicht an Schüler.
Hier wird noch eine Standardaufgabe aus der Schulphysik untersucht: Ein geschlossener Leiterring gleitet über die Schenkel eines Hufeisenmagneten.
a) Wie wird der Vorgang in der Schule beschrieben?
b) Was sagen verschiedene Formen des Induktionsgesetzes nach dem Wikipedia-Artikel zur "Elektromagnetischen Induktion" dazu? Ich gehe hier davon aus, dass die dort angegebenen beiden Formen des Induktionsgesetzes zwar beide gleichzeitig gültig, aber nicht gleichwertig sind, da sie evtl. unterschiedliche physikalische Informationen enthalten.
b) Qualitativ: Gibt es hier eine Änderung des magnetischen Flusses durch den Leiterring, wie es bei der Induktion charakteristisch ist?
 |
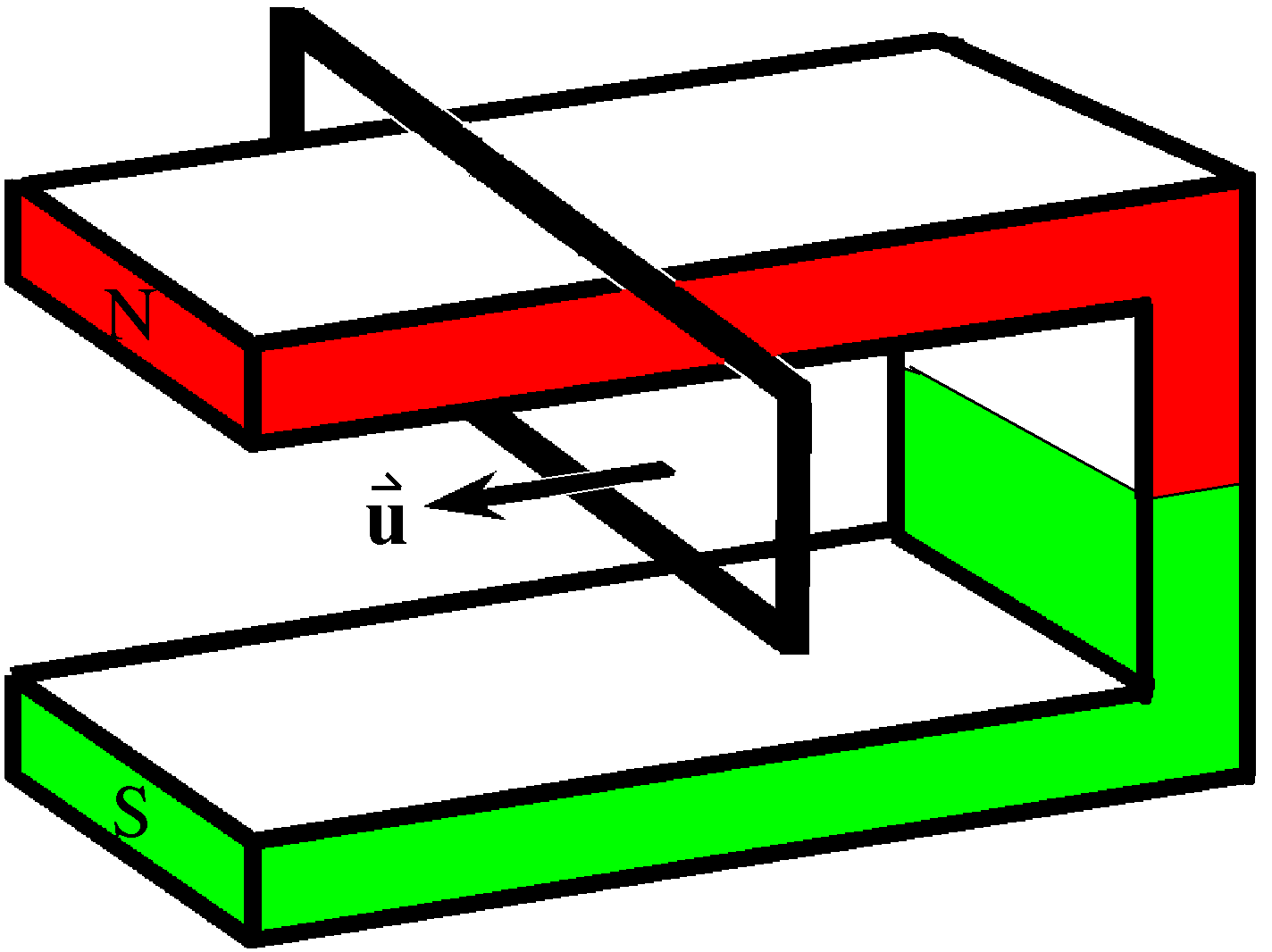
Der Ring soll sich mit konstanter Geschwindigkeit u längs eines Schenkels des Hufeisenmagneten mit zeitlich konstantem Magnetfeld bewegen. Seine Ebene soll stets senkrecht zu den Schenkeln verlaufen. Zwischen den Schenkeln soll das Magnetfeld homogen sein und B senkrecht u; dort soll das Magnetfeld immer parallel zur Ringebene und senkrecht zu einem Leiterstück verlaufen. Die anderen drei Leiterstücke des Rings sollen sich in einem vernachlässigbaren Magnetfeld bewegen. |
a) Auf Schulniveau ist die Aufgabe mit einem Trick leicht zu lösen:
Es wird im Bezugssystem des ruhenden Magneten diskutiert. Es wirkt eine Lorentz-Kraft in dem Leiterstück L1 senkrecht zum Magnetfeld im Zwischenraum und senkrecht zur Bewegungsrichtung (u). In den anderen drei Leiterstücken ist eine Lorentz-Kraft vernachlässigbar. Die Lorentz-Kraft treibt einen konstanten Ringstrom an, solange die Geschwindigkeit konstant ist. Es muss eine Ringspannung wirken.
Dieser Gesichtspunkt wird in der Schule außer acht gelassen, indem der Leiterring unterbrochen bzw. mit einem hochohmigen Spannungsmesser ergänzt wird. Dann besteht die einzige Wirkung der Lorentz-Kraft darin, im Leiterstück L1 eine Ladungsverschiebung zu bewirken. An einem Pol sammeln sich positive, am anderen negative Ladungen. Je mehr Ladungen verschoben werden, desto größer ist das (statische) elektrische Feld E, das sich als Folge der Ladungsverschiebung im Leiter aufbaut. Der Aufbau des elektrischen Feldes ist beendet, wenn Kräftegleichgewicht zwischen der Lorentz-Kraft und der sich ausbildenden elektrischen Kraft herrscht, also, wenn (für die Beträge)
e·E = e·u·B
Durch das Auftrennen des Leiters hat man das erreicht; darin besteht der Trick. Das elektrische Feld im Leiter ist homogen, deswegen kann wie im idealen Plattenkondensator die (gewöhnliche) Spannung zwischen beiden Polen berechnet werden:
U = E·ℓ = B·v·ℓ (wenn ℓ die Länge des Leiterstücks L1 ist)
E ist dabei das sekundäre, statische elektrische Feld, nicht das elektrische (Wirbel-)Feld, das primär durch die Induktion zustande kommt. Mit Recht nimmt man an, dass diese statische Spannung (Potenzialdifferenz) von gleicher Größe wie die Ringspannung ist, die man dann auf jeden Fall braucht, wenn der Leiterring geschlossen ist, wenn also ein Ringstrom fließt und es diese Potenzialdifferenz nicht mehr gibt. Für ihn gilt bei einem Gesamtwiderstand R: I = U/R = B·v·ℓ / R.
b) Qualitativ: Gibt es hier eine Änderung des magnetischen Flusses durch den Leiterring, wie es bei der Induktion charakteristisch ist?
Setzen wir uns in den Leiterring ("mitbewegtes BZS"). Bei der Bewegung ändert sich das Magnetfeld, das den Leiterring senkrecht durchsetzt (vor allem im umfassten Schenkel des Magneten, nicht zwischen den Schenkeln). Der Leiterring kann nicht entscheiden, ob die Änderung von einer zeitlichen Änderung von B herkommt oder von räumlichen Änderungen von B. Zeitliche Änderung des magnetischen Flusses führt zu einem elektrischen Wirbelfeld längs des Leiterrings und dieses zu einer Ringspannung.
Jetzt sollen die Integralformen IForm I und IForm II des Induktionsgesetzes nach dem Wikipedia-Artikel angewandt werden und zwar einmal im BZS des ruhenden Magneten und ein zweites Mal im BZS des Leiterrings.
Hinweis: ∫o bedeutet Ringintegral über einen geschlossenen Weg.
Der Wikipedia-Artikel "Elektromagnetische Induktion" stellt neben der differenziellen Form zwei Integralformen vor. Beide sind richtig, machen aber u.U. unterschiedlich umfasssende physikalische Aussagen zur Induktion. Die Integralform (IForm) I ist sicher äquivalent zur differenziellen Form. Die ebenfalls richtige IForm II macht dagegen u.U. weitergehende Aussagen und ist deshalb nicht äquivalent zur IForm I. Alle drei Formen des Induktionsgesetzes müssen ergänzt werden durch eine Angabe, wie sie mit einer messbaren Größe zusammenhängen, mit der Induktionsspannung U. Die Induktionsspannung ist in jedem Fall eine Ringspannung, keine Potenzialdifferenz. Manche Autoren spalten sie auf in einen "Bewegungsanteil" UM, der mit der Lorentz-Kraft zusammenhängt, und einen "transformatorischen Anteil" UT, der von einer expliziten Zeitabhängigkeit der magnetischen Flussdichte B herrührt. Die gesamte Induktionsspannung U ist die Summe aus beiden Anteilen: U = UM + UT. Ausgehend von der IForm II ( ∫o (E + u x B)·dl = - d/dt Φ ) sind beide Anteile erkennbar:
UT = ∫o E·dl und UM = ∫o (u x B)·dl
In IForm I ist UM nicht erkennbar. Wenn die magnetische Flussdichte B zeitlich konstant ist, folgt aus IForm I nur: Es gibt kein elektrisches Wirbelfeld, UT = 0. Will man also die gesamte Induktionsspannung angeben, muss man sich den Anteil UM auf eine andere Weise besorgen, wobei in der Regel die Lorentz-Kraft bemüht wird, manchmal auf eine mehr oder weniger problematische Weise. Noch einmal: Auch der Anteil UM ist eine Ringspannung. Der Zusammenhang des Spannungsbegriffs mit der Verschiebungsarbeit kann dies auch elementar begründen. Argumentiert man von einem einheitlichen Bezugssystem aus, in dem E und B gemessen werden, erscheinen "Bewegungsinduktion" und "transformatorische Induktion" als zwei grundverschiedene Erscheinungen. Dagegen gibt es andere BZSe, von denen aus Induktion als ein einheitliches Phänomen erscheint: Entstehung eines elektrischen Wirbelfelds längs einer geschlossenen Kurve C bei einer zeitlichen Änderung des magnetischen Flusses innerhalb der von C eingeschlossenen Fläche.
.
d) BZS des ruhenden Magneten (Felder E und B):
Hinweis: ∫o bedeutet Ringintegral über einen geschlossenen Weg.
IForm I: ∫o E·dl = 0 => In diesem BZS entsteht kein elektrisches Wirbelfeld E, da B nicht zeitabhängig ist. Damit weiß man noch nicht allzuviel über die Induktion und nichts über die Induktionsspannung. Für sie braucht man ein eigenes Argument. Auch, wenn man die Lorentz-Kraft jetzt ins Spiel bringt, kommt man zu einer nicht verschwindenden Ringspannung, wenn man die verallgemeinerte Definition der Ringspannung über Arbeit pro Ladung ins Spiel bringt.
IForm II: ∫o (E + u x B)·dl = - d/dt Φ , also, da ∫o (E ·dl ) = 0,
UR = - ∫o ( u x B )·dl entsprechend der elementaren, schulischen Herleitung, wobei dort aber nicht klar wird, dass eine Ringspannung vorliegt.
Bei dieser Wahl des BZS liefert erst die IForm II Wesentliches zur Induktion. Im Wikipedia-Artikel wird stattdessen bei IForm I die Induktion durch ein ohmsches Gesetz ins Spiel gebracht, aber geleugnet, dass eine Ringspannung entstehe.
Wenn als BZS das des ruhenden Magneten gewählt wird, enthält IForm I offenbar noch nicht die Induktion. Sie muss von außen hinzugefügt werden, z.B. durch expliziten Gebrauch der Lorentz-Kraft und des Kräftegleichgewichts (so etwas steckt beim "ohmschen Gesetz" des Wikipedia-Artikels dahinter). Sie ist erst in IForm II ganz enthalten.
e) BZS des ruhenden Leiterrings (Felder E' und B' = B in guter Näherung):
Vom Leiterring aus gesehen ist das Magnetfeld B' zeitabhängig => elektrisches Wirbelfeld längs des Leiterrings.
Formal: Bei Bewegung ist die Änderungsrate δB'/δt im bewegten BZS (B ruht im anderen BZS) :
δB'/δt = dB'/dt + rot ( u x B') (*)
Dabei enthält die Flussdichteänderung Anteile durch die überstrichene, vom Magnetfeld durchsetzte Fläche (2. Term, hergeleitet aus Geometrie und div B = 0; siehe beliebiges Lehrbuch der theoretischen Elektrodynamik mit den dort angegebenen Präzisierungen. Die Quellenfreiheit des B-Feldes (div B = 0) erzwingt den Bewegungs-Term, der auf eine Lorentz-Kraft zu verweisen scheint!).
IForm I: ∫o E'·dl = = - d/dt Φ = - Integral δB'/δt ·dA =/= 0 => In diesem BZS entsteht ein elektrisches Wirbelfeld E', da B' zeitabhängig ist, und damit eine nicht verschwindende Ringspannung. Die rechte Seite lässt sich mit (*) berechnen und es entsteht IForm II ((*) steht m Zusammenhang mit dem totalen magnetischen Fluss, der sich bei der Bewegung des Leiterrings ändert):
IForm II: ∫o E'·dl = ∫o (E + u x B)·dl
Für die Ringspannung UR gilt hier auch UR = ∫o E'·dl = ∫o (E + u x B)·dl = ∫o (u x B)·dl , da B nicht explizit zeitabhängig bzw. E = 0
Wenn als BZS das des ruhenden Leiterrings gewählt wird, zeigt bereits IForm I, dass Induktion entstehen muss. Zur genaueren Berechnung muss man die Änderungsrate von B' berechnen. Das Ergebnis ist die IForm II. Nur in diesem Fall sind beide IFormen gleichbedeutend, in jedem Fall aber gleichzeitig gültig. Diese Wahl des BZS ist deshalb auch sympathisch, weil hier keine (wie oben behebbaren) Schwierigkeiten entstehen bzgl. des Zusammenhangs mit der Ringspannung.
.
f) Induktion "im magnetisch abgeschirmten Leiter"
T. wies darauf hin, dass "Bewegungs-Induktion" auch dann entsteht, wenn der bewegte Teil des Leiterrings magnetisch abgeschirmt ist, so dass keine Lorentz-Kraft wirken kann.
Im BZS des ruhenden Leiterrings kann die Argumentation von e) voll übernommen werden. Induktion findet statt, weil sich der vom Leiterring eingeschlossene magnetische Fluss zeitlich ändert (und zwar vor allem im überstrichenen Schenkel des Hufeisenmagneten). Induktion ist ein nichtlokaler Effekt!
Im BZS des ruhenden Hufeisenmagneten ist die Argumentation nicht ganz so offensichtlich. Nach wie vor ist UT = 0. Aber woher kommt UM =/= 0?. Eine Lorentz-Kraft sollte nicht entstehen.