|
Definition eines
Koordinatensystems im realen Raum
|
Vielleicht haben die Schüler in der einführenden Stunde erfahren, dass
eine der bahnbrechenden Erkenntnisse Galileis die Methode war, Bewegungen
in vereinfachten, idealisierten Situationen zu untersuchen.
Jetzt beginnt also die Mechanik mit eindimensionalen Bewegungen und dann
ganz konkret mit der Definition eines Koordinatensystems im Klassenzimmer,
in dem eine Bewegung studiert werden soll (vgl. SG001.html)
 |
Sonarmeter CBL von Texas Instruments / Vernier, was
offenbar funktionsgleich zu dem von PASCO ist (nicht zu
verwechseln mit CBR, das direkt an TI-Taschenrechner angeschlossen
wird, das deshalb für das PC-Programm SONAR nicht verwendet werden
kann). Es sendet auf Kommando einen Ultraschall-Impuls aus und
nimmt das Echo auf. Es liefert ein Rechteckssignal, dessen
High-Phase die Laufzeit des Signals widerspiegelt.
Die Schüler lernen zunächst einen "elektronischen Zollstab"
kennen, der mit Hilfe von Ultraschall-Signalen Entfernungen
misst. Die für die Schule geeignete Variante, das Sonarmeter,
mit einem geeigneten PC-Programm (hier: SONAR) wird
ihnen vorgestellt.
Zunächst in digitaler Anzeige sehen die Schüler die
sich verändernden Abstände eines hin- und herlaufenden Schülers
vom Sonarmeter.
|
Dann wird also das Koordinatensystem definiert. Der Bauchnabel
eines Schülers im Strahl des Sonarmeters wird zum Zentrum der Welt
erklärt. Im Programm SONAR wird durch Tastendruck die momentane
Position zum Ort 0 gemacht und alle anderen Abstände darauf bezogen.
Der Schüler begibt sich in eine Position mit der Anzeige 1 m, 2 m, 3 m,
... . Die Positionen werden, z.B. mit Kreide auf dem Fußboden, markiert.
Der Schüler begibt sich zurück zum Koordinatenursprung und dann über
diesen hinaus: die Anzeige wird negativ. Zumindest der Ort - 1 m wird
markiert. Damit ist augenfällig klargeworden, wie ein Koordinatensystem im
Prinzip konstruiert wird, was negative Orte bedeuten, wie willkürlich ein
Koordinatenursprung und eine positive Richtung festgelegt werden. Denn
wieder durch Tastendruck lässt sich die Koordinatenrichtung auch umkehren,
bei den früheren 2 m wird jetzt - 2 m angezeigt.
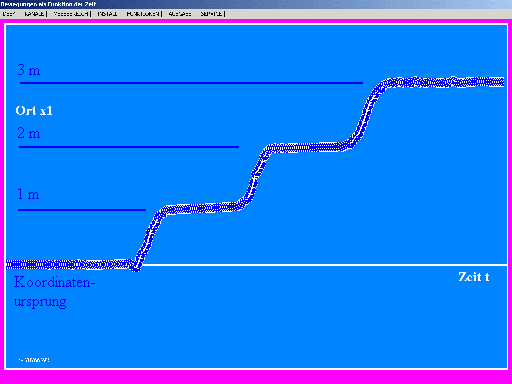 |
Dann wird auf Graphik-Anzeige umgeschaltet, auf dem
Bildschirm erklärt, wie jetzt das Koordinatensystem auf dem
Bildschirm erscheint, was die zusätzliche Zeitachse ist. Es werden
möglichst einfache Realbewegungen des Schülers oder
Lehrers gezeigt. Der Proband hat den Auftrag, zunächst schnell von
Meter-Position zu Meter-Position zu wechseln, dort aber etwas
anzuhalten. An der entstehenden Treppenfunktion erkennen die
Schüler, wie ein bestimmter Ort auf dem Bildschirm erscheint. Auch
ein negativer Ort sollte so visualisiert werden. Die Schüler
lernen es, einfache Bewegungs-Graphen auf dem Bildschirm
zu interpretieren, d.h. in Beziehung zu setzen zur beobachteten
Bewegung. |
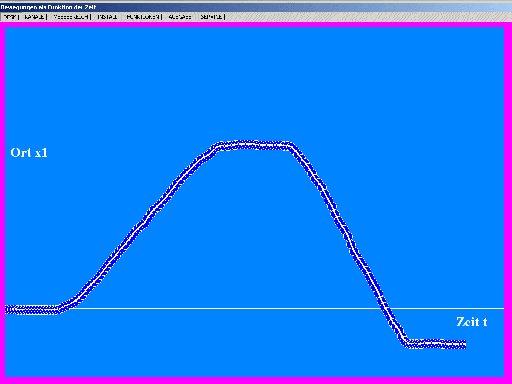 |
Dann erhält der Proband den Auftrag, möglichst mit konstanter
Geschwindigkeit in positive Richtung zu laufen, eine
Zeitlang anzuhalten, dann wieder rückwärts zu laufen. Die Schüler
verfolgen auf dem Bildschirm mit, wie der Ort "gleichmäßig" größer
und kleiner wird.
Ob der Vorgriff sinnvoll ist, dass das gleichzeitig
mitgemessene t-v-Diagramm jetzt schon gezeigt und entschlüsselt
wird, möge der Lehrer selbst entscheiden. Die Schüler würden
jetzt schon lernen:
Negative (positive) Geschwindigkeit bedeutet eine Bewegung in
Richtung der negativen (positiven) Ortsachse, und: konstante
Geschwindigkeit bedeutet lineare Veränderung des t-x-Diagramms.
|
| M.E. hat man damit die Voraussetzung geschaffen, dass in den
Schülern die Notwendigkeit verankert wird, vor jeder Bewegung
ein Koordinatensystem zu entscheiden, und dass diese
Entscheidung willkürlich ist (man kann also nichts falsch
machen).
Mit dem Sonarmeter gerät der Lehrer auf keinen Fall in
Versuchung, die Bewegung durch "Wege" zu beschreiben, weil immer
(positive und negative) Koordinaten gemessen werden.
t-x-Diagramme statt der t-s-Diagramme sind hier
selbstverständlich. Das überholte und häufig irreführende
"Weg-Konzept" wird hier nicht unterstützt.
Die Schüler machen das erste Mal Erfahrungen im Lesen
einer graphischen Bewegungs-Darstellung, indem sie den
Zusammenhang zwischen einer Realbewegung im Koordinatensystem
und ihrer graphischen Darstellung studieren.
|
In späteren Situationen kann es sinnvoll sein, den Koordinatenursprung
und die positive Richtung durch aufgestellte Hinweisschilder zu
visualisieren.
Bei der Einführung der harmonischen Schwingung wird der
Koordinatenursprung in die Ruhelage des Pendels gelegt. Dann ist es völlig
natürlich, dass die Ortskoordinate x eine direkte Bedeutung für die
Schwingung hat, nämlich als "Auslenkung" (Elongation), und dass die
Ortskoordinate x im Laufe der Zeit unterschiedliche Vorzeichen erhält. Es
lässt sich sogar zeigen, sollte aber zunächst verschwiegen werden, dass
bei einem hängenden Pendel der Koordinatenursprung somit in der durch die
Gewichtskraft verschobenen Ruhelage liegt, so dass eine Gewichtskraft oder
eine Lageenergie in Zukunft außer acht gelassen werden kann.
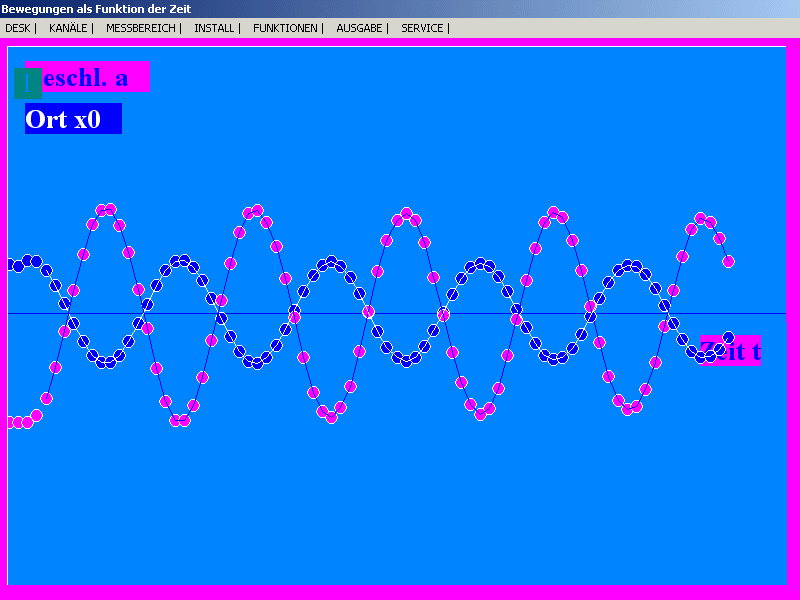 |
Ortskoordinate x bzw. Auslenkung und Beschleunigung a
bei einer harmonischen Schwingung. Der Koordinatenursprung x = 0
wird definiert als die Ruhelage.
Auslenkung und Beschleunigung wurden hier im Realversuch
mit einem Sonarmeter im Unterricht am Friedrich-Koenig-Gymnasium
Würzburg gemessen. |
.
.



