Strahlt man einen dünnen Strahl monochromatischen Röntgenlichts der Wellenlänge λ auf einen Streukörper z.B. aus dem Metall Zr, dann kann man zwei unterschiedliche Erscheinungen bei den austretenden Röntgenstrahlen beobachten:

(1) Ein mehr oder weniger geradeaus durchgehenden Röntgenstrahl hat unveränderte Wellenlänge λ; sie soll hier nicht betrachtet werden.

(2) Auch unter einem Ablenkungswinkel θ  tritt Röntgenstrahlung aus. Sie hat gegenüber λ vergrößerte Wellenlänge λ'. Die Wellenlängenänderung ∆λ = λ' -  λ ist umso stärker, je größer der Ablenkungswinkel θ ist. Auch die Intensität der abgelenkten Röntgenstrahlung ist vom Ablenkungswinkel θ abhängig. Dieser abgelenkte Anteil der austretenden Röntgenstrahlung heißt Compton-Strahlung.

Für sie müssen drei Dinge erklärt werden:

(1) Wie kommt es überhaupt zu der winkelabhängigen Wellenlängenänderung?

(2) Wie kann man die Größe der Winkelabhängigkeit erklären?

(3) Welcher Gesetzmäßigkeit genügt die Intensität der Compton-Strahlung?

Bei der letzten Frage geht es offenbar um die Wahrscheinlichkeit, mit der Compton-Strahlung unter einem bestimmten Winkel θ  abgelenkt wird.

Zur Erklärung der ersten beiden Fragen wurde folgendes Modell^*) gemacht:

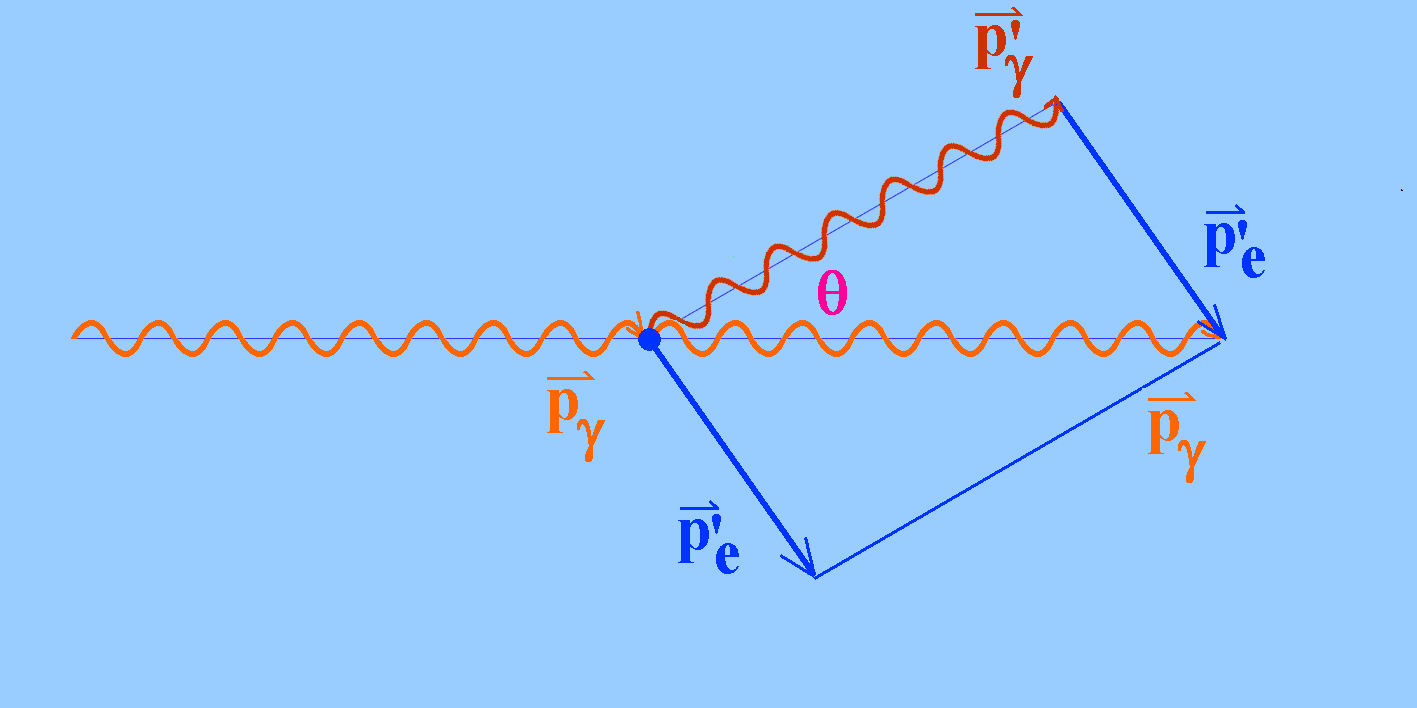
Aus Energie-Erhaltungsgründen muss neben dem ein- und austretendem Photon mindestens ein weiterer Partner beteiligt sein. Dafür boten sich Elektronen an, die im Streumaterial nur leicht gebunden sind. Näherungsweise werden sie als freie Elektronen angesehen. Wenn man das Photonenbild des Lichts anwenden will, bietet sich die Vorstellung eines Stoßes zwischen einem einfallenden γ-Photon mit Energie E_γ und Impuls p_γ an und einem ruhenden Elektron. Da die Energie der Röntgenphotonen in der Größenordnung von 100 keV sehr viel größer als die Ruheenergie der Elektronen ist, war eine relativistische Rechnung nötig. Für das ursprüngliche Elektron muss dann die Ruheenergie E_e,0 berücksichtigt werden. Die beiden austretenden Teilchen sind dann ein Photon mit veränderter Energie E_γ' und verändertem Impuls p_γ' und ein Elektron mit der Energie E_e'. Die Dynamik des Stoßes kann man mit dem Energie- und dem Impulserhaltungssatz (EES und IES) gemäß der Abbildung erfassen:

(1)  EES:                    E_γ   + E_e,0  =   E_γ'  +   E_e'         (wobei  E_γ = p_γ · c und  E_γ'  = p_γ' · c  und  E_e'² =  E_e,0²  +  p_e'² · c²  )

(2)  IES:                      p_γ  =    p_γ'  +  p_e'                     (mit den jeweiligen Impulsvektoren)

Nach Umformungen hat man 3 Gleichungen für die 4 Variablen θ, p_γ, p_γ' und p_e', die sich mit etwas Algebra lösen lassen.

Es ergibt sich die Compton-Formel:

∆λ = λ - λ' =   λc [ 1 - cos(θ) ]    mit der Compton-Wellenlänge  λc = h/(me,0.c) **)

Wenn θ = 0^o (keine Ablenkung) kommt es auch nicht zu einer Wellenlängenänderung. Bei θ = 90^o ist die Wellenlängenänderung gleich der Compton-Wellenlänge λ_c. Die größte Wellenlängenänderung erhält man für θ = 180^o (Rückwärtsstreuung), wo die Wellenlängenänderung gleich der doppelten Compton-Wellenlänge ist.

Die nach dem Modell berechnete Wellenlängenänderung stimmt mit den Beobachtungen sehr gut überein. Dies gilt als eine weitere Bestätigung der Vorstellung vom Licht als eines Stroms von Photonen. Nicht erfasst wird durch das Modell die Wahrscheinlichkeit für die Ablenkung eines Photons unter einem bestimmten Winkel. Dazu braucht man die richtige Quantentheorie.

^*) Es gibt auch ein klassisches Modell des Compton-Effekts. Es beruht auf dem Doppler-Effekt. Die damit errechnete Wellenlängenverschiebung stimmt aber nicht mit den Beobachtungen überein.

^**) h ist dabei das Plancksche Wirkungsquant, m_e,0 die Ruhemasse des streuenden Elektrons und c die Vakuumlichtgeschwindigkeit. Eine Wellenlängenverschiebung erhält man auch mit klassischen Wellen, wenn man den Doppler-Effekt berücksichtigt, allerdings nicht quantitativ.

.