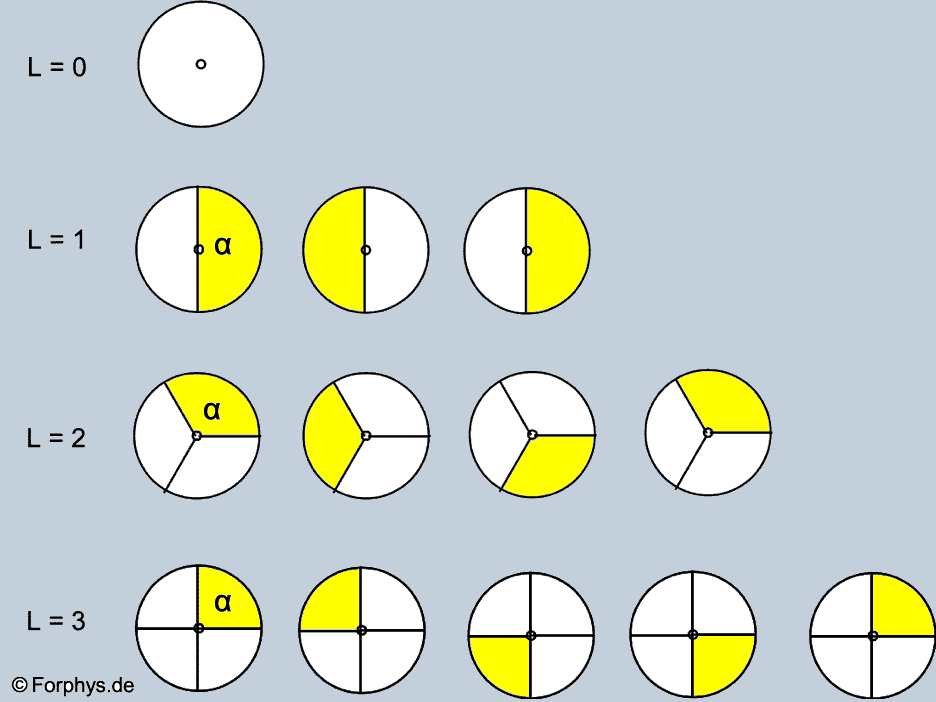
Nach L+1 Teildrehungen wird wieder die Ausgangssituation erreicht
|
G05 Drehimpuls |
Neben Impuls, Energie oder Ladung ist der Drehimpuls eine weitere Erhaltungsgröße. Sie ist eine vektorielle Größe, die mit der "Rotationsinvarianz" zusammenhängt, also der Invarianz gegenüber räumlichen Drehungen. Während der Drehimpuls eines starren Körpers (z.B. eines Zylinders) vom Trägheitsmoment Θ und der Winkelgeschwindigkeit ω abhängt und damit bei Variation von Θ und ω jeden beliebigen Wert annehmen kann, ist der Drehimpuls eines Quantenobjekts "gequantelt", kann also jeweils nur bestimmte Werte annehmen, die von einer Drehimpuls-Quantenzahl L abhängen.
Was bedeutet Rotationsinvarianz? Man kann das nach Abb. 1 in einer 2-dimensionalen Situation geometrisch verstehen. Dabei wird eine Kreisfläche bzw. der Vollwinkel 2·π nacheinander in verschiedene Teile L+1 gleichmäßig aufgeteilt, wobei L = 1, 2, 3, ... Es entstehen Kreissektoren mit (Teil-)Winkeln α = 2·π/(L+1). Erst nach einer Rotation in L+1 Schritten um insgesamt dem Winkel α·(L+1) (um das Zentrum) kann die gedrehte Figur mit der ursprünglichen Figur zur Deckung gebracht werden.
 |
Abb. 1: Rotationssymmetrie Nach L+1 Teildrehungen wird wieder die Ausgangssituation erreicht |
Rotationsinvariante (rotationssymmetrische) Funktionen sind z.B. auch A(α) = ½·r2·α·L für die Kreissektor-Fläche, ψ(α) = cos(α·L) oder Wellenfunktionen der Quantenphysik (L = 1, 2, 3 ... ). Das erste Mal wird hier nach L "Teildrehungen" um den Winkel α eine volle Drehung erreicht, wenn α·L = 2·π, also mit den Teilwinkeln α = 2·π/L.
In der relativistischen Quantenmechanik wurde entdeckt, dass auch L = 1/2 in der Natur realisiert ist. Üblicherweise heißt L dann Spinquantenzahl S. Dann erhält man das erste Mal nach einer zweifachen Voll-Drehung Deckung. Das steht im Zusammenhang mit dem Spin als relativistischem Effekt.
Beispiel einer rotationssymmetrischen Funktion*) für S = 1/2 ist f(α) = cos(α·S). Das erste Mal wird hier eine volle Drehung erreicht, wenn α·S = 2·π , also nach einem Drehwinkel α = 2·π/S = 4·π.
| α | cos(α·S) |
| 0 | 1 |
| π | 0 |
| 2·π | -1 |
| 3·π | 0 |
| 4·π | 1 |
Man unterscheidet zwischen den Quantenzahlen für Bahndrehimpuls L, Spin S und Gesamtdrehimpuls J. Der Gesamtdrehimpuls ist aus Bahndrehimpuls und Spin zusammengesetzt.
*) In der relativistischen Quantenmechanik müssen gewöhnliche (1-komponentige) Wellenfunktionen durch 4-komponentige Spinoren ersetzt werden, die - grob gesagt - Eigenschaften von Elektronen und ihren Antiteilchen (Positronen) enthalten. 4-komponentige Spinoren ähneln 4-dimensionalen Spaltenvektoren.