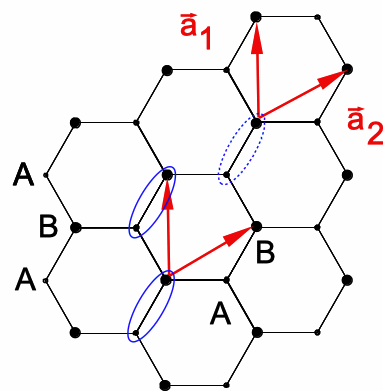
Abb.1: Graphen-Struktur aus einem dreieckigen Gitter, wobei jeder Gitterpunkt mit einer Basis aus 2 Atomen belegt ist (Ellipsen).
|
|
Kreuzgitter-Interferenz, z.B.
beim Wabengitter von Graphen |
Bemerkungen (1) zum Artikel von M. Rode, „Beugung an zweidimensionalen Gittern als Modell für die Elektronenbeugung“ im MNU journal 04, 2022, S. 309
In dem Artikel untersucht der Autor, ob der Streukörper in schulüblichen Elektronenbeugungsröhren so beschaffen ist, dass Kristallgitter-Interferenz an einem Graphit-Gitter, oder dass Kreuzgitter-Interferenz an einer ebenen Honigwaben-Schicht von C-Atomen stattfindet. Im ersten Fall müsste Bragg-Reflexion an einem Raumgitter eingesetzt werden, im zweiten Fall Kreuzgitter-Interferenz wie bei Graphen ("Grafeeen" gesprochen). Der Autor entscheidet sich aufgrund eines Experiments mit Röntgenstrahlen für Kreuzgitter-Interferenz.
Er benutzt dazu kommentarlos eine Formel, die wie die Formel für Doppelspalt- bzw. Strichgitter-Interferenz in 1. Ordnung aussieht (sin(δ) = λ/d; von mir „Rode-Formel“ genannt), wobei d aber nicht die Gitterkonstante (Spaltabstand), sondern der Netzlinienabstand sein soll. λ ist die Wellenlänge. Tatsächlich gibt es in der Honigwabenschicht keine C-Atome im Abstand d. Der verwirrende Sachverhalt soll hier geklärt werden.
Die gewöhnliche Bragg-Reflexion von Röntgen- oder Elektronenstrahlung lässt sich unter verschiedenen Gesichtspunkten sehen:
Als „Bragg-Reflexion, aber keine Reflexion“. Die Bragg-Beziehung 2d·sin(α) = n·λ entscheidet, bei welchem Glanzwinkel α so etwas wie Reflexion stattfindet, wobei d der zugehörige Netzebenenabstand ist und n die Ordnung des Reflexes. Bezogen auf den Wellenvektor des einfallenden Strahls k0 erfolgt dann eine Ablenkung um einen Winkel δ = 2·α. Der Wellenvektor des austretenden Strahls k und der Wellenvektor des einfallenden Strahls k0 schließen also den Winkel δ ein. Weitgehend unabhängig von der Belegung der Netzebenen scheinen diese wie ein einheitliches Ganze zu wirken.
Als Folge von Beugung und Interferenz an den (evtl. komplex belegten) Gitterpunkten. Das beschreibt die Laue-Theorie, mit Hilfe derer sich die Bragg-Beziehung herleiten lässt. Sie begründet auch, weshalb Reflexion nur bei bestimmten Glanzwinkeln stattfindet.
Als eine Folge der Impulserhaltung bei Einbeziehung möglicher Gitterimpulse (in der Festkörperphysik werden sie häufig als Quasiimpulse bezeichnet): Vom Wellenzahlvektor k kommen wir durch Multiplikation mit ħ zum Impuls (der Photonen oder der Elektronen), analog vom Vektor der Wellenzahländerung ∆k zum Gitterimpuls ∆p: p = p0 + ∆p. Charakteristisch ist, dass das Gitter nur bestimmte Gitterimpulse ∆p aufnehmen oder abgeben kann. Die Laue-Theorie zeigt, dass für ∆k = ∆p/ħ nur die reziproken Gittervektoren infrage kommen, die von der Gitterstruktur abhängen. Diese stehen senkrecht auf parallelen Netzebenen in einem Abstand d, und man kann die Bragg-Beziehung anwenden, ohne die Belegung der Netzebenen mit streuenden Körpern im Detail zusätzlich zu berücksichtigen. Das gesamte System der parallelen Netzebenen scheint zusammen zu wirken und die bestimmten Gitterimpulse zu ermöglichen.
Ähnlich können wir auch die Kreuzgitter-Interferenz an einem ebenen Kreuzgitter sehen, das durch Überlagerung zweier regelmäßiger Punktgitter zustande kommt, die einen Winkel ε miteinander einschließen. Das Kreuzgitter soll senkrecht durchstrahlt werden, wobei also der Wellenzahlvektor k0 des einfallenden Strahls immer senkrecht zur Ebene des Kreuzgitters steht.
In jedem der beiden Punktgitter gibt es periodische Strukturen in einem Abstand d' (Gitterkonstante), die „spektrentragende“ Geraden (senkrecht zur Einfallsrichtung) definieren. Für eine bestimmte Wellenlänge λ sind dann Interferenz-Maxima unter Winkeln δ' gegenüber den „spektrentragenden“ Geraden zu finden, für die gilt sin(δ') = n·λ/d' (n ganze Zahl), wie beim Doppelspalt und beim Strichgitter. Anders als dort liegen sie auf Kegeln mit dem Öffnungswinkel δ' mit der „spektrentragenden“ Geraden als Achse. Sichtbar sind nur die Maxima auf den Schnittpunkten der beiden Kegelsysteme. Das ist also eine ziemlich unübersichtliche Situation.
Aber auch beim Kreuzgitter gilt die Impulserhaltung bzw. die entsprechende Relation für die Wellenzahlvektoren: p = p0 + ∆p bzw. k = k0 + ∆k. p und p0 wie auch k und k0 schließen den Ablenkungswinkel δ ein. Wiederum zeigt die Laue-Theorie von Beugung und Interferenz an einem ebenen Gitter, dass für die Vektoren ∆k ausschließlich reziproke Gittervektoren infrage kommen, die sich aus der Geometrie des Gitters ergeben. Das erklärt schon qualitativ, dass bei der senkrechten Durchstrahlung des ebenen Gitters ein System von mehr oder weniger punktförmigen Reflexen entstehen, die sich um den einfallenden Strahl als Symmetrieachse gruppieren. Die Laue-Theorie lehrt, welche Ablenkungswinkel auch in diesem Fall entstehen. In der Literatur, bei Rode und in Lehrplänen findet man stattdessen den Vorschlag, den Winkel δ' mit der „Rode-Formel“ zu berechnen. Dabei ist allerdings nicht von vornherein klar, dass die hier anzuwendende Gitterkonstante d' der Netzlinienabstand (gemessen senkrecht zu den „spektrentragenden“ Geraden) und dass der Winkel δ' der Ablenkungswinkel ist. In der Formel für Strichgitter-Interferenz ist jedenfalls d' die Periodenlänge längs einer „spektrenbildenden“ Geraden und nicht der Netzlinienabstand d.
Um diese Diskrepanz zu klären, soll hier - sich auf die Ausführungen zur Laue-Theorie im Festkörperphysik-Buch von Kittel [Ki 1968] stützend - der Ablenkungswinkel δ für die Gitterstruktur von Graphen berechnet werden, also für Kreuzgitter-Interferenz. Graphen besteht aus einer ebenen Schicht miteinander verbundener Sechsecksringe. Die Struktur wird üblicherweise [Tr 2007] beschrieben als ein Verbund von zwei Sorten von Kohlenstoff-Atomen, die ein Sechseckssystem besetzen (Abb. 2, 3). Sie werden zu einer zweiatomigen „Basis“ aus einem Paar von A- und B-Atomen verbunden, die sich durch entgegengesetzte Bindungsrichtungen unterscheiden. Die Basen besetzen die roten Punkte eines Dreieckssystems (Abb. 2, 3). Die Bindungen zwischen den beiden Atomen des Paars sind alle gleich orientiert.
 |
Abb.1: Graphen-Struktur aus einem dreieckigen Gitter, wobei jeder Gitterpunkt mit einer Basis aus 2 Atomen belegt ist (Ellipsen). |
Als Gittervektoren werden a1 und a2 mit den Beträgen 2·d2 (d2 = 123 pm) gewählt (Abb. 1, 2). Ein zweidimensionales kartesisches Koordinatensystem kann z.B. so orientiert werden, dass a1 in y-Richtung zeigt und a2 dazu unter 600 geneigt, also a1 = 2·d2·(0|1|0) und a2 = d2·(√3|1|0).
|
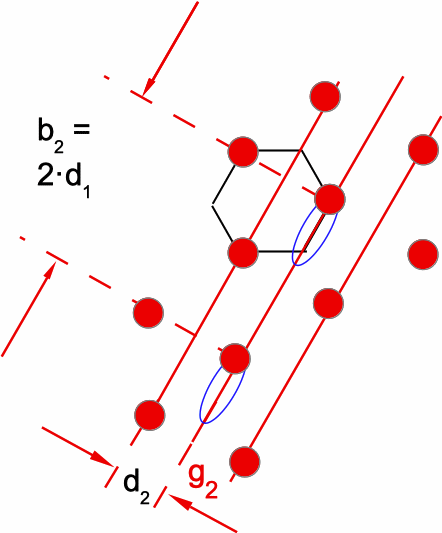
Abb. 2: Definition der Netzlinien vom Typ 1 (senkrecht zum reziproken Gittervektor A1) mit Abstand d2 bei einer Periode b2 = 2·d1 |
|
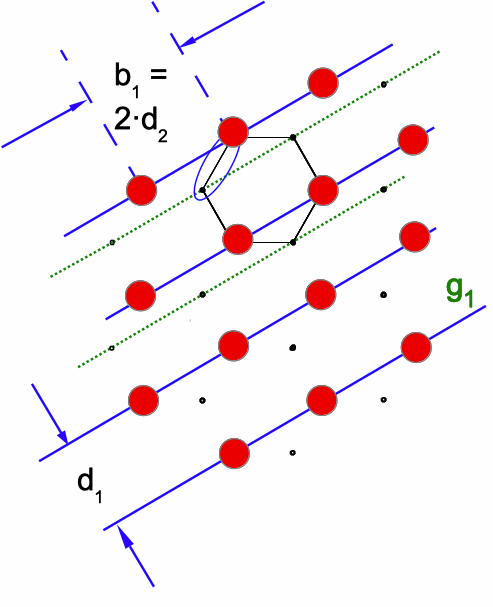
Abb.
3: Definition der Netzlinien vom
Typ 2 (senkrecht zu A1
+
A2·)
mit Abstand d1
bei
einer Periode b1
=
2d2
|
Die zugehörigen Vektoren des reziproken Gitters erfüllen folgende Bedingungen:
(1) A1·a2 = A2·a1 = 0 (Orthogonalität) und (2) A1·a1 = A2·a2 = ± 2π (Interferenz-/ Maximumsbedingung). Es lässt sich zeigen, dass beide Gleichungen durch den Ansatz erfüllt werden:
A1 = π/d1·(1|-√3|q) und A2 = 2π/d1·(1|0|p). Die z-Koordinaten q und p sind zunächst noch unbestimmt. Ihre Festlegung erfordert weitere Bedingungen. Ein allgemeiner reziproker Gittervektor hat die Form G = r·A1 + s·A2 (r, s ganze Zahlen).
Für den Wellenzahlvektor k der austretenden Welle gilt k = k0 + G, wobei k0 der Wellenzahlvektor der in z-Richtung einfallenden Welle ist. Beschränken wir uns auf den Fall r = 1 und s = 0. Dann erhalten wir für k: k = 2π/λ·(0|0|1) + π/d1·(1|-√3|q) = 2π/λ·(0|0|1) + 2π/λ · f/2 ·(1|-√3|q) = 2π/λ ·(f/2|-f/2√3|1+f·q/2) mit dem Betrag |k| = 2π/λ·√[f2 + (1+ f·q/2)2] und der Abkürzung f = λ/d1.
Jetzt nutzen wir eine weitere Bedingung zur Festlegung der z-Komponente. Wir verlangen nämlich, dass der Stoß elastisch erfolgt, also |k| = |k0|, dass eintretende und austretende Welle gleiche Wellenlänge haben. Dann folgt √[f2 + (1+ f·q/2)2] = 1 und (1+ f·q/2)2 = 1 – f2, also q = - 2/f ± 2ß/f, wobei ß = √[1 - f2]
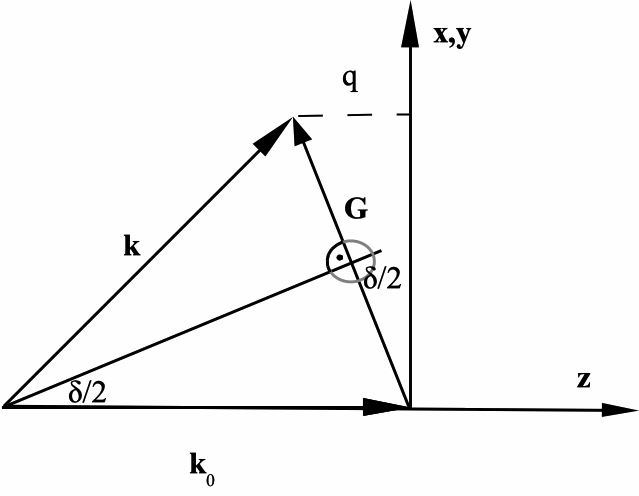
Für q gibt es zwei Lösungen, die unterschiedliche Vorzeichen enthalten. Wie zu erwarten war, ist A1 bzw. G etwas aus der x-y-Gitterebene heraus gegen die Richtung der einfallenden Welle geneigt, damit das Vektordiagramm von Abb. 4 erfüllt werden kann. Damit ergibt sich schon eine Deutungsmöglichkeit für q: Elementargeometrisch folgt nach Abb. 4, wie q von δ/2 abhängig ist.
Für den Betrag des Impulsübertrags ∆p = ħ·A1 erhalten wir |A1| = 2π/λ·f/2·√[1 + 3 + q2] = 2π/λ·√[f2 + {-1 ± ß}2] = 2π/λ·√[2 ± 2ß], also nach Abbildung 4:
|
Abb. 4: Orientierung von Wellenzahlvektoren k, k0 und reziprokem Gittervektor G. G steht senkrecht auf einem Vektor des realen Gitters, z.B. a1. Das Kreuzgitter liegt in der x-y-Ebene.
|
sin(δ/2) = 0,5·|A1|/|k0| = √[1/2 ± ß/2] = √[ ½ ± ½·√(1 - f2)]
Nur für einen Fall (Minuszeichen) berechnen wir δ numerisch und erhalten mit λ = 154 pm und d1 = 213 pm: δ = 46,30, wie es auch Rode vorhergesagt hat. Das Ergebnis gilt für beliebige f = λ/d1, solange Interferenz stattfindet.
Das Ergebnis überrascht, da es tatsächlich auch mit der „Rode-Formel“ gewonnen werden kann: sin(δ') = λ/d1 = f liefert δ' = 46,30, obwohl es bei der vorgegebenen Graphen-Struktur keine periodischen Strukturen im Abstand d1 gibt, wie es für die Strichgitter-Formel notwendig wäre, tatsächlich überhaupt keine im Abstand d1. Allenfalls findet man periodische Strukturen im Abstand 2·d1 bzw. 2·d2. Zudem erscheint es ziemlich willkürlich, dass δ' als Ablenkungswinkel beim ebenen Gitter interpretiert werden sollte. Eine stichhaltige physikalische Begründung, weshalb hier die Doppelspalt- bzw. Strichgitter-Formel anwendbar ist und ein korrektes Ergebnis liefert, fiel mir nicht ein.
Aber die Äquivalenz lässt sich mathematisch beweisen: Trigonometrisch gilt schließlich in einem geeigneten Winkelbereich für den halben Winkel sin(δ'/2) = √[0,5·(1-cos(δ')] = √{0,5·(1-√[1-sin2(δ')]} Das ist genau der Ausdruck der Laue-Theorie für sin(δ/2), wenn sin(δ') mit f = λ/d1 identifiziert wird. Also der zunächst unklare Winkel δ' ist tatsächlich der Ablenkungswinkel. Aus Symmetriegründen liefert A2 das gleiche Ergebnis.
Mit r = s = 1 erhält man entsprechend: sin(δ) = λ/d2 .
Folgerung: Ähnlich wie man bei der Bragg-Reflexion für bestimmte Glanzwinkel α so tun kann, als werde die einfallende Strahlung an Netzebenen im Abstand d1 bzw. d2 reflektiert, kann man bei der senkrechten Durchstrahlung eines ebenen Kreuzgitters so tun, als gäbe es beugende Kristallbauteile in den (Netzlinien-)Abständen d1 bzw. d2, und als verhalte sich das System dabei wie ein Strichgitter mit diesen Gitterkonstanten. Der von Rode berechnete Ablenkungswinkel ist also korrekt und erlaubt dessen weitergehende Entscheidungen bezüglich der Struktur des Streukörpers.
Interferenz an der zweiatomigen Basis und Beugung an den Atomen fügt der Intensitätsverteilung weitere Strukturfaktoren hinzu. Weil deren Dimensionen kleiner sind als die Netzlinienabstände kann man Auslöschungen durch Interferenz höchstens in höheren Ordnungen erwarten. Kleinere Ablenkungswinkel sind nicht zugelassen, da kein erlaubter Vektor des reziproken Gitters dazu passt, oder anders: da es keinen geeigneten Gitterimpuls für die Impulserhaltung dabei gibt.
Die Bragg-Reflexion ist in der Schulphysik relativ einfach zu verstehen. Eine Analyse nach der Laue-Theorie ist für sie ausgeschlossen. Wenn man unbedingt die Formel für Strichgitter-Interferenz verwenden möchte, sollte man nicht nach Periodizitäten suchen und auch nicht fragen, wie der Winkel δ einzuzeichnen ist. Es bleibt das heuristische Argument, dass auch mit der „Rode-Formel“ die richtigen Ablenkungswinkel erhalten werden. Wie mag es wohl gelingen, die Schüler/innen davon zu überzeugen?
Einen
Versuch dazu finden Sie hier,
der ähnliche Schwächen aufweist wie die schulische Herleitung der
Formel für die Bragg-Reflexion.
Rode kann wohl - nach persönlicher Mitteilung - mit seinem „geschickten Werkzeug“ (Geogebra) den Rode-Winkel δ = 46,30 numerisch für wenige C-Atome in der Sechsecks-Struktur reproduzieren, den er auch für Röntgenstrahlen mit λ = 154 pm gemessen hat.
Literatur
[Ki 1968] Ch. Kittel, Einführung in die Festkörperphysik, R. Oldenbourg Verlag, München (1968), S. 79
[Tr 2007] B. Trauzettel, Von Graphit zu Graphen, Physik Journal 6 (2007), S. 40