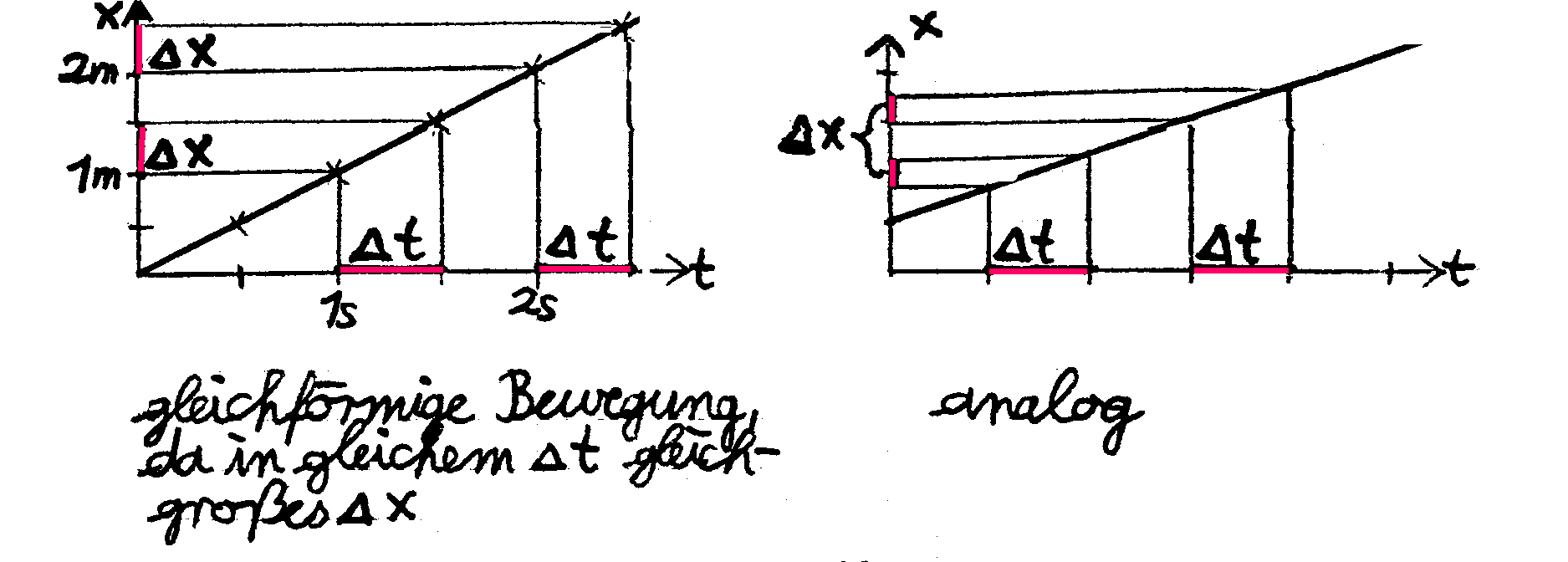Es liegt nahe, die positive Koordinatenrichtung entsprechend der Bewegungsrichtung zu wählen. Wird der Ort x (die Ortskoordinate) in Abhängigkeit von der Zeit aufgetragen, erkennt man, dass in gleichgroßen Zeitabschnitten Δt gleichgroße Ortsänderungen Δx erfolgen.

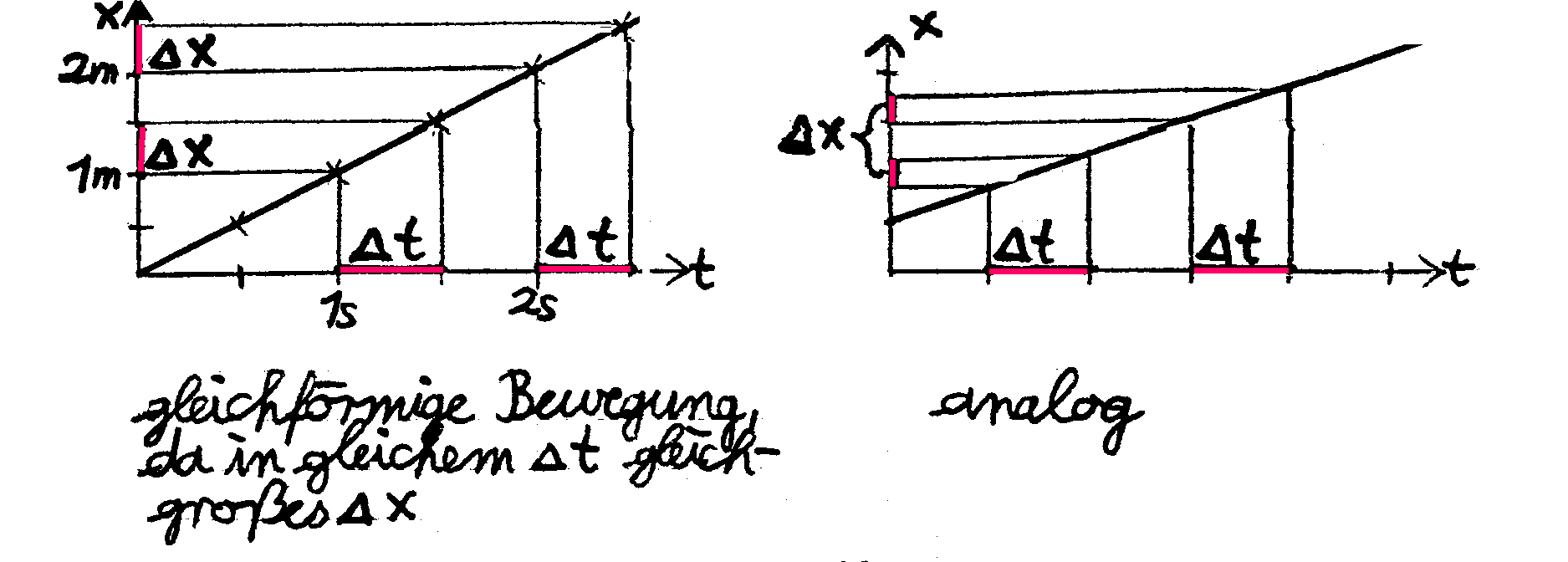Aus einem Schülerheft: eindimensionale Bewegung; der Vektorcharakter des Ortsvektors ist durch das Vorzeichen der Ortskoordinate x erfasst. Der Anfangsort x0 ist links 0, also der Koordinatenursprung. Rechts ist x0 > 0. Die Geschwindigkeit ist dort - unmittelbar einsichtig - kleiner als links.

Das führte ursprünglich zur Definition der Geschwindigkeit

Da allgemein (für evtl. sehr kleine Zeitabschnitte Δt) gilt

liegt bei der gleichförmigen Bewegung der Spezialfall vor: Beschleunigung a = 0.

Wenn der Zeitabschnitt Δt zur Zeit 0 beginnt, kann man auch schreiben:

x₀ ist dabei der Anfangsort , v₀ oder v die konstante (Anfangs-)Geschwindigkeit. Das t-x-Diagramm zeigt eine Gerade, die eine Ursprungsgerade ist, wenn der Anfangsort 0 ist. v ist in jedem Fall die Steigung des t-x-Diagramms.

Das t-v-Diagramm zeigt eine Konstante. Die Fläche unter der t-v-Diagramm entspricht der Ortsänderung Δx = v·Δt . Diese Überlegung ist eine Grundlage des "Flächenverfahrens".

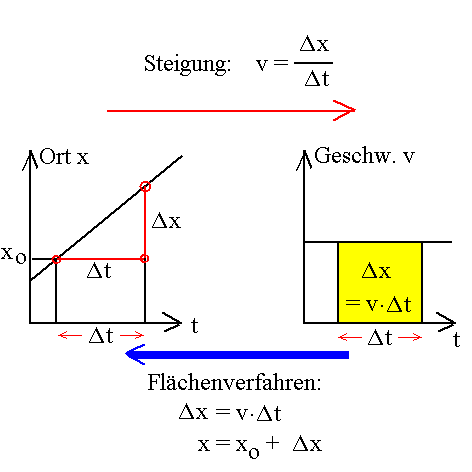Vom Ort x zur Geschwindigkeit v mittels der Steigung. Von der Geschwindigkeit v zum Ort x mittels des Flächenverfahrens bei bekanntem Anfangsort x0.

.

( Setember 2013 )