Ein einfaches Beispiel für die Anwendung der Methode der kleinen Schritte:

Ein Fallschirmspringer lässt sich in der Regel aus dem Flugzeug fallen, wobei er zunächst bei geschlossenem Fallschirm quasi einen freien Fall durchführt. Er erreicht dann nach einiger Zeit eine Geschwindigkeit v₀. Jetzt zieht er die Reißleine, der Fallschirm öffnet sich - wir nehmen an: schlagartig - und jetzt beginnt ein gebremster Fall. Dieser allein soll hier untersucht werden.

Der Koordinatenursprung wird an den Ort des plötzlichen Öffnens des Fallschirms gelegt; v₀ wird als Anfangsgeschwindigkeit genommen. Die positive Koordinatenrichtung soll nach unten gerichtet sein. Es wirken zwei Kräfte: die Gewichtskraft mit dem Betrag m·g nach unten, also in positive Richtung, und die Luftreibungskraft mit dem Betrag k·v² nach oben, in negative Richtung. Als Kraftgesetz gilt insgesamt F = m·g - k·v². m ist die Masse des Springers inkl. Fallschirm, g die Fallbeschleunigung, k eine Konstante, die die Größe des Luftwiderstands bestimmt zusammen mit dem Quadrat der Geschwindigkeit.

Vorüberlegungen:

a) Es gibt eine Endgeschwindigkeit v_end. Wenn nämlich bei einer bestimmten Geschwindigkeit die Beschleunigung 0 wird, bleibt v konstant und die Gesamtkraft verschwindet. Es gilt also:

F = m·g - k·v_end²  = 0 , also  v_end² = m·g/k

b) Solange v₀ ≦ v  < v_end , überwiegt in der Gesamtkraft die Gewichtskraft. F ist positiv (F also nach unten gerichtet). Der Überschuss F sorgt für eine weitere Zunahme der Geschwindigkeit, bis v_end  erreicht ist.

c) Wenn aber v₀ ≧ v  > v_end , überwiegt in der Gesamtkraft die Luftwiderstandskraft. F ist negativ (F also nach oben gerichtet) und bremst den Fall, bis v = v_{end .}

Nach Erreichen der Endgeschwindigkeit erfolgt eine gleichförmige Bewegung.

Berechnung

Mit Hilfe der Methode der kleinen Schritte wird die Bewegung jetzt näherungsweise berechnet. Die Kraft F = m·g - k·v² bestimmt im Kausalkettenschema die Beschleunigung a = F/m = g - k/m·v² . Sie wird für jedes kleine Zeitintervall Δt als konstant angesehen. Daraus ergibt sich dann für jedes Zeitintervall die Geschwindigkeit v = v₀ + a·Δt und der Ort x = x₀ + v₀·Δt + 1/2· a·Δt². Die errechneten Werte dienen für das nächste Zeitintervall als Anfangswerte.

Die folgenden Graphen zeigen Geschwindigkeit und Beschleunigung in Abhängigkeit von der Zeit für die Parameter m = 70 kg ,  k = 120 kg/m . Die Rechnung wurde mit einem Tabellenkalkulationsprogramm durchgeführt. (Positive Koordinatenrichtung nach unten).

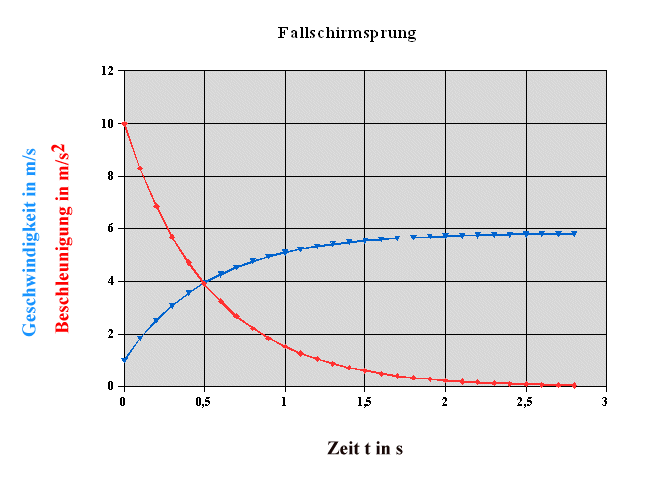
Start mit Anfangsgeschwindigkeit 1 m/s. Es wird schließlich eine Geschwindigkeit von ca. 6 m/s erreicht. Bei der geringen Anfangsgeschwindigkeit überwiegt zunächst die Gewichtskraft nach unten. Die Beschleunigung (rot) ist positiv (nach unten gerichtet). Mit zunehmender Geschwindigkeit wächst auch die Luftreibungskraft nach oben. Im Gleichgewicht heben sich beide Kräfte gegenseitig auf: a ist 0 und v konstant.

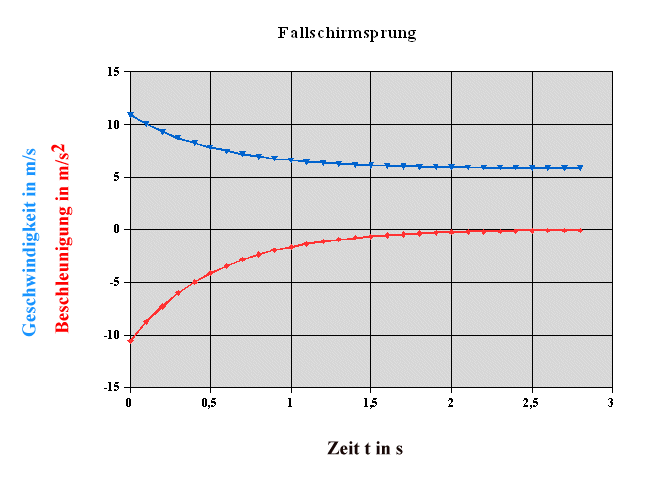
Start mit Anfangsgeschwindigkeit 11 m/s. Es wird schließlich ebenfalls eine Geschwindigkeit von ca. 6 m/s erreicht. Bei der großen Anfangsgeschwindigkeit überwiegt zunächst die Luftreibungskraft nach oben. Die Beschleunigung (rot) ist negativ (nach oben gerichtet). Mit abnehmender Geschwindigkeit nimmt auch die Luftreibungskraft ab. Im Gleichgewicht heben sich beide Kräfte gegenseitig auf: a ist 0 und v konstant.

Die Graphen bestätigen die Vorüberlegungen.

.

( September 2013 ; November 2020: präzisierende Ergänzungen)