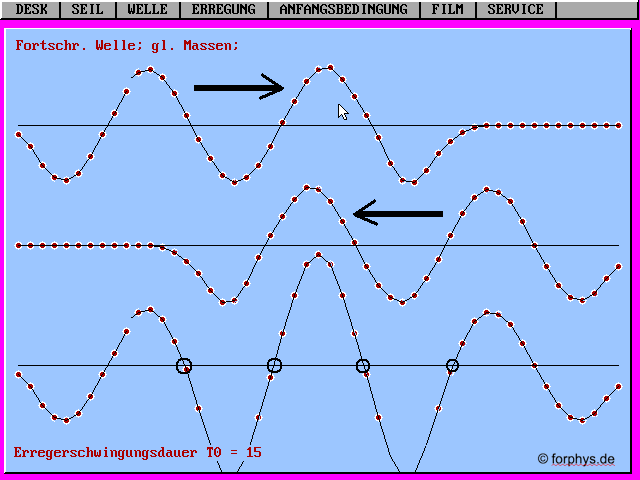
Abb. 1: Eine nach rechts laufende Welle und eine nach links laufende Welle überlagern (addieren) sich.  Es entstehen feste Knoten und Bäuche (3. Zeile). Wenn die beiden Wellen im Laufe der Zeit fortschreiten, verändern sich die Knoten (eingeringelt) nicht. An den Knoten herrscht ständige Ruhe. Dagegen schwingen die roten Pendelkugeln zwischen zwei Knoten heftig auf und ab.  An den Bäuchen herrscht maximale Bewegung. Bildschirmfoto erstellt mit dem Programm WELLEN.exe des Autors für eine durch elastische Federn gekoppelte Kette von Pendelkugeln (lineare Pendelkette)

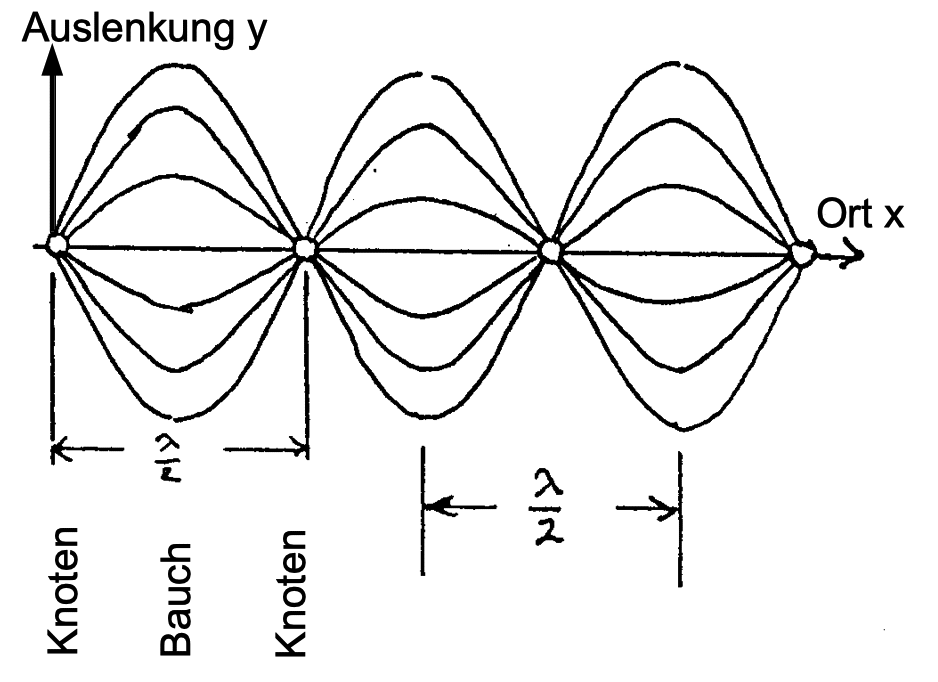Abb. 2: Knoten und Bäuche längs der x-Achse (Ortsachse) zu verschiedenen Zeitpunkten. Wenn die Pendelkugeln nicht schwingen, ruhen sie auf der Ortsachse. Das ist die "Ruhelage". Pendelkugeln in den Knoten ruhen immer. Außerhalb der Knoten schwingen die Pendelkugeln immer wieder durch die Ruhelagen hindurch. An der Stelle der Bäuche haben die Pendelkugeln zu manchen Zeiten die größte Auslenkung. Benachbarte Knoten haben einen Abstand von λ/2, genauso wie benachbarte Bäuche.

Die zwei entgegen laufenden Wellen gleicher Frequenz (Kreisfrequenz 𝜔) und Wellenlänge λ kann man auch dadurch erreichen, dass man z.B. eine nach rechts laufende Welle reflektieren lässt, etwa an einer Wand. Die entstehende nach links laufende Welle überlagert sich dann mit der nach rechts laufenden.

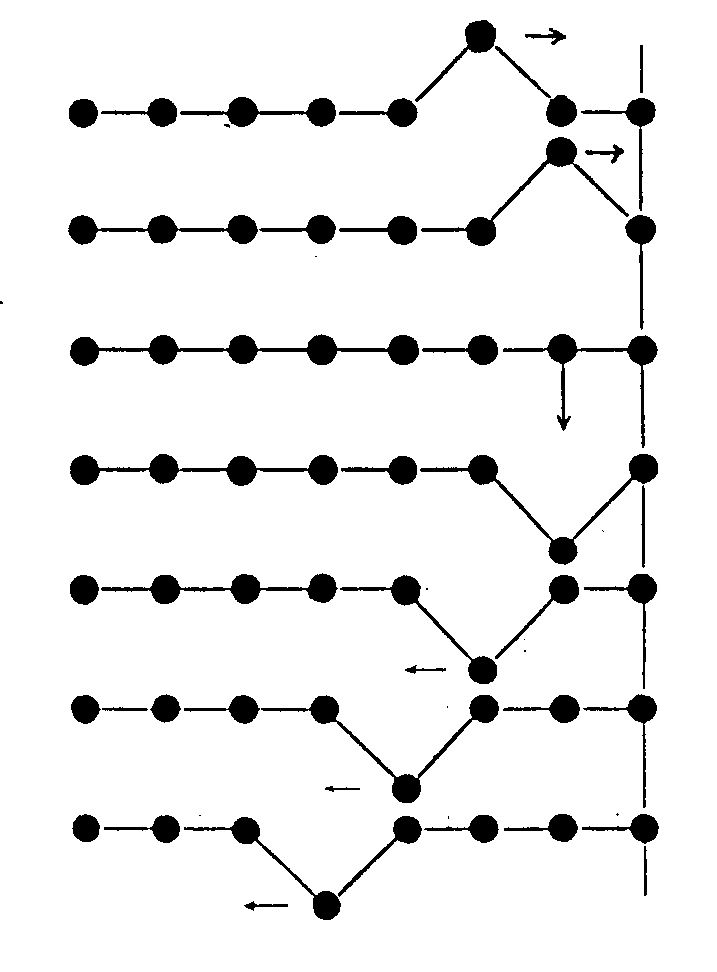Abb. 3: Reflexion am festen Ende: Die Pendelkugel am Ende wird festgehalten. Eine nach links laufende Welle entsteht aus einer vorher nach rechts laufenden Welle. An einem Endpunkt mit Reflexion am festen Ende befindet sich stets ein Knoten. An einem Endpunkt mit Reflexion am losen Ende kann die dort vorhandene Pendelkugel weitgehend frei auf und ab schwingen. Dort befindet sich ein Bauch mit maximaler Bewegung.

Wenn an beiden Endpunkten eine Reflexion am festen Ende stattfindet, befindet sich an beiden Enden der Pendelkette ein Knoten. Das lässt sich nur mit stehenden Wellen bestimmter Wellenlängen erfüllen. Ein Verfahren, mit dem man solche Wellenlängen ermitteln kann, ist das "Einpassen von halben Wellenlängen". In die Länge ℓ der Pendelkette passt nur ein ganzzahliges Vielfaches von halben Wellenlängen, und du erhältst ℓ = n·λ/2 (n = 1, 2, 3, ... ).

Wenn an beiden Endpunkten eine Reflexion am losen Ende stattfindet, befindet sich an beiden Enden der Pendelkette ein Bauch. Das "Einpassen von halben Wellenlängen" führt zum gleichen Ergebnis.

Wenn an den Endpunkten unterschiedliche Reflexionen stattfinden, muss du noch eine Viertelwellenlänge ergänzen:

ℓ = λ/4 + n·λ/2 (n = 0, 1, 2, 3, ... ).

(2) Die Situation lässt sich auch mathematisch beschreiben:

Eine ebene Welle laufe in positive x-Richtung (z.B. nach rechts). Bei einer mechanischen Welle gilt dann für die Auslenkung y₁:

        y₁ = A·sin(k·x-𝜔·t)

Die einzelnen Begriffe sind unten erklärt. Dass diese Welle in positive x-Richtung läuft, siehst du, wenn du einen Punkt mit der festen Phase k·x-𝜔·t betrachtest, z.B. k·x-𝜔·t = 0. Wenn du nach x auflöst, erhältst du x = t·𝜔/k = c·t. Mit wachsender Zeit t wird demnach die Koordinate x dieses Punktes immer größer.

Ganz entsprechend wird durch

eine in negative x-Richtung (nach links) laufende Welle beschrieben.

Wenn du beide Wellen überlagerst (addierst), erhältst du:

        y = y₁ + y₂ = A·{sin(k·x-𝜔·t) + sin(k·x+𝜔·t)}

Mit dem Additionstheorem der Trigonometrie

        sin(a) + sin(b) = 2 sin[(a+b)/2] cos[(a-b)/2]

findest du

        y = 2·A·sin[k·x]·cos[𝜔·t]

Du siehst, die Ortsabhängigkeit und die Zeitabhängigkeit sind getrennt. Der Sinus enthält die gesamte Ortsabhängigkeit, der Cosinus die gesamte Zeitabhängigkeit. An einem festen Ort x (sin[k·x] konstant) variiert y im Laufe der Zeit t zwischen 2·A·sin(k·x) und -2·A·sin(k·x). An Stellen mit k·x = n·𝜋 (n = 0, 1, 2, ... ) ist y stets 0, weil dort der  Sinus verschwindet. Diese Punkte werden Knoten genannt. Zwischen zwei Knoten dagegen liegt ein Bauch. Dort schwankt y im Laufe der Zeit t maximal zwischen -2·A und + 2·A.

t ist die laufende Zeit, x ein Ort längs der Ausbreitungsrichtung. 𝜔 ist die Kreisfrequenz 𝜔 = 2·π·f, f = 1/T die Frequenz. Die Bezeichnung Kreisfrequenz weist darauf hin, dass 𝜔 und f bis auf den Faktor 2·π identisch sind. Es gilt auch 𝜔 = 2·π/T, wobei T = 1/f die Schwingungsdauer ist. k = 2·π/λ  ist die so genannte Wellenzahl. Mit der Ausbreitungsgeschwindigkeit c gilt λ = c/f.