Beim Wurf wird einem Körper eine Anfangsgeschwindigkeit v0
erteilt. In der Folge wird der Körper durch die Gewichtskraft FG
beschleunigt. So sind also verschiedene Richtungen zu betrachten:
- die Richtung der Gewichtskraft FG senkrecht nach
unten,
- die Richtung des Beschleunigungsvektors a, gleichgerichtet
mit der Gewichtskraft FG ,
- die Richtung des Geschwindigkeitsvektors v, die sich auf
Grund der Anfangsgeschwindigkeit v0 und der
Beschleunigung a im Laufe der Zeit ergibt,
- die Richtung des Ortsvektors x.
Je nach der Richtung der Anfangsgeschwindigkeit v0
unterscheidet man zwischen senkrechtem/vertikalem, horizontalem und
schiefen Wurf.
Beim senkrechten Wurf ist die Anfangsgeschwindigkeit parallel
zur Gewichtskraft (nach unten) oder antiparallel (nach oben) gerichtet.
Es handelt sich um eine lineare Bewegung. Von allen Vektoren benötigt
man dann nur eine einzige Koordinate.
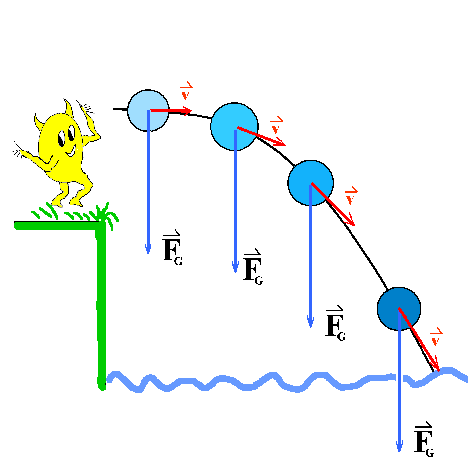 |
Hier wird ein Stein von den Klippen ins Meer
geworfen (horizontaler Wurf).
Die jeweilige Bewegungsrichtung ist durch die
roten Geschwindigkeitspfeile angedeutet. Die Kraft FG,
die Gewichtskraft, hat dabei aber immer die gleiche Richtung
senkrecht nach unten. Sie bewirkt eine Richtungsänderung und
eine Zunahme des Betrags der Geschwindigkeit, also eine
Beschleunigung a.
Beschleunigungsvektor a und
Kraftvektor FG sind immer gleich
gerichtet.
Zu Beginn des Wurfs ist der
Geschwindigkeitsvektor v gleich der
Anfangsgeschwindigkeit v0. Durch a
wird der Geschwindigkeitsvektor v allmählich nach
unten gedreht.
|
Beim schiefen Wurf schließt die
Anfangsgeschwindigkeit mit der Horizontalen einen beliebigen Winkel
ein.
Wenn eine Reibungskraft vernachlässigt werden kann, wie
Galilei schon vorgeschlagen hatte, handelt es sich um eine
gleichmäßig beschleunigte Bewegung, für die gilt:
| (1) x = x0 +
v0·Δt + 1/2 ·a· Δt2
(2) v = v0
+ a·Δt
(3) a = FG
/ m = g
|
g ist der Vektor der Fallbeschleunigung senkrecht
nach unten; die Beschleunigung a ist wie die Kraft konstant.
Die Masse m fällt dabei vollständig heraus: der Wurf ist dann
unabhängig von der Masse; insbesondere ist auch die Fallzeit aus einer
bestimmten Höhe unabhängig von der Masse m. Insbesondere beim
horizontalen wie beim schiefen Wurf kann es sinnvoll sein, die
Vektorgleichungen in Koordinatengleichungen zu zerlegen.
(Da es sinnvoll ist, das Zeitintervall Δt mit
dem Start zur Zeit 0 beginnen zu lassen, kann man statt Δt auch t
schreiben.)
Alle Würfe lassen sich auffassen als die Überlagerung
eines freien Fall mit einer gleichförmigen Bewegung mit der
Anfangsgeschwindigkeit v0. Die Zeitdauer des Wurfs
nennen wir hier "Flugdauer".
Daraus ergeben sich Folgerungen:
1. Beim horizontalen Wurf ist die Flugdauer
gleich der Fallzeit. Bereits beim Ablösen von der werfenden Hand
beginnt der Fall.
2. Beim waagrechten oder schrägen Wurf gilt:
| "Der Körper fliegt mit der horizontalen
Anfangsgeschwindigkeit so weit horizontal, wie er in der
Flugdauer kommt." |
3. Beim senkrechten Wurf nach oben:
| "Der Körper steigt soweit nach oben, bis die
anfängliche kinetische Energie aufgebraucht ist." |
Die anfängliche kinetische Energie ist dann ganz in
Lageenergie umgewandelt.
4. Beim senkrechten Wurf nach oben und beim schrägen
Wurf gilt:
| Um beim Fall vom Umkehrpunkt aus auf Starthöhe zu
kommen, wird eine Fallzeit t1 benötigt, die gleiche
Zeit um von der Starthöhe dorthin zu kommen. Vom Umkehrpunkt aus
fällt der Körper bis zum Zielniveau; dafür wird eine Fallzeit t2
benötigt. Insgesamt beträgt die Flugdauer t1 + t2. |
.
Der Freie Fall kann als senkrechter Wurf mit
v0 = 0 aufgefasst werden. Die
Koordinatengleichungen lauten dann (Koordinatenursprung im Startpunkt,
also x0 = 0; positive Koordinatenrichtung nach unten):
(1) x = 1/2 ·g· Δt2
(2) v = g·Δt
(3) a = FG / m = g
Aristoteles hatte dagegen einen anderen
Grenzfall untersucht, nämlich dem eines reibungsdominierten Falls. Für
ihn hatte er Recht!
(September 2013)
