|
Gegendarstellung zum
Wikipedia-Artikel "Elektromagnetische Induktion"
Spannung und Ringspannung -
eine Analyse
vor allem im Zusammenhang mit
der Induktion
|
Die Ringspannung (Umlaufspannung) im Unterschied zur gewöhnlichen
Spannung ist ein wichtiger Begriff im Zusammenhang mit der elektromagnetischen
Induktion. Eine weitere - weniger bedeutsame - Anwendung findet er
im Zusammenhang mit einem Gleichstromkreis mit einer Batterie. Es werden
hier einige Dinge richtig gestellt, die m.E. im Wikipedia-Artikel
Elektromagnetische Induktion (in der Version von Sept. 2012)
nicht korrekt dargestellt sind. Einen Vorschlag, wie diese Erkenntnisse in
den Physik-Unterricht der Schule einfließen könnten, finden Sie hier
oder hier.
1. Spannung in einem Potenzialfeld
In einem Kondensator herrsche ein homogenes elektrisches Feld, gerichtet
von der positiven zur negativen Platte. Bei der Verschiebung einer
positiven Probeladung (q > 0) in Richtung von der negativen zur
positiven Platte muss (positive) Verschiebungsarbeit aufgewendet werden.
Diese ist nur abhängig von den beiden Abständen von einer der Platten,
nicht vom Weg, auf dem die Verschiebung erfolgt. Wenn das - wie hier - der
Fall ist, spricht man allgemein von einem Potenzialfeld.
Die Verschiebung soll ohne Zufuhr von kinetischer Energie erfolgen, d.h.
sie soll so geschehen, dass die Ladung (quasi) nicht beschleunigt wird.
Das ist dann der Fall, wenn die externe verschiebende Kraft Fext
entgegengesetzt gleich zur Kraft F ist, die das elektrische Feld
auf die Probeladung q ausübt (nur ein Überschuss könnte auch
beschleunigen). Es gilt dann für die Verschiebungsarbeit der Ladung von
einem Punkt 1 zu einem Punkt 2, deren Abstand von den Platten sich um eine
Strecke d unterscheidet (wenn z.B. die Probeladung entgegengesetzt zur
elektrischen Feldstärke E verschoben wird):
W12 = ∫ von 1 bis 2 (Fext·ds) = - ∫
von 1 bis 2 (F·ds) = - q · ∫ von 1 bis 2 (E·ds)
= q·E·d > 0
.
Für die Definition der Spannung gibt es zwei unterschiedliche
Konventionen. Zur Erzielung einer konsistenten Formulierung wird hier die
meist übliche Konvention 2 angewandt. Der Leser sollte auf die
Unterscheidung nicht allzuviel Energie aufwenden.
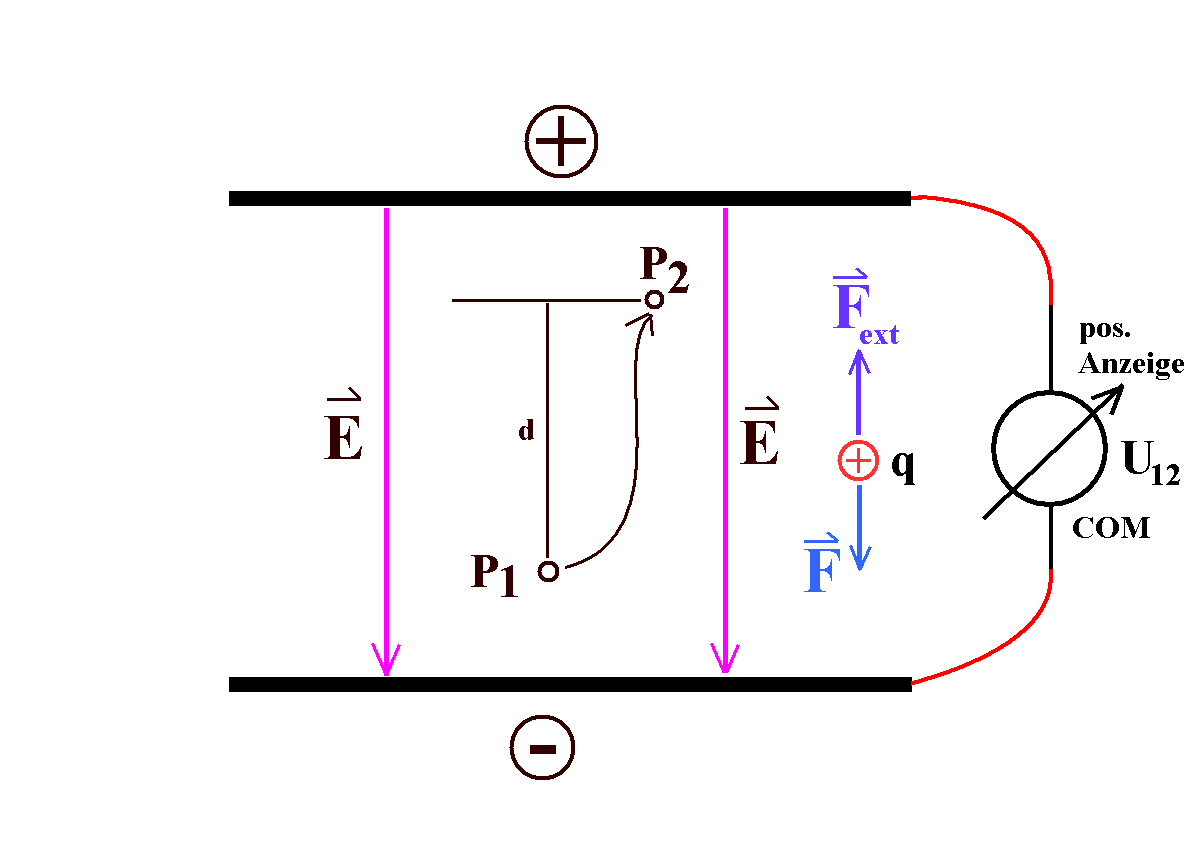 |
Abb. 1:
Nach Konvention 1 ist die Spannung U12 am
positiven Pol im Vergleich zum negativen Pol positiv! Eine äußere
Kraft muss für die Verschiebung von 1 nach 2 positive
Arbeit verrichten.
U12 nach Konvention 1 wird von einem
Spannungsmesser richtig angezeigt, wenn sein Massepol (COM) mit
dem Minuspol verbunden wird.
|
Konvention 1: Definiert man als Spannung am Punkt 2 in
Vergleich zu Punkt 1 (also U12) die für die Verschiebung
benötigte Verschiebungsarbeit pro Ladungseinheit, also
U12 = W12/q = E·d
erhält man eine positive Spannung, wenn der Endpunkt der Verschiebung
näher an der positiven Platte liegt.
Verschiebt man in gleicher Weise von irgendeinem Punkt x0 zu
einem Punkt x, dann muss man die Arbeit W0x = q·E·(x - x0)
aufwenden. Definiert man ein Potenzial Φ (Fi) als Verschiebungsarbeit pro
Ladungsmenge, also Φ(x) = W0x/q = E·(x - x0), so
entspricht die Spannung U12 der Potenzialdifferenz Φ(x2)
- Φ(x1): Wenn am Zielpunkt x2 ein höheres Potential
herrscht als am Ausgangspunkt x1, ist die Spannung am Zielpunkt
im Vergleich zum Ausgangspunkt positiv.
| Spannung als Verschiebungsarbeit
pro Ladungsmenge gilt allgemein, der Zusammenhang mit
der Potenzialdifferenz nur, wenn die Verschiebung wegunabhängig
ist, wenn also ein Potenzialfeld vorliegt. |
Konvention 2: Es ist meistens üblich, das Vorzeichen der
Spannung umgekehrt zu wählen, also U12 = Φ(1) - Φ(2). Dann ist
die Spannung am Punkt 2 im Vergleich zum Punkt 1 die Arbeit pro
Ladungsmenge, die das Feld verrichtet bei einer Verschiebung von
1 nach 2. Im elektrischen Feld gilt dann also U12 =∫ von 1 bis
2 (E·ds) .
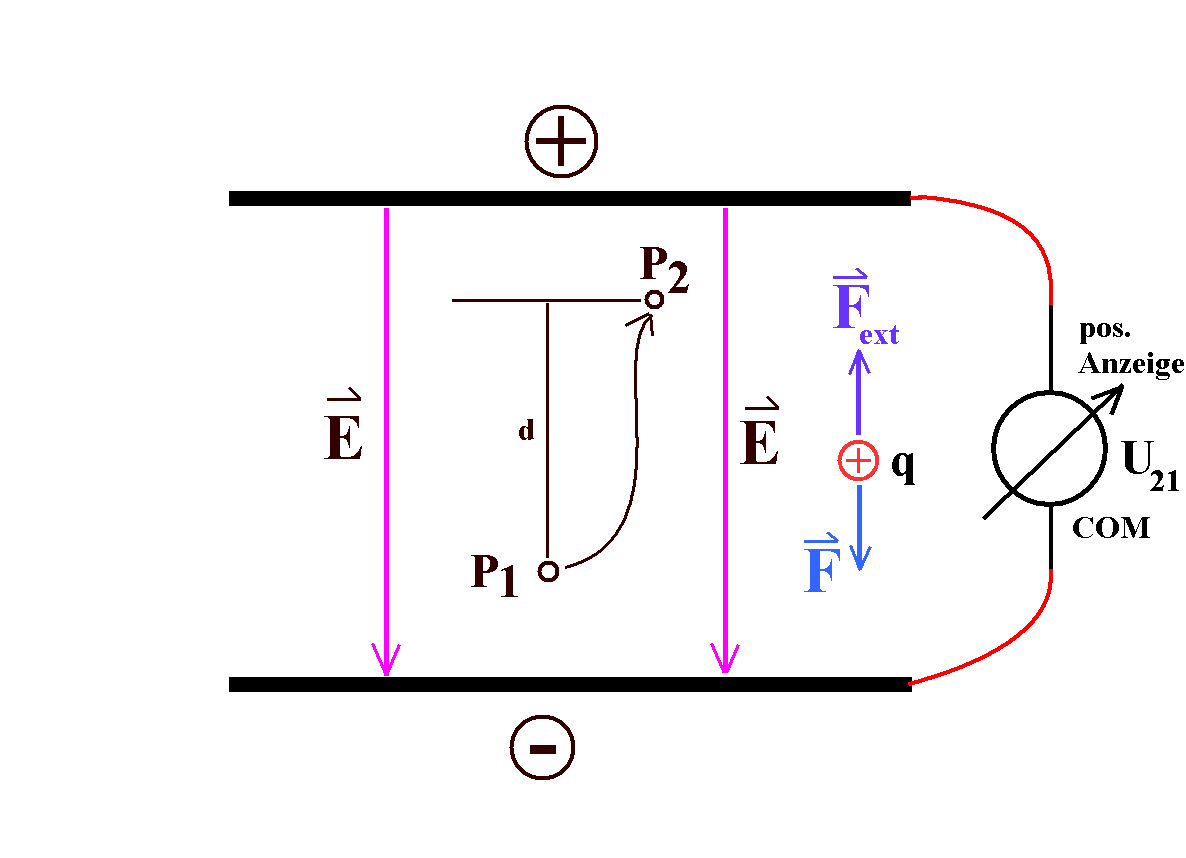 |
Abb. 2:
Nach Konvention 2 ist die Spannung U12 am
positiven Pol im Vergleich zum negativen Pol negativ! Das Feld
verrichtet negative Arbeit, d.h. es muss von außen
positive Arbeit zugeführt werden, wenn es eine positive
Probeladung von der negativen zur positiven Platte verschiebt.
Die Spannung U21 am negativen Pol ist dann im
Vergleich zum positiven Pol positiv.
U21 nach Konvention 2 wird von einem
Spannungsmesser richtig angezeigt, wenn sein Massepol (COM) mit
dem Minuspol verbunden wird.
|
Wir wollen im Folgenden gemäß Konvention 2 vorgehen. In einem
Plattenkondensator ist das elektrische Feld von + nach - gerichtet. Legt
man den Potenzialnullpunkt auf die negative Platte, hat die positive
Platte positives Potenzial (eine äußere Kraft muss positive Arbeit
verrichten, um eine positive Probeladung von der negativen zur positiven
Platte zu verschieben. Dagegen hat die negative Platte im Vergleich zur
positiven Platte positive Spannung (im Sinne der Konvention 2), weil das Feld
für die Verschiebung einer positiven Probeladung von der positiven zur
negativen Platte positive Arbeit verrichtet, also Arbeit/Energie nach
außen abgibt.
Welche Konvention tatsächlich verwendet wird, ist weitgehend belanglos.
Man sollte nur konsequent bei einer bleiben. In der Praxis misst man
Spannungen mit dem Voltmeter. Erhält man einen positiven Ausschlag, weiß
man auf jeden Fall, dass der Masse-Anschluss (COM) mit dem negativen Pol
der Spannungsquelle verbunden ist, der andere mit dem positiven. Dass man
nach der einen Konvention U12 gemessen hat, nach der anderen U21,
ist recht belanglos. Das ist wohl der Grund, weshalb in den meisten
Büchern zwar beim Potenzial auf die Reihenfolge geachtet wird, dass es
aber bei der Spannung meistens nur heißt "Spannung zwischen ... ".
.
2. Ringspannung
Wenn kein Potenzialfeld vorliegt, wenn also die Spannung
wegabhängig ist, gibt es Situationen, wo eine Verschiebungsarbeit
aufgewendet werden muss für eine Verschiebung von einem Punkt auf einem
Umweg zum gleichen Punkt zurück. Eine solche Situation liegt bei der
Induktion vor. Es ist naheliegend, hier eine Ringspannung (oder
Umlaufspannung) analog zu definieren durch die Verschiebungsarbeit W für
einen vollen Umlauf:
URing = W/q = ∫0 (F·ds) / q .
Dabei ist F die Kraft, die das elektromagnetische Feld auf die
Ladung ausübt ( ∫0 : Ringintegral über einen geschlossenen
Weg).
Wenn nur ein elektrisches Feld vorliegt, folgt daraus sogar
URing = q · ∫0 (E·ds) / q = ∫0
(E·ds)
Offenbar ändert sich das Vorzeichen der Ringspannung mit dem
Umlaufssinn. Mit der Wahl des Umlaufssinns ist also eine gewisse Willkür
verbunden. Wie die gewöhnliche Spannung hat die Ringspannung die Einheit 1
V.
Wenn diese Ringspannung von 0 verschieden ist, spricht man von einem
elektrischen Wirbelfeld E. In einem Potenzialfeld ist die
Ringspannung wegen der Wegunabhängigkeit 0.
.
3. Ringspannung bei der Induktion
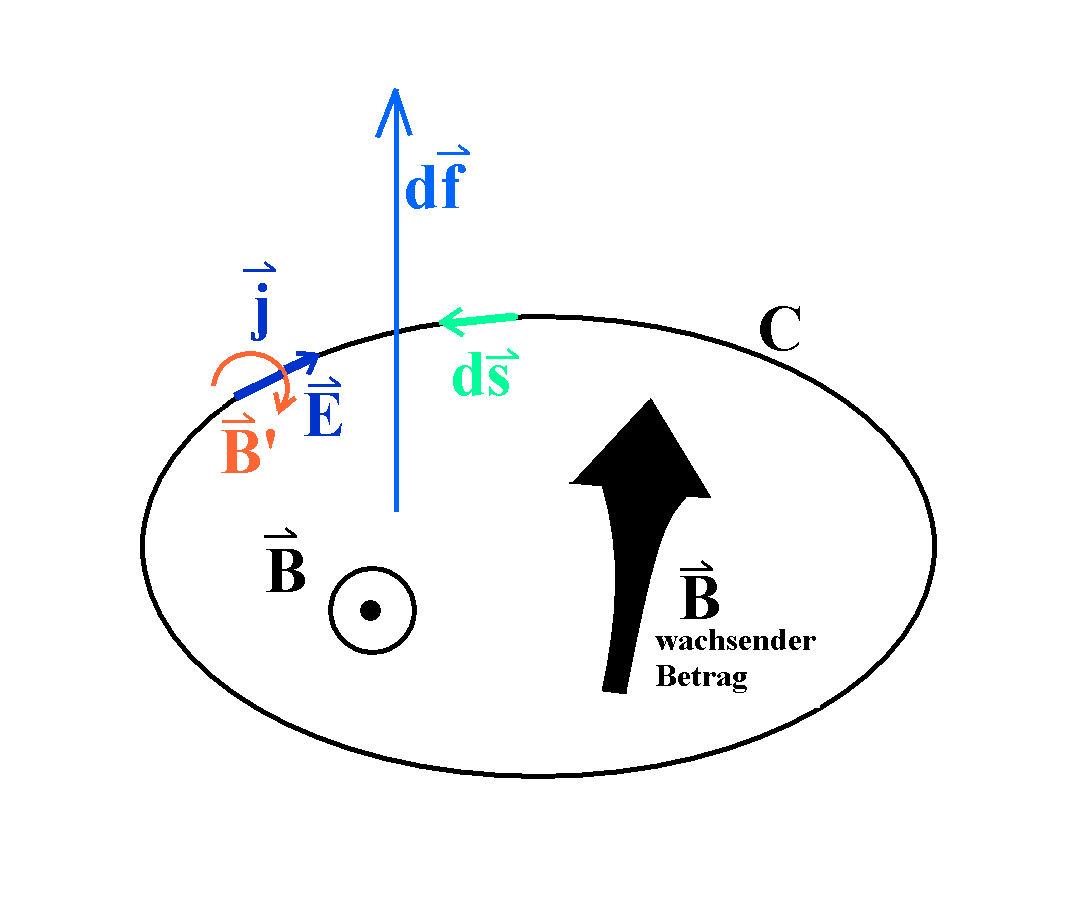 |
Abb. 3:
Orientierungen, die im Induktionsgesetz verwendet werden
Die Richtungen des Linienelements ds und des
Flächenelements df ergeben sich aus folgender Regel:
Wenn der Daumen der rechten Faust in Richtung des
Flächenelements df zeigt, dann zeigen die Fingerspitzen
die Orientierung des Linienelements ds an.
Geschlossener Stromkreis, zunehmendes Magnetfeld mit
Orientierung nach Zeichnung: Mit der Lenz'schen Regel überlegt
man sich die Richtung des Stroms (hier des Stromdichtevektors j).
Der Strom j muss so orientiert sein, dass das von ihm
erzeugte Magnetfeld B' den Zuwachs von B zu
verhindern versucht. Wegen des Ohm'schen Gesetzes j = σ
· E ist der Vektor des durch die Induktion entstandenen
elektrischen Feldes E gleichgerichtet zu j; σ
= sigma = Leitfähigkeit.
|
Der Wikipedia-Artikel "Elektromagnetische Induktion" führt eine
"Integralform I" des Induktionsgesetzes an. Sie lautet:
∫0 (E·ds) = - ∫ ∂B/∂t · df (∂
partielle Ableitung) für irgendeine Kurve C, die eine Fläche A
einschließt, welche vom Magnetfeld B durchsetzt wird. df
und ds sind nach der Rechten-Faust-Regel orientiert, d.h., wenn
der rechte Daumen in Richtung eines Flächenelements df zeigt,
zeigen die Fingerspitzen die Richtung der Linienelemente ds an.
Für den Fall, dass keine Bewegung der Kurve C im B-Feld
stattfindet (d.h. keine Bewegung in einem BZS, in dem das Magnetfeld B
gemessen wird), können wir jetzt die Ringspannung leicht berechnen: Durch
die äußere Kraft muss bei der Verschiebung längs der Kurve C nur Arbeit
gegen das elektrische Feld verrichtet werden. Es gilt dann:
URing = ∫0 (E·ds) = - ∫ ( ∂B/∂t
· df ) (partielle Ableitung ∂B/∂t )
In diesem Fall ist die Ringspannung URing gleich der
negativen Zeitableitung des magnetischen Flusses Φ = ∫ ( B ·
df ), der die Kurve C durchsetzt
.
4. Wie kann die Ringspannung gemessen werden?
a) In einem geschlossenen Stromkreis mit einem Gesamtwiderstand
R > 0 ist die Folge der Ringspannung ein Stromfluss in Richtung
von E (für die Stromdichte j gilt häufig nach dem
Ohm'schen Gesetz j = σ ·E) längs der Kurve C, wenn C also
mit einem Leiterring belegt ist. Es gilt also
URing = ∫0 (E·ds) = ∫0 (j·ds)
/ σ = - I·R (zumindest bei einem homogenen Leiter
überall gleichen Querschnitts und gleicher Leitfähigkeit σ ist das
evident; Minuszeichen, da j und ds entgegengesetzt)
|
Die
Ringspannung wird also gemessen durch die (Ring-)Stromstärke im
geschlossenen Stromkreis längs der mit dem Leiter belegten Kurve
C. (Messmöglichkeit
a)
|
Dann gilt also - I·R = - ∫ ( ∂B/∂t · df ) = - dΦ/dt
Ein wachsender magnetischer Fluss Φ führt dann gemäß Abb. 3 zu
einem positiven Strom I, d.h. zu einem Strom entgegengesetzt zu ds (entgegengesetzte
Richtungen schon in - I·R berücksichtigt).
.
b) Jetzt sei der Leiterring unterbrochen mit einer schmalen
Lücke mit den Klemmen 1 und 2. Das elektrische Feld E verschiebt
nun mit der Kraft F = q·E Ladungen q parallel oder
antiparallel zu E.
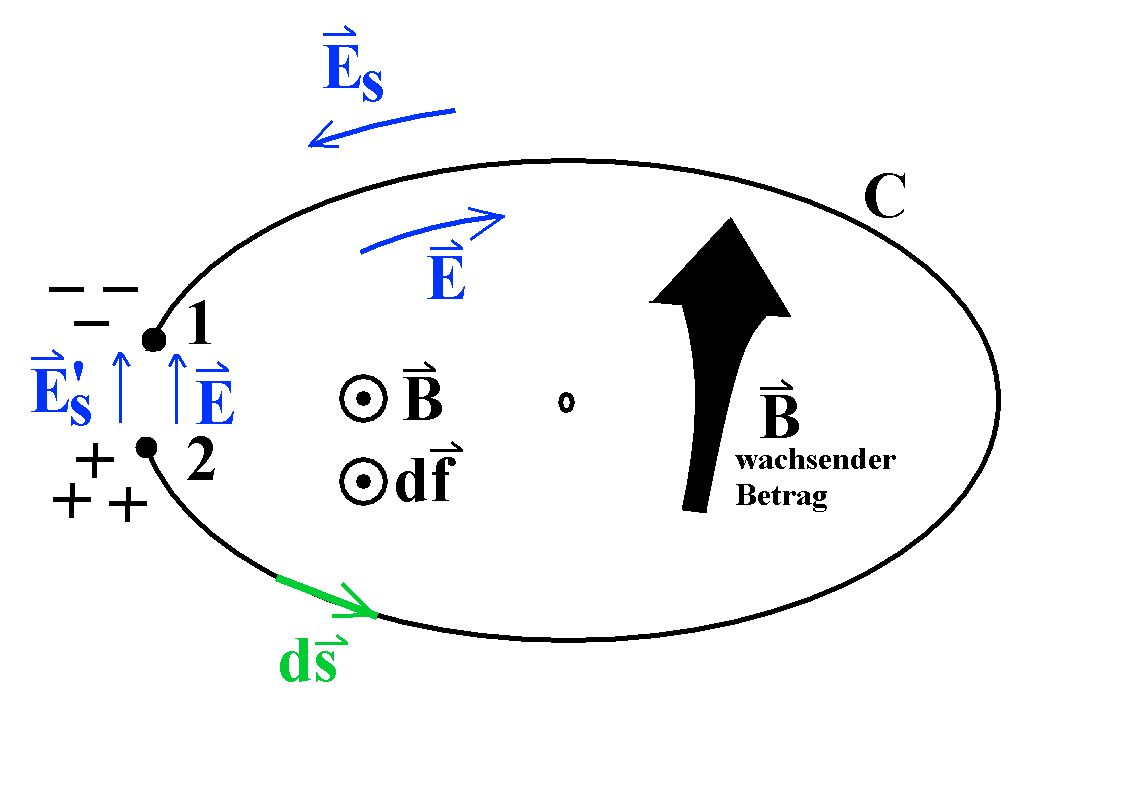 |
Abb. 4:
Die negativen (Leitungs-)Elektronen werden antiparallel zu E
verschoben und stauen sich an der Lücke. Dadurch entsteht ein
zusätzliches elektrisches Feld ES, das auf
die Elektronen ebenfalls eine Kraft ausübt. Wenn ein stationärer
Zustand erreicht ist, gilt Kräftegleichgewicht und damit E
= - ES im Leiter. Dann ist das Innere des
Leiters feld- und kräftefrei; zur Verschiebung einer Probeladung
im Leiterinneren muss keine Arbeit aufgewendet werden. ES
ist, da von Ladungen erzeugt, ein Potenzialfeld. Außerhalb des
Leiters, in der Lücke, sind aber E und Es
gleich gerichtet.
Das Induktionsgesetz gilt unter den oben genannten
Voraussetzungen sowohl für das Feld E allein, als auch
für das Gesamtfeld, das im Leiterinneren verschwindet, weil das
Potenzialfeld ES keinen Beitrag zum
Ringintegral leisten kann.
|
Für die Ringspannung gilt: URing = ∫0 (E·ds)
= ∫0 (E·ds) + ∫0 (ES·ds);
weil ES ein Potenzialfeld ist, können wir
den zweiten verschwindenden Term ergänzen ( ∫0 :
Ringintegral über einen geschlossenen Weg). Wir wollen die Ringintegrale
aufspalten und neu ordnen, wobei wir uns an die durch ds
vorgegebene Umlaufsrichtung halten:
URing = ∫ von 2 bis 1 (E·ds) + ∫ von 2 bis 1 (ES·ds)
+ ∫ von 1 bis 2 (E·ds) + ∫ von 1 bis 2 (E'S.ds)
=
∫ von 1 bis 2 (E·ds)
+ ∫ von 1 bis 2 (ES·ds) + ∫ von 2 bis 1 ((E+ ES)·ds)
Der dritte Term verschwindet im Leiter. Der erste Term kann
vernachlässigt werden, wenn die Lücke schmal ist. Schmale Lücke hat aber
großes E'S in der Lücke zur Folge. Deswegen gilt in
guter Näherung für eine schmale Lücke:
URing = ∫ von 1 bis 2 (ES·ds).
Das ist aber gerade die gewöhnliche Spannung U12 = - U21
zwischen beiden Klemmen infolge des sekundär entstandenen Potenzialfelds ES.
Also:
|
Als zweite Möglichkeit für die Messung der
Ringspannung steht uns also die Überführung in eine gewöhnliche
Spannung im unterbrochenen Stromkreis zur Verfügung, wenn die
Klemmen durch eine schmale Lücke getrennt
sind. (Messmöglichkeit
b)
|
Es gibt Situationen, wo man auf die Einschränkung "schmale Lücke"
verzichten kann.
.
5. Ringspannung und Spannung bei der Induktion
Dann haben wir also für diesen Fall der Induktion: (URing
= - ∫ ( ∂B/∂t · df ) = - dΦ/dt )
In dieser Form wird das Induktionsgesetz in der Regel in der Schule
gelehrt.
( Hätte man für die Definition der Ringspannung den umgekehrte
Durchlaufssinn gewählt, hätte man gefunden:
URing = ∫ von 1 bis 2 (E·ds) + ∫ von 1 bis 2 (ES·ds)
+ ∫ von 2 bis 1 (E·ds) + ∫ von 2 bis 1 (E'S·ds)
=
= ∫ von 2 bis 1 (E·ds)
+ ∫ von 2 bis 1 (ES·ds) + ∫ von 1 bis 2 ((E +
ES)·ds)
= ∫ von 2 bis 1 (ES·ds)
URing = U21 = - U12 = - dΦ/dt, also
umgekehrtes Vorzeichen. )
.
6. Spannung und Ringspannung bei der Induktion im
zeitlich konstanten Magnetfeld
Wenn jetzt aber das Magnetfeld zeitlich konstant ist, dann
würde das Induktionsgesetz in der angegebenen Form (Integralform I nach
Wikipedia) sagen, dass E im betrachteten Bezugssystem kein
Wirbelfeld ist, weil das Ringintegral über E verschwindet. Gibt es
in diesem Fall also keine Ringspannung? Aber wir wissen doch, dass
Induktion entstehen könnte, wenn sich Teile der geschlossenen
Leiterschleife im (homogenen oder inhomogenen) Magnetfeld bewegen. Auch
ein Beobachter, der sich längs der geschlossenen Leiterschleife bewegt,
würde in seinem jeweiligen Bezugssystem ein elektrisches Wirbelfeld und
damit eine von 0 verschiedene Ringspannung feststellen. Häufig wird in
einem solchen Fall die Lorentz-Kraft q v x B
von außen ins Spiel gebracht. Sie ist in der Integralform I nicht
enthalten. Der Wikipedia-Artikel macht das, indem er das Ohm'sche Gesetz
bemüht (Induktion eine Folge des Ohm'schen Gesetzes?).
Überlegen wir uns das vom Anfang an noch einmal :
URing = W/q = ∫0 (F·ds) / q , wobei
F die Feldkraft ist, gegen die die äußere Kraft bei der
Verschiebung auf einer geschlossenen Kurve C Arbeit verrichten muss. Ein
rein elektrischer Anteil könnte nach Integralform I nichts zum
Ringintegral ∫0 beitragen, höchstens ein Anteil durch die
Lorentz-Kraft, dort, wo die Lorentz-Kraft von 0 verschieden ist. Dann
haben wir:
URing = ∫0 (F·ds) / q = ∫0
(( v x B ) · ds)
.
Untersuchen wir das in einem Beispiel:
Auf den Schenkeln eines U-förmigen Leiters gleitet eine Leiterbrücke mit
gutem Kontakt. Senkrecht zur so aufgespannten Rechtecksfläche wirke ein
Magnetfeld B. Der Widerstand des geschlossenen rechteckigen
Leiterkreises sei größer als 0. Beim Gleiten ändert sich der
eingeschlossene magnetische Fluss. Wir erwarten also Induktion, einen
Ringstrom I, und, angetrieben durch die Lorentzkraft, eine Ringspannung.
Die Orientierung seien entsprechend der Zeichnungen (Abb. 5, 6).
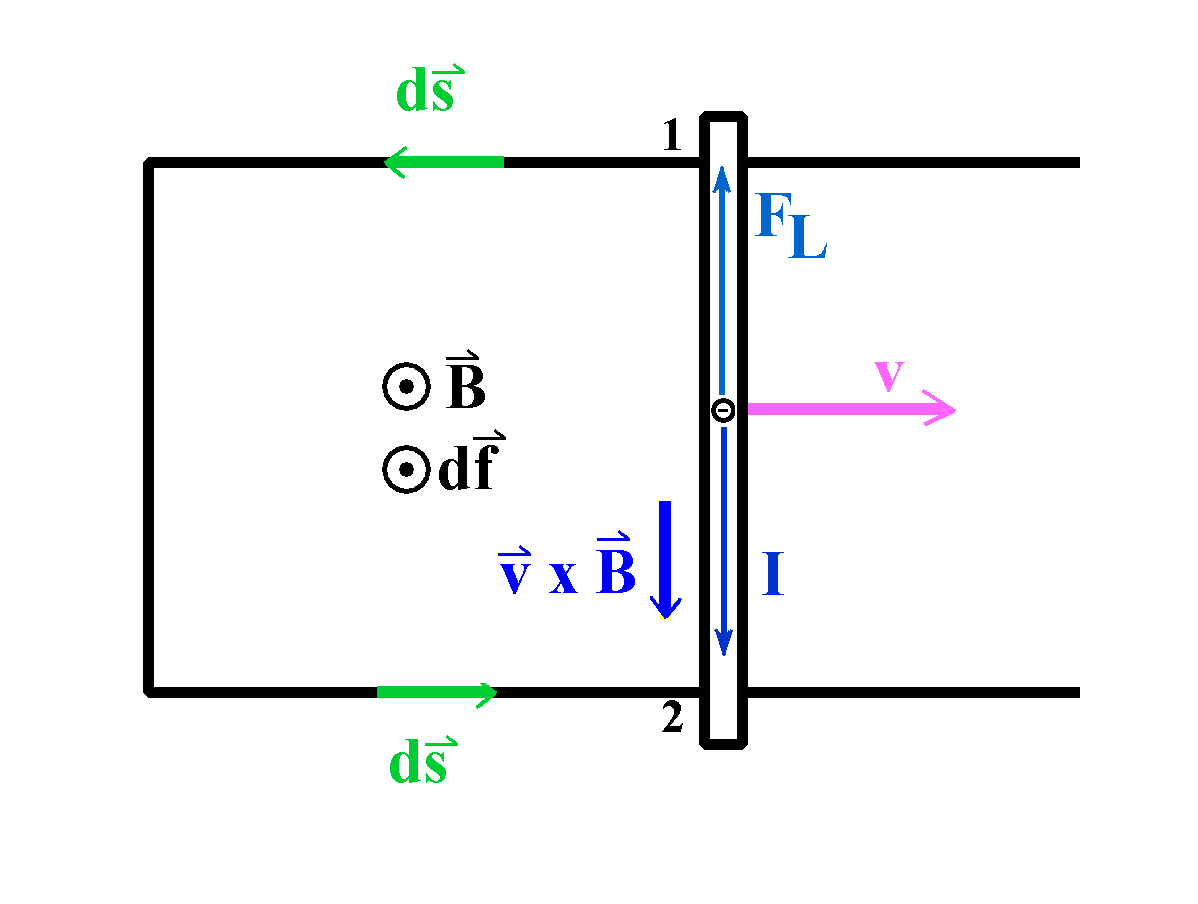 |
Abb. 5:
Geschlossener Leiterkreis:
Weil v x B überall verschwindet, außer in der
bewegten Leiterbrücke, reduziert sich die Ringspannung hier auf
ein gewöhnliches Integral:
URing = ∫ von 2 nach 1 (v x B · ds)
v x B ist längs des I-Pfeils (in der Zeichnung nach
unten) gerichtet, also entgegengesetzt zu ds. Es ergibt
sich also
URing = - B·v·L,
wenn L die Länge der Leiterbrücke ist.
Das negative Vorzeichen besagt: Das elektromagnetische Feld
verrichtet negative Arbeit um eine positive Ladung in Richtung
v x B zu verschieben (also einen Strom I zu
erzeugen), benötigt also Energiezufuhr von außen für diesen
Induktionsvorgang. Es lässt sich begründen, dass dazu eine
äußere Kraft Fext in Richtung v
ausgeübt werden muss.
Mit der Flussregel geht es auch: Bei dieser Orientierung von B,
df und v nimmt der eingeschlossene
magnetische Fluss im Laufe der Zeit zu um B·v·L. Die
Ringspannung ist also URing = - dΦ/dt = - B·v·L
|
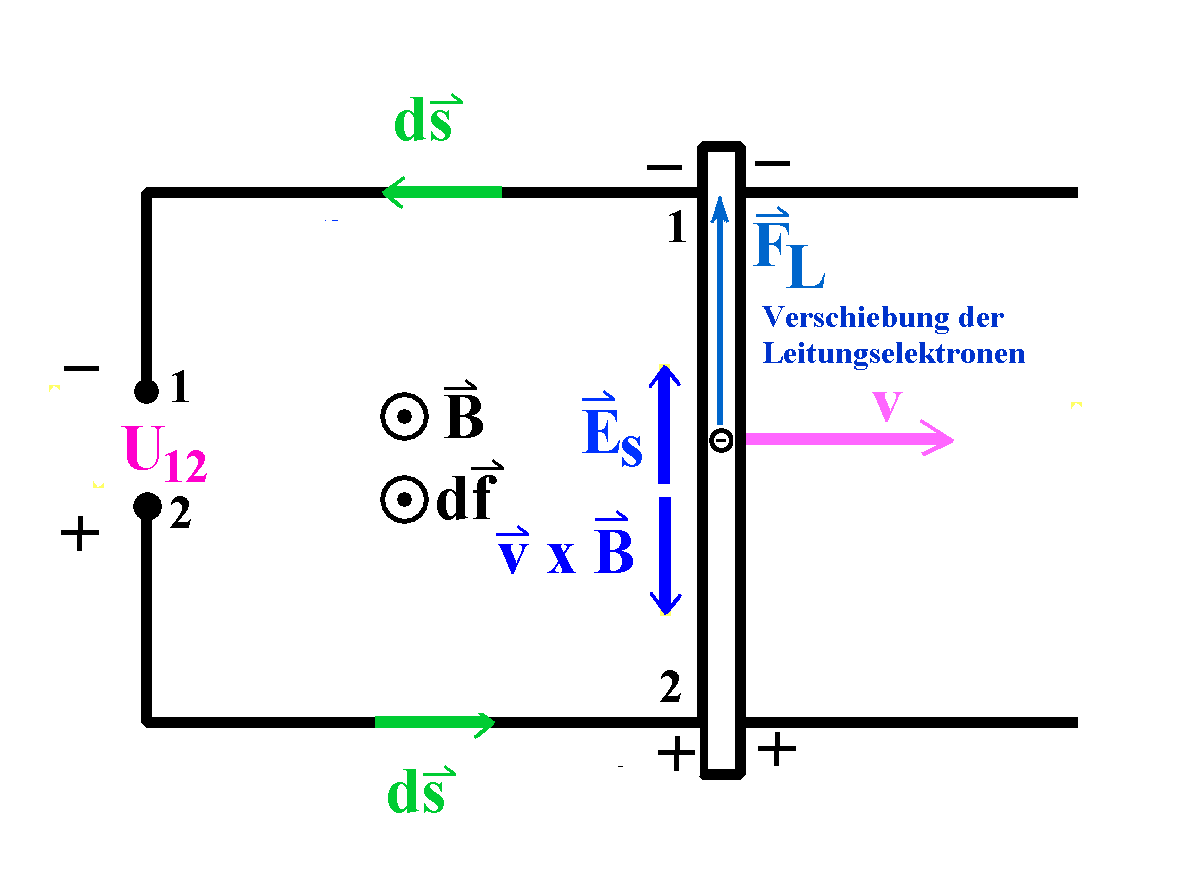 |
Abb. 6:
Unterbrochener Leiterkreis:
Die Berechnung der Ringspannung erfolgt identisch. Ein
anderer Weg geht so:
Durch die Verschiebung der Leitungselektronen bildet sich
wieder ein sekundäres statisches Feld ES aus.
v x B ist nur in der Leiterbrücke von 0 verschieden. Es
stellt sich ein stationärer Zustand ein, wenn auf die
Leitungselektronen in der Leiterbrücke Kräftegleichgewicht (KGG)
herrscht. Dann gilt also dort ES = - v
x B (in der Leiterbrücke von 2 nach 1 gerichtet). Da ES
in der Leiterbrücke konstant ist, gilt die Kondensatorformel: U12
= ES·L = - B·v·L . Das Minuszeichen kommt hier
herein, weil die Spannung vom negativen zum positiven Pol
gemessen wird.
Da es keine Spannungsabfälle gibt, ist auch die Spannung
zwischen den Klemmen (2 gegenüber 1) von gleicher Größe, und
zwar in dieser Situation negativ.
Für die Verschiebung einer zusätzlichen positiven Probeladung
vom negativen (1) zum positiven Ende (2) der Leiterbrücke
- entgegengesetzt gerichtet zu - v x B - muss das
elektromagnetische Feld negative Arbeit verrichten, d.h. es
benötigt Arbeit von außen.
Die Ringspannung im geschlossenen Leiterkreis und die
elementare Überlegung im offenen Leiterkreis führen zum gleichen
Ergebnis.
|
Obwohl das elektrische Feld E im Laborsystem (in dem der
U-förmige Leiter ruht) auf die bewegte Leiterbrücke beschränkt ist, gibt
es hier einen Ringstrom I und eine nicht verschwindende Ringspannung.
Deswegen heißt dieser Vorgang mit Recht ebenfalls Induktion.
(Abgesehen von einigen Komplikationen) liegt im System der Leiterbrücke
aber das elektrische Feld E' = v x B (in
nichtrelativistischer Näherung für v << Lichtgeschwindigkeit c) vor.
Es ist ein elektrisches Wirbelfeld (weil rot' E' ≠ 0) und führt
ebenfalls zur nicht verschwindenden Ringspannung, also: gleiches Ergebnis
in beiden Bezugssystemen.
Nirgendwo kommt hier eine Leitfähigkeit ins Spiel (natürlich sollten die
Leiter nicht aus einem Isolatormaterial bestehen). Nur, wenn man die
Ringspannung durch die Stromstärke I messen will, braucht man das Ohm'sche
Gesetz ( /URing/ = /I·R/).
(Wenn der Widerstand R verschwindet, z.B. bei Supraleitern, wird
im geschlossenen Leiterkreis nach der Lenz'schen Regel eine
Flussänderung vollständig unterdrückt (idealer Diamagnetismus). Zur
Berechnung der Stromstärke müssen dann statt des Ohm'schen Gesetzes die
London-Gleichungen herangezogen werden. Vgl. Industrom.html.
Die Folge ist z.B., dass in einem geschlossenen Leiterring die
Stromstärke proportional zum magnetischen Fluss ist und nicht zu seiner
Zeitableitung wie bei R > 0, also nach dem gewöhnlichen
Induktionsgesetz!)
.
7. Ringspannung bei der Induktion im allgemeinen Fall,
also, wenn eine Bewegung der Leiterschleife im inhomogenen und zeitlich
veränderlichen Magnetfeld erfolgt:
Das Feld übt eine Kraft F = q · ( E + v x B )
auf eine positive Probeladung q aus. Dementsprechend entsteht von beiden
Anteilen her ein nicht verschwindender Beitrag zur Ringspannung:
URing = ∫0 (( E + v x B )· ds)
= - dΦ/dt
Beide Anteile sind in der Integralform II des Wikipedia-Artikels von
vornherein vorhanden, ohne dass man die Lorentz-Kraft explizit noch einmal
berücksichtigen muss. Es kam dort implizit durch die Maxwell-Gleichung div
B = 0 herein.
Im Bezugssystem der bewegten Leiterbrücke ist E + v x B
in nichtrelativistischer Näherung gerade das dort herrschende elektrische
Feld E'. Dann gilt also
URing = ∫0 (E'· ds) = - dΦ/dt
und aus der Sicht des mitbewegten Beobachters liegt bei einer Änderung
des magnetischen Flusses ein elektrisches Wirbelfeld E' vor.
( Für praktische Rechnungen kommt es häufig auf die Spannungsvorzeichen
nicht an, auch, weil sie von Konventionen abhängig sind. Deswegen sollte
man auf sie nicht allzuviel Energie aufwenden. Hätte man Konvention (1)
für die Spannungsdefinition verwendet, hätte gegolten:
- URing = ∫0 (( E + v x B ) ·
ds) = - dΦ/dt , URing = U12
= dΦ/dt und URing = I · R . Das hätte einige
weitere Vorzeichenänderungen zur Folge gehabt. )
Hinweis: Bei der Interpretation der Lorentz-Kraft F = q
( E + v x B ) muss man Vorsicht walten lassen. Man könnte
sagen, dass sie bei der Induktion selbst dann in dieser Weise auf Ladungen
wirkt, wenn am Ort der Ladungen das Magnetfeld völlig abgeschirmt
oder auf eine andere Weise zu 0 gemacht wurde. Letzten Endes ist Induktion
eine Sache der Felder und nichtlokal. Vgl.: Was
ist elektromagnetische Induktion ?
.
.
8. Ringspannung und Spannung bei einem Gleichstromkreis
mit einer Batterie
Inwiefern bei einem geschlossenen Stromkreis mit einer Batterie ein
Potenzialfeld vorliegt, wird in Standard-Lehrbüchern diskutiert. Dort wird
auch gezeigt, dass ein reines Potenzialfeld nicht die Energie für einen
stationären Strom herbeischaffen kann. Die Überlegung ist eher
grundsätzlicher Art. Vgl. auch emk.html
.
.
9. Hier irrt der Wikipedia-Artikel
Es werden hier nur die wichtigsten Einwände formuliert (über weitere
habe ich mich schon früher geäußert):
1. Die differentielle Form und die Integralform I des Induktionsgesetzes
in der Formulierung des Wikipedia-Artikels sind m.E. nicht äquivalent zur
Integralform II . Wenn das Magnetfeld nicht zeitabhängig ist, enthalten
die differentielle Form und die Integralform I m.E. nicht die Induktion.
Es ist deshalb auch am elektrischen Feld E allein nicht erkennbar,
dass Induktion und eine von 0 verschiedene Ringspannung vorliegt. Der
Wikipedia-Artikel mogelt die Induktion nur nachträglich mit Hilfe des
Ohm'schen Gesetzes (bzw. der Lorentz-Kraft) für einen unterbrochenen
Leiter hinein, während in der Integralform II des Induktionsgesetzes alle
Varianten automatisch enthalten sind.
2. Es ist nicht erkennbar, wie der Wikipedia-Autor im Fall eines
zeitunabhängigen Magnetfelds bei einem geschlossenen Leiterkreis
eine Induktionsspannung (und damit einen Ringstrom) begründen möchte. Mit
der in diesem Artikel gezeigten Ringspannung ist das kein Problem.
3. Der Wikipedia-Artikel beruft sich immer wieder auf die Gültigkeit des
Ohm'schen Gesetzes. Er könnte im unterbrochenen Stromkreis - dort
setzt er es ein - bei gleichem Ergebnis auch mit dem Kräftegleichgewicht
infolge der Lorentz-Kraft argumentieren. Das wäre m.E. physikalisch
klarer. Vor allem aber wäre Induktion nicht an die Anwendbarkeit des
Ohm'schen Gesetzes gebunden. Es wäre ja wohl etwas merkwürdig, wenn das
allgemeine Induktionsgesetz von einer speziellen materialabhängigen
Gleichung wie dem Ohm'schen Gesetz abhinge.
4. Der Wikipedia-Artikel geht manchmal von der Behauptung aus, dass in
einem idealen Leiter kein elektrisches Feld möglich sei. Für den
Gleichgewichtsfall, im unterbrochenen Stromkreis bzw. in der Elektrostatik
gilt das sicher, dann sogar unabhängig von der Leitfähigkeit. Aber bei der
Induktion im geschlossenen Stromkreis liegt gerade die Situation vor, dass
das ringförmige elektrische Feld im Leiter den Strom antreibt
(auch bei der Leitfähigkeit σ = 0 ; siehe hier),
dass sich also der Gleichgewichtsfall nicht einstellt, solange Induktion
stattfindet. Der Wikipedia-Artikel zieht daraus falsche (teilweise sogar
widersprüchliche) Schlüsse bzgl. der Induktion in einem geschlossenen
idealen Leiter und bzgl. des Hering'schen Paradoxons. Die dortigen
Ausführungen stellen so nur einen Teil der Wahrheit dar.
.
10. Hinweise zur Definition einer Ringspannung
Backhaus und Braun (Physik und Didaktik in Schule und Hochschule, PhyDid
1/5 (2006) S. 45 - 53) diskutieren verschiedene experimentelle Folgen der
Ringspannung. Sie schlagen auch vor, unter Spannung so etwas Ähnliches wie
die Ringspannung zu verstehen, die in der theoretischen Physik üblich ist.
Darüberhinaus wird in diesem Artikel gezeigt, dass es Sinn macht, in
Sonderfällen und bestimmten Bezugssystemen auch nichtelektrische Arbeit
in die Definition der Ringspannung einzubeziehen, eine Arbeit, die in
anderen BZS vielleicht wirklich eine elektrische Arbeit ist (wie beim bewegten
Leiterstab im Magnetfeld).
Das dürfte für manchen Leser neu sein. Gerechtfertigt wird dies durch
die so erreichte Konsistenz zwischen den Aussagen verschiedener BZSe und
die experimentelle Tatsache, dass bei der Induktion auch in BZSen ohne
geschlossene elektrische Feldlinien ein Ringstrom fließt, der nicht die
Folge eines reinen Potenzialfelds sein kann.





