Die
Versuche können mit billigen Polarisationsbrillen
1)
oder mit simulierten Experimenten im
Schülerversuch durchgeführt
werden. Ein LCD-Bildschirm (BS) kann als
polarisierende Lichtquelle (PO) dienen. Vgl. auch: Die
quantenmechanische Messung mit polarisierten Photonen (Realexperiment
mit Polfiltern). Ein Polarisator für Licht bzw. Photonen hat zwei
Ausgänge: entweder tritt das Photon mit einer
Polarisation aus, die der Orientierung des Polarisators entspricht, oder
es wird vom Polarisator absorbiert.
Wenn
mittels eines Polarisators an ein einzelnes hindurch getretenes
Photon die Frage nach seiner Polarisation gestellt wird, erhält
man immer ein eindeutiges Ergebnis: immer die
Polarisation parallel zur Orientierung des Polarisators. Ob dies
auch die Polarisation vor dem
Durchtritt war, ist zu klären. Es handelt sich auf jeden
Fall um die Polarisation nach dem Durchtritt.
©
Horst Hübel, Würzburg 2015. Die
Darstellung orientiert sich grob am Buch J.J. Sakurai, Modern
Quantum Mechanics.
|
|
|
|
|
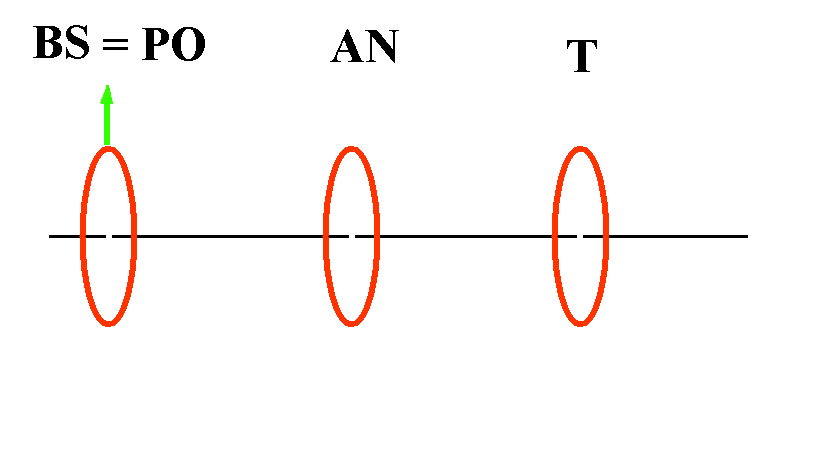
| Abb. 1
Der registrierte Durchtritt durch einen Polarisator PO
(evtl. = Bildschirm BS) stellt eine Messung
dar. Danach hat das passierende Photon die
be-stimmte
Eigenschaft
„polarisiert bzgl. der Richtung PO“.
Woher weiß man das? Ein Analysator AN zeigt es. Siehe
Abb. 2! |
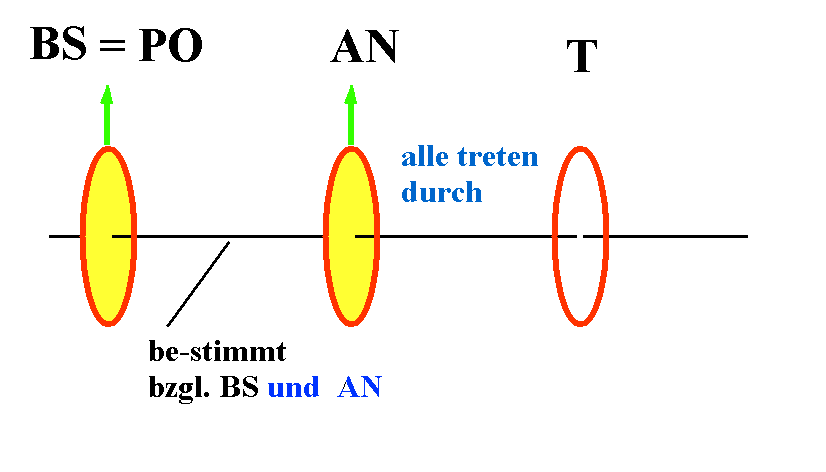
Abb.
2
Alle
Photonen mit be-stimmter Polarisation bzgl. PO treten
durch einen parallel ausgerichteten Analysator AN
hindurch, keine durch einen dazu senkrechten. Die Photonen
haben
also be-stimmte
Polarisation bzgl. PO als
Eigenschaft.
Die Messung durch PO ist reproduzierbar.
|
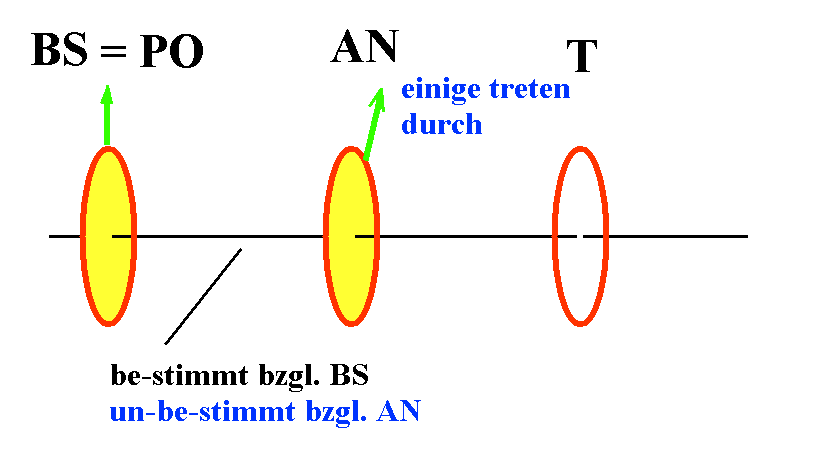
Abb.
3
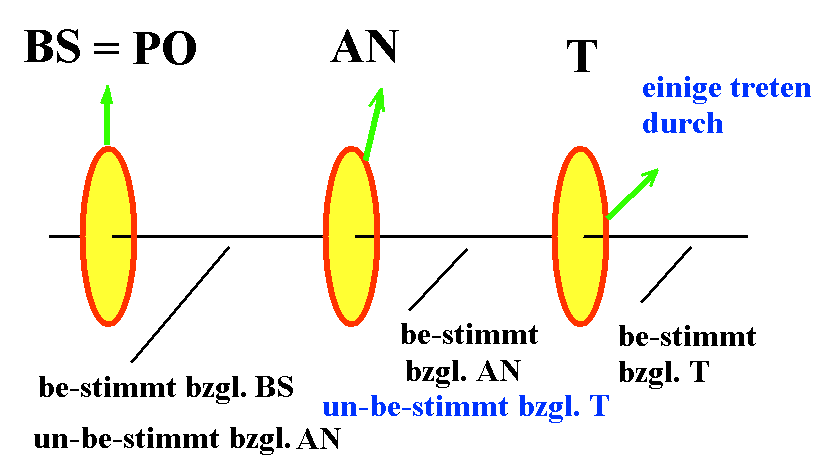
Bei schräggestelltem AN haben aus PO austretende
Photonen vor
AN un-be-stimmte
Polarisation bzgl. AN, erkennbar daran, dass bei
beliebiger Schrägstellung nicht alle Photonen AN
passieren können.
Einige
Photonen treten objektiv
zufällig
durch AN mit objektiven
Wahrscheinlichkeiten.
"Objektiv"
heißt dabei, dass auf keine Weise festgestellt werden
kann, weshalb ein Elektron durchgetreten ist und ein
anderes nicht. Von "subjektivem" Zufall würde man
sprechen, wenn man den Grund prinzipiell feststellen
könnte, aber es nicht getan hat.
|
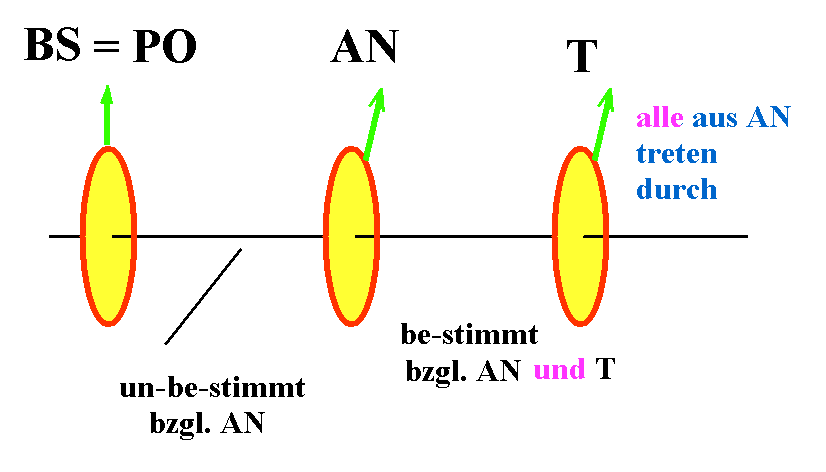
Abb.
4
Der
Durchtritt
eines Photon durch den Analysator mit der Richtung AN
stellt wieder eine Messung der Polarisation dar. Nach
dem Durchtritt besitzt
das
Photon mit Sicherheit die Eigenschaft „polarisiert
bzgl. AN“.
Ein
zu AN gleich gerichteter Polarisator T
(„Tester“)
bestätigt das, auch ein zu AN senkrecht orientierter.
|
|
|
|
|
|
| Abb. 5 Aus
einem Versuchsergebnis (Durchtritt eines Photons durch AN)
lässt sich nicht auf eine Eigenschaft vor der
Messung schließen: Bei
fast allen Orientierungen von PO treten durch AN (und T)
Photonen durch. |
Abb.
6 Die Eigenschaften „polarisiert bzgl. PO“
und „polarisiert bzgl. AN“ können nicht gleichzeitig
be-stimmt sein. Sie sind komplementär zueinander.
|
Abb.
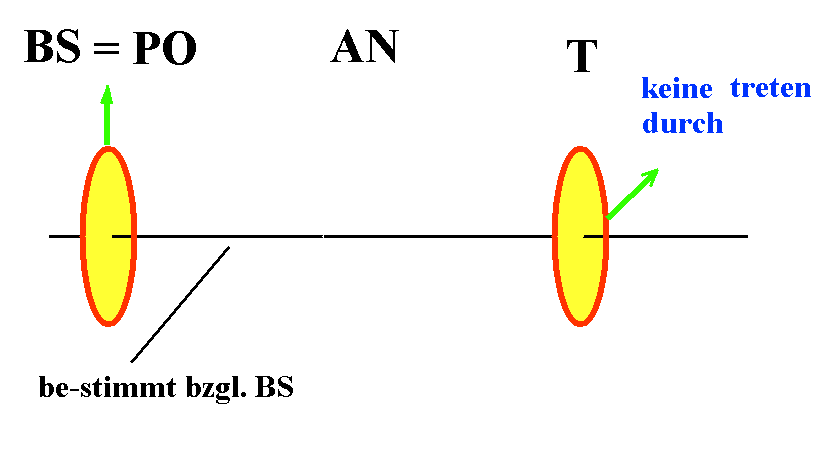
7 PO
⊥
T: Nach
Durchtritt
durch AN haben die Photonen die frühere Polarisation
bzgl.PO „vergessen“. Sonst würden keine Photonen durch T
hindurch treten.
|
Abb. 8
erläutert dabei die
Wirkung von AN in Abb. 7: „Quantenradierer“, der frühere
Informationen(PO) auslöscht (PO
⊥
T).
|
Download PDF-Datei
Man
kann mit Methoden2) der Quantenelektrodynamik3)
nachweisen, dass sich einzelne Photonen weitgehend genauso verhalten wie
klassische elektromagnetische Wellen. Wesentlicher Unterschied ist, dass
bei klassischen elektromagnetischen Wellen das statistische Verhalten der
Photonen nicht auffällt.
| E |
Bereits bei diesem
einfachen Experiment sind einige Grundfakten der Quantenphysik
erkennbar. (Sie werden allerdings durch diese Experimente
nicht bewiesen.)
|
| Zusammenfassung:
1. Licht besteht aus einzelnen Photonen, Photonenzwillingen
oder anderen Zuständen des elektromagnetischen Feldes.
2. (Einzelne) Photonen haben stets folgende Eigenschaften:
Teilchenzahl 1, elektrische Ladung q = 0, Masse m0 =
0 und Spinkomponente h
oder -h
(bzgl. einer Bezugsrichtung). Bei Photonenzwillingen ist die
Teilchenzahl stets 2.
3. Eine ideale Messung einer "klassisch denkbaren Eigenschaft"
liefert stets ein eindeutiges, be-stimmtes Ergebnis.
4. Durch eine Messung wird der Zustand eines Quantenobjekts in
der Regel verändert: Aus einer un-bestimmten
Eigenschaft wird eine be-stimmte.
5. Messungen be-stimmter Eigenschaften an Quantenteilchen sind
reproduzierbar.
6. Eine Quantenobjekt kann nicht alle "klassisch denkbaren
Eigenschaften" gleichzeitig haben. Eine Eigenschaft, die ein
Quantenobjekt in einem gegebenen Zustand besitzt, heißt be-stimmt
(mit einem be-stimmten Wert). Manche andere Eigenschaft dagegen
ist in dem gegebenen Zustand un-bestimmt6).
7. Wiederholte Messungen un-bestimmter Eigenschaften liefern statistisch
streuende Messwerte. Es handelt sich um objektiven
Zufall. Sie werden beschrieben durch objektive
Wahrscheinlichkeiten.
8. Es gibt Paare von Eigenschaften, die nicht gleichzeitig
be-stimmt sein können. Eine Eigenschaft kann dann be-stimmt
sein, während die andere un-bestimmt ist. Solche Eigenschaften
heißen komplementär.
|
1)
ideale Polarisatoren
vorausgesetzt;
2) Das
"freie" Photon der Quantenelektrodynamik
3)
Horst Hübel, Photon experiments for schools in the light of quantum
electrodynamics
4)
V21b Veranschaulichung von Grundfakten
der QM mit dem Elektronenspin
G47c Einige Grundfakten von Quantenobjekten
5)
Um das einzusehen, braucht
man nicht auf halbklassische Modelle wie das "Heisenberg-Mikroskop"
zurückgreifen. Mit diesem Modell wird manchmal die Komplementarität von
Ort und Impuls/Geschwindigkeit eines Elektrons (bzw. die Heisenberg'sche
Un-bestimmtheits-Relation) durch mechanische Stöße bei der Beleuchtung mit
Photonen plausibel gemacht.
6) Ein alternativer Zugang zu
Un-bestimmtheit und Be-stimmtheit liegt dem Konzept des Welle-Teilchen-Dualismus
zugrunde. Leider hat dieser historisch zu vielen
Interpretations-Missverständnissen geführt, vor allem in schulischen und
populärwissenschaftlichen Texten.