Bei Röntgenstrahlen, Elektronen- oder Neutronenstrahlen u.a. ist die Wellenlänge so gering (typisch 10^-10 m), dass sich Beugungsgitter oder Doppelspalte vergleichbarer Dimensionen (z.B. Spaltabstand) technisch nur schwer herstellen lassen. Aber die Natur stellt geeignete Beugungsobjekte in Form von Kristallen bereit, in denen die Atome, Ionen oder Moleküle, allgemein Gitterbausteine, in ein regelmäßiges Kristallgitter eingebaut sind mit einer Gitterkonstanten von typisch d = 3·10^-10 m. Es handelt sich um ein Raumgitter mit regelmäßigen Abständen in allen drei Dimensionen.

Umgekehrt kann man für die Kristallgitter-Beugung von Atomen auch Lichtgitter oder Mikrowellengitter aus stehenden elektromagnetischen Wellen herstellen mit Gitterkonstanten in der Größenordnung der Wellenlänge, also typisch 0,5 µm bzw. 1 mm .

Im Modell-Versuch kann man mit stark vergrößerten Wellenlängen und Gitterkonstanten arbeiten, z.B. mit Ultraschall-Wellen mit λ = 8 mm bzw. Mikrowellen mit λ  = 3 cm.  (vgl. Modellversuch mit Ultraschallwellen)

.

Bragg-Theorie der Kristallgitter-Beugung:

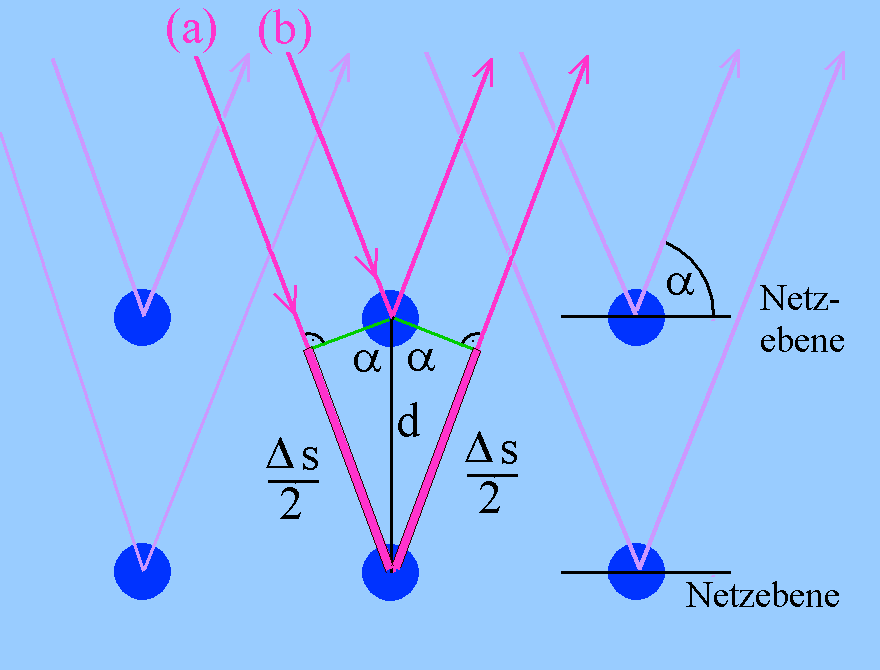Abb. 1: Monochromatische parallele Strahlung falle auf einen Einkristall mit regelmäßig angeordneten parallelen Netzebenen mit dem Abstand d. Die Strahlung wird an den einzelnen Gitterbausteinen in alle Richtungen gebeugt und interferiert im günstigen Fall in großer Entfernung vom Kristall. Die zu einem Maximum gelangende Strahlung trifft dort also quasi parallel ein. Das Maximum entsteht dadurch, dass dort eintreffende Strahlung einen Gangunterschied von n·λ (n ε Z) hat. Welche Gitterbausteine könnten dazu beitragen? Wir greifen uns zwei direkt benachbarte Gitterbausteine in zwei direkt benachbarten Netzebenen heraus. Sie werden von zwei einfallenden Strahlen (a) und (b) "getroffen", beugen nach allen Seiten, unter anderem in zwei parallele Richtungen, unter denen sie beobachtet werden. Es entstehen zwei Gangunterschiede Δs/2: einer vor den beiden Gitterbausteinen, ein gleicher nach den beiden Gitterbausteinen.

Der Gangunterschied der beiden Strahlen insgesamt ist

Bei einem bestimmten Winkel α beträgt er gerade n·λ (n ε Z). Die beiden Strahlen interferieren dann also konstruktiv. Aber das gilt auch für alle anderen so benachbarten Gitterbausteine, auch tief im Inneren des Kristalls, wenn die Strahlung nicht vorzeitig im Kristall absorbiert wird. Alle diese Strahlen überlagern sich in der Beobachtungsrichtung zu einem Maximum.

Es sieht dann so aus, als werde die Strahlung an den vielen parallelen Netzebenen reflektiert. Aber das geschieht eben nur für bestimmte Einfallswinkel α. Deswegen:

Ein so bestimmter Winkel α gegenüber den Netzebenen heißt Glanzwinkel.

(Sonst werden in der Optik stattdessen der Einfallswinkel und Austrittswinkel jeweils gegenüber dem Lot verwendet!)

Ist es denn gesichert, dass Einfalls- und Austrittswinkel immer gleich sind? Nein, keineswegs! Aber für andere geeignete Winkel existiert ein anderer paralleler Satz von Netzebenen, zum oben gewählten Satz geneigt, so dass an ihm wieder Bragg-Reflexion stattfinden kann. Die Winkel gegenüber dem oben gewählten Satz paralleler Netzebenen sind dann unsymmetrisch.

Beachte: Es handelt sich um keine echte Reflexion. Und: es sind im Prinzip alle Gitterbausteine in allen Netzebenen beteiligt, anders als manche Schulbücher suggerieren wollen!

Den "Wellencharakter" von Röntgenstrahlen, Elektronen- oder Neutronenstrahlen u.a. kann man auch anders nachweisen: Durch Beugung und Interferenz an ebenen Schichten mit regelmäßig angeordneten Beugungsobjekten ("Kreuzgitter-Interferenz") oder an Doppelspalt bzw. dünnen Drähten. In allen Fällen muss der Abstand der beugenden Strukturen in der Größenordnung der Wellenlänge sein.

In der Schule könnte bei "Elektronenbeugungs-Experimenten" mit der Elektronenbeugungsröhre der Lehrmittelfirmen statt Kristallgitter-Interferenz (wie an dreidimensionalen Graphit-Kristalliten) auch Kreuzgitter-Interferenz an ebenen Strukturen regelmäßig angeordneter Sechsecksringe (ähnlich wie Graphen) eine Rolle spielen, worauf Rode hingewiesen hat. Auch die Interferenz am Doppelspalt nach Jönsson  oder an einem "elektrostatischen Biprisma" (nach Möllenstedt) wird in der Schule diskutiert.

Nachweis des Wellen- bzw. elektromagnetischen Charakters der Röntgenstrahlen und zugleich der Kristallstruktur

Der gelungene Versuch von Walter Friedrich und Paul Knipping 1912 mit CuS nach einem Vorschlag von Max von Laue (Nobelpreis 1914) hatte zunächst eine Doppelfunktion: Er bestätigte die Vermutung von Laues, dass Röntgenstrahlen Wellenstrahlen "seien", und dass in einem Kristallgitter Atome, Moleküle, ... in einem Raumgitter regelmäßig angeordnet seien. Laue schloss sogar, dass es sich wie bei sichtbarem Licht um elektromagnetische Wellen handle. Für Röntgenstrahlen gilt demnach das, was auch für Licht gilt: Es lässt sich durch ein "Wellenmodell" und durch ein "Teilchenmodell" beschreiben. Die Quantentheorie macht dazu genauere Aussagen, auch für Elektronen- oder Neutronenstrahlen.

.

Untersuchungsmöglichkeiten:

• Gitterstruktur, insbesondere Netzebenenabstand
• magnetische Eigenschaften der Gitterbausteine (mit Neutronen)
• Ladungsverteilung in den Kristallen
• Wellenlängenmessung der einfallenden Strahlung

M. Rode, „Beugung an zweidimensionalen Gittern als Modell für die Elektronenbeugung“ in MNU journal, 75(4) (2022), 309 - 314; dazu:

H. Hübel, (2023). Kommentar dazu

H. Hübel, (2023). Elektronenbeugung am ebenen Kreuzgitter

.

( Juni 2014, Juni 2023 ergänzt)