Vgl. Bragg-Reflexion - mit Ultraschall und mit Photonen und Elektronen

	(1) Betrachten Sie klassische Wellen, z.B. Schall-, Ultraschall- oder Mikrowellen. Die klassischen Wellen sollen als paralleler Strahl auf ein Raumgitter mit periodisch in den drei Koordiantenrichtungen angeordneten Streukörpern einfallen. Diese entsprechen in atomaren Dimensionen den Atomen, Ionen, Molekülen, ... eines Kristalls. Das soll als Modellversuch zur realen Bragg-Streuung an Kristallen dienen. Dazu könnten mechanische Modelle mit periodisch angeordneten Kugeln (für Ultraschall) oder Metallplättchen (für Mikrowellen) geeignet sein.
(2) Betrachten Sie zwei benachbarte Strahlen, die gegen die Zentren zweier benachbarter Streukörper auf benachbarten Netzebenen gerichtet sind [(a) und (b)]. Von den Streuzentren gehen Huygenssche Elementarwellen aus, die kugelförmig die Streuzentren umgeben und sich radial ausbreiten. Unter den vielen Ausbreitungsrichtungen sind sicher auch die, die in der Zeichnung eingetragen sind. Sie treten wieder parallel aus dem Modell-Kristall aus und interferieren in großer Entfernung und überlagern sich dort konstruktiv oder destruktiv. Ganz entsprechend lassen sich auch für alle anderen Streuzentren benachbarte Strahlen finden, die in großer Entfernung sich in gleicher Weise überlagern. 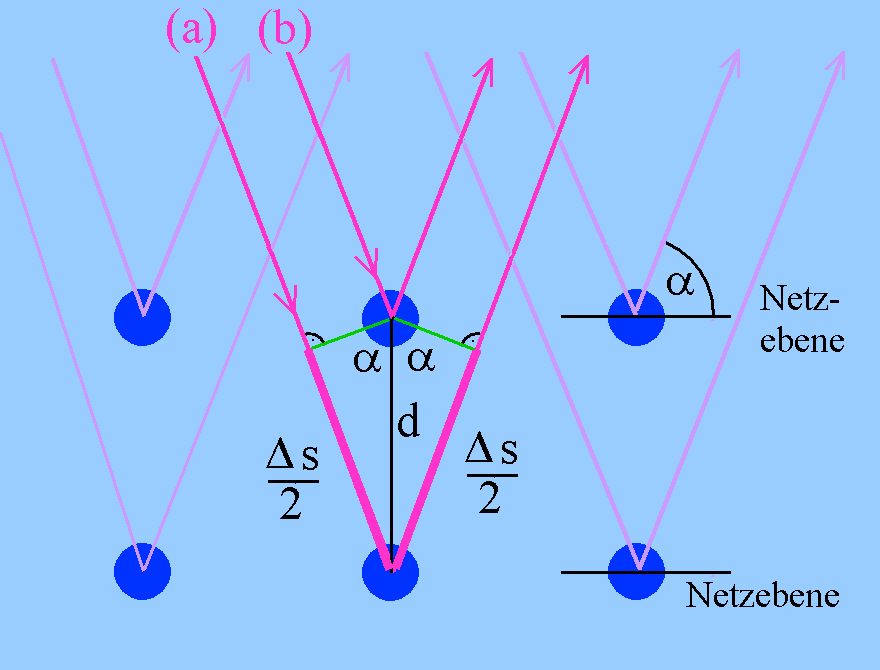Der  Strahl (a) muss zum Ort der Überlagerung einen längeren Weg zurücklegen. Gegenüber dem Strahl (b) hat er einen Wegunterschied Δs. Aus der Zeichnung ergibt sich:	(3)            Δs = 2 · d · sin(α) Wenn dieser Wegunterschied gerade ein ganzzahliges Vielfaches der Wellenlänge ist, findet immer konstruktive Interferenz statt. Da in einem Kristall sehr viele solcher benachbarten Paare von Strahlen beteiligt sind, entstehen sehr "scharfe", eng begrenzte Maxima hoher Intensität, dazwischen sehr breite Minima mit geringer Intensität. Wir haben also die Interferenzbedingung für Maxima (Bragg-Gesetz):  2·d·sin(α) = k·λ   k ganzzahlig Der Winkel α kann auch aufgefasst werden als Winkel zwischen dem einfallendem Strahl und der beteiligten "Netzebene". Er heißt dann üblicherweise Glanzwinkel.
(4) Es ergibt sich, dass dann, wenn überhaupt ein Maximum entsteht, bzgl. einer bestimmten Netzebene das Reflexionsgesetz erfüllt ist. Wenn sonst das Reflexionsgesetz erfüllt wäre, findet keine nennenswerte Streuung statt, wenn nicht für irgendeine Netzebene das Bragg-Gesetz erfüllt ist. Deshalb spricht man nicht von Reflexion, sondern nach ihrem Entdecker von "Bragg-Reflexion".

E

1. Das Auftreten scharf begrenzter Maxima bei bestimmten Glanzwinkeln und für bestimmte Wellenlängen ist typisch für Wellen, die auf ein Raumgitter einfallen. 2. Es sieht so aus, als werde die einfallende Wellenstrahlung an Netzebenen reflektiert. Tatsächlich unterscheidet sich die so genannte Bragg-Reflexion von einer wirklichen Reflexion dadurch, dass dies nur für ganz bestimmte Glanzwinkel geschehen kann. ("Bragg-Reflexion", aber keine Reflexion)

Auch an ebenen Kreuzgittern ist Interferenz von Röntgen-, Elektronen- oder Neutronenstrahlen etc. denkbar. Üblicherweise wird in der Schule das beobachtete System von Interferenzringen infolge Elektronenbeugung mit der Raumgitter-Interferenz an unterschiedlich orientierten Graphit-Kristalliten erklärt. Rode schlägt stattdessen vor, dass in der Elektronenbeugungsröhre der Schulphysik Kreuzgitter-Interferenz an graphen-ähnlichen ebenen Schichten von Sechsecksstrukturen stattfinden könnte. Die Theorie dazu finden Sie hier: