|
Wirbelfelder und
Potenzialfelder
|
.
.
Weil solche Felder für das Verständnis von elektrischen Stromkreisen eine
Rolle spielen, und weil hier viele Irrtümer kursieren, werden sie hier
näher erläutert. Verallgemeinernd geht es dabei um beliebige Felder, die
vom Ort x abhängen. "Dissipative" Vorgänge, bei denen Wärme frei
gesetzt wird, sind bei der Beurteilung von Potenzialfeld oder Wirbelfeld
ausgeschlossen. Vgl. Ringspannung
bei
der Induktion
Wenn man Kraftfelder im Auge hat,
sind Verschiebungsarbeiten der entscheidende Begriff. In allgemeineren
Fällen steht statt der Verschiebungsarbeit ein "Umlaufsintegral",
das hier nicht näher untersucht werden soll.
Es wird dabei immer wieder um einen Probekörper gehen.
Das könnte eine kleine Probemasse bzw. eine kleine positive Probeladung
sein. Sie soll (gedanklich) so klein gemacht werden, dass sie das
vorhandene Feld nur unwesentlich verändert.
.
Was ist ein Potenzialfeld?
Beispiele sind das Gravitationsfeld einer Kugelmasse, das
Gravitationsfeld über der (als eben betrachteten) Erdoberfläche, das
elektrische Feld in einem geladenen Kondensator, das elektrische Feld
zwischen einzelnen festgehaltenen elektrischen Ladungen.
Typisch für ein solches Potenzialfeld ist die Wegunabhängigkeit
der Verschiebungsarbeit *)
durch eine äußere Kraft
(die Verschiebungsarbeit durch die Feldkraft hätte einfach das
umgekehrte Vorzeichen; ich glaube, dass sich mit der äußeren Kraft etwas
einfacher argumentieren lässt). Verschiebt man eine Probemasse m bzw.
eine Probeladung q von einem Punkt A zu einem Punkt B, so muss für jeden
beliebigen Weg von A nach B dieselbe Verschiebungsarbeit verrichtet
werden. Das hat zur Folge, dass die Verschiebungsarbeit für jeden
beliebigen geschlossenen Weg (z.B. von A nach A) verschwindet. Zwar kann
es sein, dass für einen Teilweg eine positive Verschiebungsarbeit
aufgewendet werden muss. Diese wird aber auf anderen Wegstücken wieder
zurückgewonnen. Wir können auch sagen, dass auf letzteren Wegstücken negative
Verschiebungsarbeit aufgewendet wird.
So kann man keine Energie gewinnen oder verlieren, wenn man im
Gravitationsfeld über der Erdoberfläche eine Masse erst anhebt und dann
wieder zum Ausgangspunkt zurückfallen lässt. Genauso wenig kann im
Zwischenraum eines geladenen Kondensators Energie gewonnen oder verloren
werden, wenn man eine positive elektrische Ladung erst in Richtung der
positiven Kondensatorplatte verschiebt (wozu positive Verschiebungsarbeit
aufgewendet werden muss) und dann wieder auf den Ausgangspunkt
zurückfallen lässt. Bei letzterem Vorgang wird genau die vorher hinein
gesteckte Energie wieder zurückgewonnen.
Ein Potenzialfeld ist energieerhaltend, d.h. es kann keine Energie
gewonnen oder vernichtet werden. Erfolgt die Verschiebung durch die
Feldkraft so, dass Energie abgegeben wird, z.B. in Form von Wärme, dann
nimmt die Energie im Potenzialfeld ab. (In dieser Situation liegt streng
genommen kein Potenzialfeld mehr vor.) Das könnte z.B. so geschehen, dass
Ladungen durch einen Leiter mit Widerstand transportiert werden, wie etwa
bei der Entladung eines Kondensators über einen Widerstand. Energiezufuhr
von außen erfordert Abweichungen vom Potenzialfeld, ein Wirbelfeld.
Ein Feld, das an "Ladungen" entspringt und an "Ladungen" endet, das
"Ladungen" als Quellen und Senken hat, wird auch als ein Quellenfeld bezeichnet.
Im
Falle der Gravitation sind diese "Ladungen" Massen, im elektrischen Fall
echte elektrische Ladungen. Ein Potenzialfeld ist zugleich ein
Quellenfeld.
In einem solchen Feld hat eine Probemasse m bzw. eine Probeladung q an
einem Ort x eine potenzielle Energie, die nur von der
Position x des Probekörpers im Potenzialfeld abhängt: Um den
Probekörper von einem beliebigen festen Punkt A zu irgendeinem
Punkt x zu verschieben muss immer die gleiche Arbeit verrichtet
werden. Sie ist dann als potenzielle Energie im Probekörper gespeichert.
Die Position x ist ein Maß für sie. Dementsprechend ist auch das
Potenzial Φ(x) selbst als potenzielle Energie pro "Ladung" eine
eindeutige Funktion des Orts x. Müsste man für die Verschiebung
vom festen Punkt A zum Punkt x bei unterschiedlichen Wegen jeweils
eine andere Arbeit aufwenden, hätte es keinen Sinn, dem Probekörper am
Punkt x eine potenzielle Energie zuzuordnen.
Im Potenzialfeld lässt sich eine Spannung zwischen zwei Punkten A und B
definieren: Es handelt sich um die spezifische Arbeit beim Verschieben
einer "Ladung" von A nach B durch eine äußere Kraft bzw. um das
Potenzial Φ(B) an der Stelle B im Vergleich zum Potenzial Φ(A) an der
Stelle A. "Spezifisch" heißt dabei "pro Ladungsmenge", also im
elektrischen Fall U = WAB / q bzw. U = [ Φ(B) - Φ(A) ] .
Man kann die Spannung U auch definieren als die spezifische Arbeit beim
Verschieben einer "Ladung" von B nach A durch die Feldkraft bzw.
um das Potenzial Φ(A) an der Stelle A im Vergleich zum Potenzial Φ(B) an
der Stelle B. "Spezifisch" heißt dabei "pro Ladungsmenge", also im
elektrischen Fall U = WBA / q bzw. U = - [ Φ(B) - Φ(A) ] .
Gleichgültig, wie man definiert: Verbindet man den (Minus-)/Masse-Pol des
Spannungsmessers mit dem negativen Pol, so zeigt der Spannungsmesser bei
Verbindung mit dem Pluspol einen positiven Wert an. Deswegen spricht man
nur von einer Spannung "zwischen A und B".
U = [ Φ(B) - Φ(A) ] ist an das Vorliegen eines Potenzialfelds gebunden. (
Andernfalls wäre ein formal nach U = WAB / q definiertes U
wegabhängig, also nicht sehr sinnvoll.). Das gilt z.B. in der
Elektrostatik.
Ein Potenzialfeld enthält selbst auch potenzielle Energie.
Energieerhaltung ist verletzt bei dissipativen Vorgängen, wenn z.B. Wärme
abgegeben wird.
.
Was ist ein Wirbelfeld?
 |
Bei einem Wirbelfeld ist im Gegensatz dazu die Verschiebungsarbeit
von einem Punkt A zu einem Punkt B wegabhängig.
Die Verschiebungsarbeit für einen geschlossenen Weg kann dann
von Null verschieden sein. Das kann bei fehlender Erfahrung zu
unerwarteten Effekten führen:
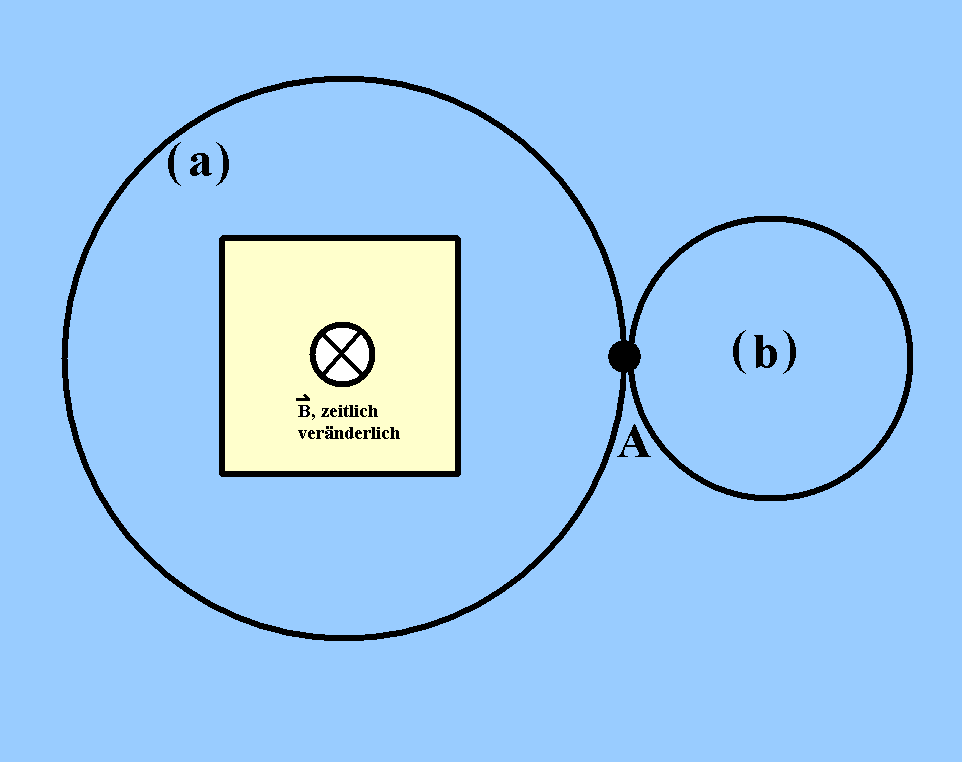
Betrachten Sie den Eisenkern einer Spule, die von einem
Wechselstrom durchflossen wird. Der Eisenkern soll so sein, dass
der gesamte magnetische Fluss auf den Kern beschränkt
ist.
Im Eisenkern entsteht dann ein magnetisches Feld von
wechselnder Größe und Richtung. Die Folge ist ein elektrisches
Wirbelfeld, das den Eisenkern ringförmig umgibt (Induktion). A
sei ein Punkt außerhalb des Kerns. Wir legen nun eine
geschlossene Leiterschleife durch A. Sie soll einmal den
Eisenkern umfassen (Fall a), ein andermal nicht (Fall b). Im
Fall b verrichtet das elektrische Wirbelfeld keinerlei Arbeit.
In der Leiterschleife entsteht also kein Induktionsstrom. Im
Fall a dagegen kann das elektrische Feld Arbeit verrichten,
durch die ein elektrischer Strom im Leiter entsteht. Die vom
Feld verrichtete Arbeit wird dann z.B. in Form von Wärme an die
Umgebung abgegeben.
|
| Abb. 1: Zwei geschlossene Stromkreise bei der Induktion,
aber nur im Fall a) ein Strom. |
|
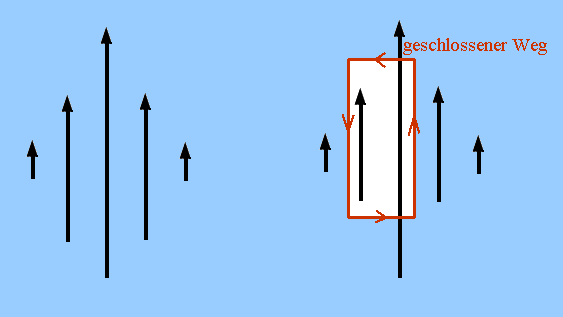 |
Abb. 2: Beispiel für ein Wirbelfeld ohne geschlossene
Feldlinien
Wir betrachten eine schmale geschlossene Kurve (rot), die
elektrische Feldlinien begleitet. Später wollen wir zu
infinitesimal kleinen Abmessungen übergehen. Auf den Wegstücken
senkrecht zu den Feldlinien kann keine Arbeit verrichtet werden,
wohl aber auf den parallel verlaufenden Stücken. In vielen
Fällen werden sich der Anteil zur Verschiebungsarbeit "gegen das
Feld" und der Anteil "mit dem Feld" gegenseitig aufheben.
Aber, wenn sich die Stärke des elektrischen Feldes "quer zur
Feldrichtung" ändert, gilt das nicht mehr. In diesem Fall ist
die Verschiebungsarbeit für diesen geschlossenen Weg von Null
verschieden und es liegt ein Wirbelfeld vor. Anschaulich ist
also typisch für ein Wirbelfeld eine "Queränderung der
Feldstärke".
|
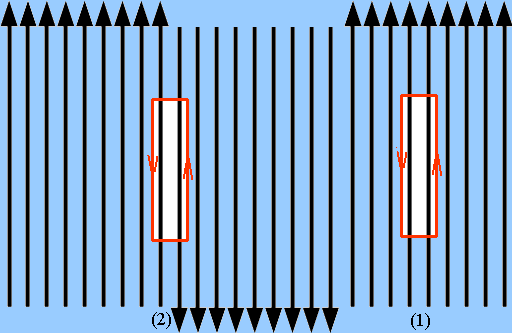 |
Abb. 3: Beispiel für ein Wirbelfeld
Wir betrachten eine schmale geschlossene Kurve (rot) aus
infinitesimal gedachten Strecken, die die elektrischen
Feldlinien begleitet. Bei Kurve (1) ist die Verschiebungsarbeit
0: Feld einmal mit, einmal gegen die Durchlaufsrichtung. Bei
Kurve (2) ist dagegen die Verschiebungsarbeit =/= 0, weil hier
die Felder auf Hin- und Rückweg immer entgegengesetzt zur
Durchlaufsrichtung orientiert sind. Wirbel entstehen in diesem
Beispiel an der Grenze zwischen Zonen mit entgegengesetzter
Feldrichtung.
|
In vielen Fällen ist ein solches Wirbelfeld ein Feld mit ringförmig in
sich geschlossenen Feldlinien. Dann handelt es sich um ein reines
Wirbelfeld ohne Anteil eines Potenzialfelds (div E = 0, rot
E =/= 0)#. Das muss aber nicht so
sein. Es sind auch Wirbelfelder denkbar mit einem überlagerten
Potenzialfeld. Dann könnten die Feldlinien Anfang und Ende haben (E
wäre dann auch ein Quellfeld), aber trotzdem eine Queränderung des Feldes
vorhanden sein, also div E =/= 0 und rot E =/= 0. Ein
typisches Beispiel ist ein auf einen bestimmten Bereich beschränktes Feld,
dessen Feldlinien parallel zur Begrenzung verlaufen (Abb. 2, 3). Nur ein
reines Wirbelfeld ist quellfrei.
In einem Wirbelfeld kann man der Probemasse m (Fall des
Gravitationsfelds) bzw. der Probeladung q (Fall des elektrischen Felds)
keine potenzielle Energie und kein Potenzial (im Sinne obiger
Definition, also ein "skalares" Potenzial) zuordnen, weil die Arbeit zur
Verschiebung von A nach B je nach Weg unterschiedlich ist.
Ein Potenzialfeld ist wirbelfrei.
| Wirbelfelder können
geschlossene Feldlinien haben (reines Wirbelfeld; quellfreies
Wirbelfeld). Es gibt auch Wirbelfelder mit Quellen und Senken bzw.
nicht geschlossenen Feldlinien. Sie sind oft auf einen endlichen
Raumbereich beschränkt. Sie lassen sich als Überlagerung von einem
Wirbelfeld mit einem Potenzialfeld deuten. |
| reines (quellfreies) Wirbelfeld E |
reines (wirbelfreies) Potenzialfeld E |
Überlagerung von quellfreiem Wirbelfeld und wirbelfreiem
Potenzialfeld E |
| Verschiebungsarbeit *) wegabhängig |
Verschiebungsarbeit wegunabhängig |
Verschiebungsarbeit nicht überall wegunabhängig |
| geschlossene Feldlinien |
Feldlinien beginnen an Quellen und enden an Senken des Felds |
|
| Es gibt kein Potenzial (und im Spezialfall: keine potenzielle
Energie) |
Potenzial existiert (und im Spezialfall auch: potenzielle Energie) |
Definition eines Potenzials (und im Spezialfall einer potenziellen
Energie) problematisch |
| rot E =/= 0 div E =
0 #. |
rot E = 0 div E =/=
0 |
rot E =/= 0 div E =/=
0 |
# Die Ausdrücke aus der
Vektoranalysis sollen hier nicht erläutert werden. Wer sie nicht kennt,
kann sie überlesen.
Beispiele
a) Feld eines geladenen
Plattenkondensators
Für jeden beliebigen geschlossenen Weg, ob er nun die felderzeugenden
Ladungen einschließt oder nicht, ist die Verschiebungsarbeit 0. Also
liegt ein Potenzialfeld mit einem Potenzial Φ(x)
vor. Eine Ladung in diesem Feld besitzt eine potenzielle Energie. Dieses
Feld kann Arbeit verrichten, indem es z.B. eine positive Probeladung vom
Pluspol abstößt und so beschleunigt, oder indem es dabei Wärme nach
außen abgibt. Aber die potenzielle Energie der Ladung ist schnell
aufgezehrt. Dann kommt der Vorgang zum Erliegen, außer wenn erneut
Energie von außen zugeführt wird. Verbindet man die Kondensatorplatten
durch einen Leiter (innerhalb oder außerhalb des Kondensatorvolumens),
dann wird ebenfalls potenzielle Energie in kinetische Energie der
verschobenen Ladungen bzw. Stromwärme umgewandelt bis alle Ladungen des
Kondensators abgeflossen sind. Damit endet der Vorgang.
.
|
Was hat man von dieser Kenntnis über das
Potenzialfeld eines geladenen Plattenkondensators?
|
- Energieumwandlungen, z.B. bei der Beschleunigung oder dem
Abbremsen von elektrischen Ladungen im Kondensatorfeld
werden erklärt. Das erlaubt z.B. auch die Berechnung der
Endgeschwindigkeit nach dem Beschleunigen durch ein
elektrisches Feld.
- Es wird ein nützlicher Zusammenhang zwischen
Spannung/Potenzial und potenzieller Energie einer Ladung zur
Verfügung gestellt. Gemeint ist die gewöhnliche Spannung als
Potenzialdifferenz pro Ladungsmenge.
- Es erklärt den Entladevorgang eines Kondensators.
- Verbindet man die beiden Kondensatorplatten im Außenraum
wird hier ein nicht stationärer (zeitabhängiger) Ringstrom
angetrieben 1. durch die Potenzialdifferenz zwischen den
beiden Platten (auf dem Weg im Außenraum) und 2. als
Verschiebungsstrom im Kondensator als Folge der zeitlichen
Änderung des elektrischen Felds im Kondensator.
|
.
b) Monozelle
Bei der unverbundenen Monozelle sorgen "chemische Kräfte",
also Kräfte nichtelektrischer Natur, für eine Ladungstrennung. Es
entstehen ein positiver und ein negativer Pol. Der Vorgang ist beendet,
wenn Kräftegleichgewicht zwischen den chemischen Kräften und der so
entstandenen elektrischen Kraft des E-Felds vom Pluspol zum
Minuspol (im Inneren der Monozelle) entstanden ist. Bringen wir
gedanklich eine weitere positive Probeladung in das Batterieinnere,
würde diese keine Kraft erfahren. Formal kann man die Wirkung der
chemischen Kräfte durch eine eingeprägte "elektrische" Feldstärke E(e)
beschreiben und sie dadurch in gleicher Weise wie die elektrischen
Kräfte behandeln, ein raffinierter Trick. Danach ist also das Innere der
unverbundenen Monozelle feldfrei, weil sich die eingeprägte elektrische
Feldstärke und die wirkliche elektrische Feldstärke gegenseitig
aufheben: E(e) + E = 0 im Inneren (E(e)
ist auf das Innere der Monozelle beschränkt; man kann dies auch als
Aussage über die beteiligten Kräfte sehen). Bei der unverbundenen
Monozelle kann man die formale "eingeprägte Feldstärke" E(e)
im Prinzip durch die sich im Inneren ausbildende elektrische Feldstärke
messen: E(e) = - E. Ist das Gesamt-Feld hier
wirbelfrei? Und es kommt auf das Gesamt-Feld an, weil dieses mit allen
wirkenden Kräften und Verschiebungsarbeiten zusammenhängt!
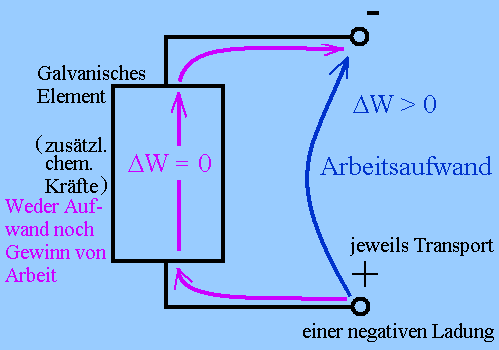 |
Abb. 4: Unterschiedliche Verschiebungsarbeit je nach
Weg
Überlegen wir uns wieder die Verschiebungsarbeit bei einem
vollen Umlauf: Startpunkt A liege auf dem positiven Pol. Um
die positive Probeladung im Außenraum zum negativen Pol zu
führen, wird Energie frei bzw. negative Verschiebungsarbeit
verrichtet. Um die Ladung durch das Innere zu A
zurückzuführen, muss keine Arbeit verrichtet werden. Die
gesamte Verschiebungsarbeit auf dem geschlossenen Weg ist
negativ.
Führen wir die positive Probeladung aber vom negativen Pol
durch den Außenraum zu A zurück, muss für den Rückweg
positive Arbeit aufgebracht werden, weil sich die beiden
positiven Ladungen abstoßen. Es ist plausibel, dass für den so
gewählten geschlossenen Weg die Verschiebungsarbeit 0 ist.
Es liegt ein Wirbelfeld vor, weil es geschlossene Weg gibt,
auf denen die Verschiebungsarbeit nicht 0 ist. Insgesamt haben
wir gesehen, dass die Verschiebungsarbeit wegabhängig ist. Es
liegt also kein Potenzialfeld vor. Allerdings verschwindet die
Verschiebungsarbeit nur bei speziellen Wegen durch das Innere
der Monozelle nicht.
Das ist möglicherweise der Grund, weshalb jeder Elektroniker
ungestraft und mit Erfolg von Potenzialen in seiner Schaltung
sprechen kann.
|
Eine Ringspannung U wird definiert als Verschiebungsarbeit für einen
geschlossenen Weg pro Ladungsmenge q. Bestenfalls für E allein
lässt sich ein Potenzial definieren. Ein evtl. vorhandenes überlagertes
Potenzialfeld kann zur Ringspannung nichts beitragen, nur E(e).
Nur Ringspannungen für einen Weg, der teilweise durch das Innere der
Monozelle führt, sind von 0 verschieden.
Wenn die Monozelle Teil eines geschlossenen Stromkreises ist, fließen
die an den Polen angehäuften Ladungen sofort wieder ab. Es kommt dann
nicht zur Ausbildung des Kräftegleichgewichts im Inneren der Monozelle.
Die chemischen Kräfte bzw. E(e) treiben dann einen Ringstrom
an. Die Unterscheidung Wirbelfeld oder Potenzialfeld ist dann aber
ohnehin uninteressant..
.
|
Was hat man von dieser Kenntnis über das
"elektrische" Wirbelfeld bei einer Monozelle?
|
- Sie erklärt, dass ein stationärer
Strom, der ständig Energie nach außen abgibt, in
einem Stromkreis mit einer Monozelle überhaupt fließen
kann. Nämlich deshalb, weil das Wirbelfeld E(e)
für ständigen Energienachschub sorgt. Dazu ist eben nur
ein Wirbelfeld in der Lage.
- In diesem Fall ist der Ringstrom eine Folge der
Ringspannung, die wiederum allein eine Folge des Wirbelfelds
E(e) ist.
- Es wird klar, dass es sich also um die ständige
Überführung einer nichtelektrischen Energie (mittels
chemischer Kräfte) in eine andere nichtelektrische
Energieform (Wärme) handelt.
- Es wird klar: Außerhalb der Monozelle bildet sich ohne
Stromfluss das gleiche elektrische Feld aus wie bei einem
auf die gleiche Spannung aufgeladenen Kondensator (bei
entsprechenden Dimensionen). Außerhalb - aber nur dort -
sind also Feld und Kräfte in diesem Fall von einem
Potenzialfeld nicht zu unterscheiden. Die Argumentation mit
einem Potenzialfeld genügt deshalb für viele
Anwendungsfälle, wie in der Elektronik.
- Es wird klar: Fließt der Ringstrom durch zusätzliche
Potenzialfelder, so spielen diese selbst keinerlei Rolle für
die Ringspannung, die nur durch die Monozelle bestimmt ist.
Der Ringstrom ist unabhängig von solchen Potenzialfeldern,
aber hängt vom jeweiligen Kreiswiderstand ab.
|
Der letzte Punkt ist z.B. bei einer Halbleiter-Diode
im Stromkreis zu beachten. Durch Raumladungen in der Nähe der
Grenzschicht entstehen dort zusätzliche elektrische Potenzialfelder.
Für die Ringspannung sind sie belanglos. Diese ist allein durch die
Monozelle bestimmt.
.
c) Induktion bei zeitlich veränderlichem Magnetfeld
Eine feste Leiterschleife werde von einem zeitlich veränderlichen
magnetischen Fluss durchsetzt. Nach dem Induktionsgesetz entsteht dann
ein elektrisches Wirbelfeld, das das sich ändernde Magnetfeld ringförmig
umgibt. Es handelt sich um ein reines Wirbelfeld, weil (wenn der
geschlossene Weg ganz homogen oder gar nicht mit einem Leiter belegt
ist) nirgends Quellen und Senken eines Potenzialfelds entstehen. Es
kommt auf den Verlauf des geschlossenen Weges an. Insbesondere könnte
der geschlossene Weg den magnetischen Fluss auch mehrfach umkreisen,
wobei die Verschiebungsarbeit mehrfachen Wert als bei einmaliger
Umkreisung haben würde. Trotz zeitlich veränderlichem Magnetfeld kann
man auch leicht Wege finden, bei denen die Verschiebungsarbeit für einen
geschlossenen Weg verschwindet (wenn der Weg keinen magnetischen Fluss
umfasst). Andernfalls gibt es eine Ringspannung U =/=
0, die bis auf das Vorzeichen gleich der Änderungsrate des magnetischen
Flusses ist. Die Ringspannung ruft im geschlossenen Stromkreis einen
Ringstrom I hervor. Erst, wenn man den Leiterkreis auftrennt, entsteht
durch die Ladungsverschiebung zwischen den entstandenen "Klemmen" ein
zusätzliches überlagertes Potenzialfeld und damit auch eine gewöhnliche
Spannung ("Klemmenspannung") von (weitgehend) gleicher Größe wie die
Ringspannung. Für den Stromfluss im geschlossenen Stromkreis ist aber
die Ringspannung U verantwortlich.
Auch hier kann ein evtl. vorhandenes überlagertes Potenzialfeld zur
Ringspannung nichts beitragen. Der Ringstrom I ist allein durch die
Ringspannung U und den gesamten Kreiswiderstand R bestimmt.
Anders als in der Elektrostatik verschwindet die elektrische
Feldstärke im Leiter (bei nicht zu großen Frequenzen des sich ändernden
Magnetfelds) i.A. nicht, da die Ladungsverschiebung durch den Stromfluss
nie zu einer Kompensation des elektrischen Feldes führt. Die Feldstärke
im Inneren des Leiters (oder: Kontinuitätsgleichung)
ist im Gegenteil für den ständigen (evtl. wechselnden) Strom
verantwortlich. In der Elektrostatik dagegen, z.B. bei einer geladenen
Kugel, werden in der Regel nur Situationen betrachtet, bei denen sich
der stationäre Zustand mit Feldstärke 0 im Leiter bereits eingestellt
hat.
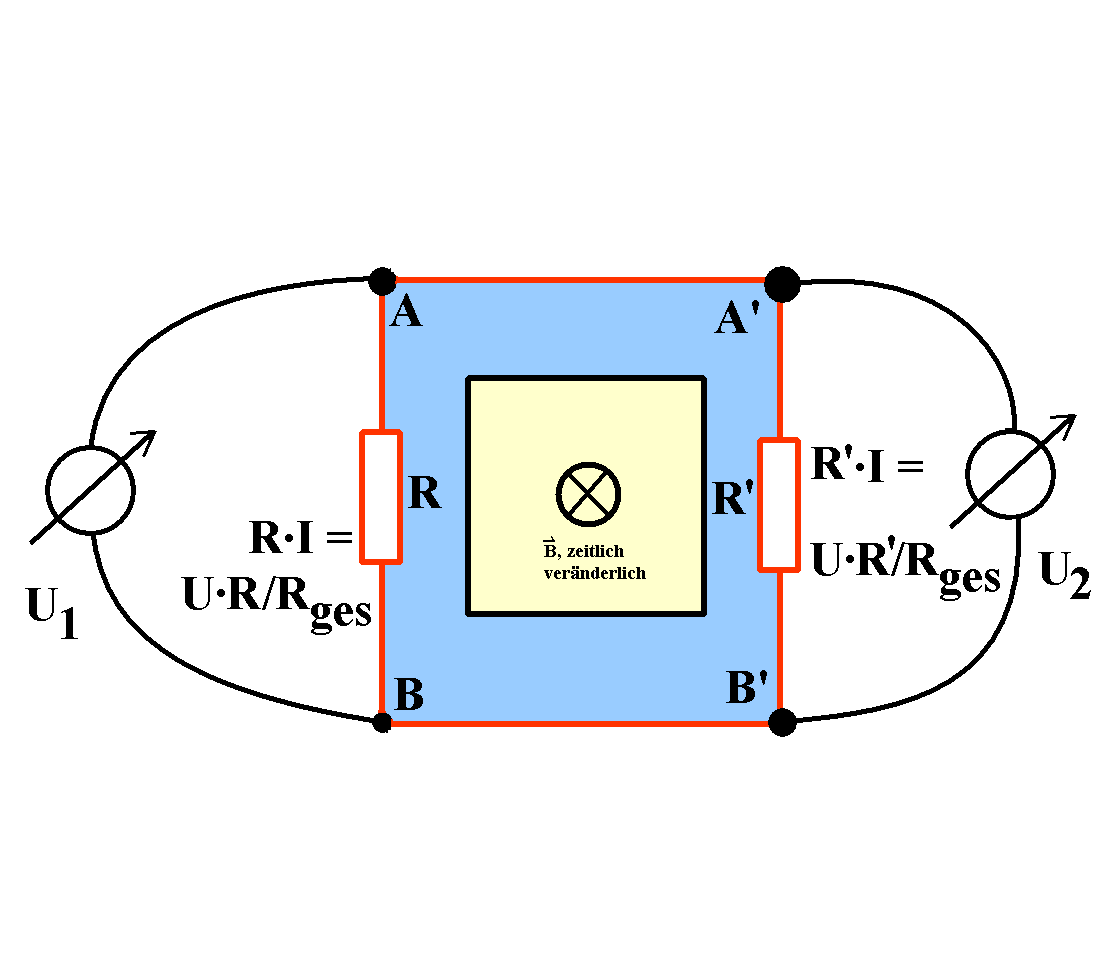 |
Abb. 5: Unterschiedliche Anzeigen der
Spannungsabfälle U1 und U2 bei gleicher
Ringspannung U, wenn R und R' unterschiedlich!
Vorausgesetzt sind hochohmige Spannungsmesser.
U1 misst den Spannungsabfall am Widerstand R, U2
den Spannungsabfall an R' infolge des Ringstroms I. U ist die
Ringspannung im rot gezeichneten Leiterkreis, wenn dieser ein
sich änderndes magnetisches Feld B einschließt. Sie
hat einen Ringstrom I zur Folge.
(Keiner der beiden Messkreise soll von einem nennenswerten
sich ändernden magnetischen Fluss durchsetzt werden.)
|
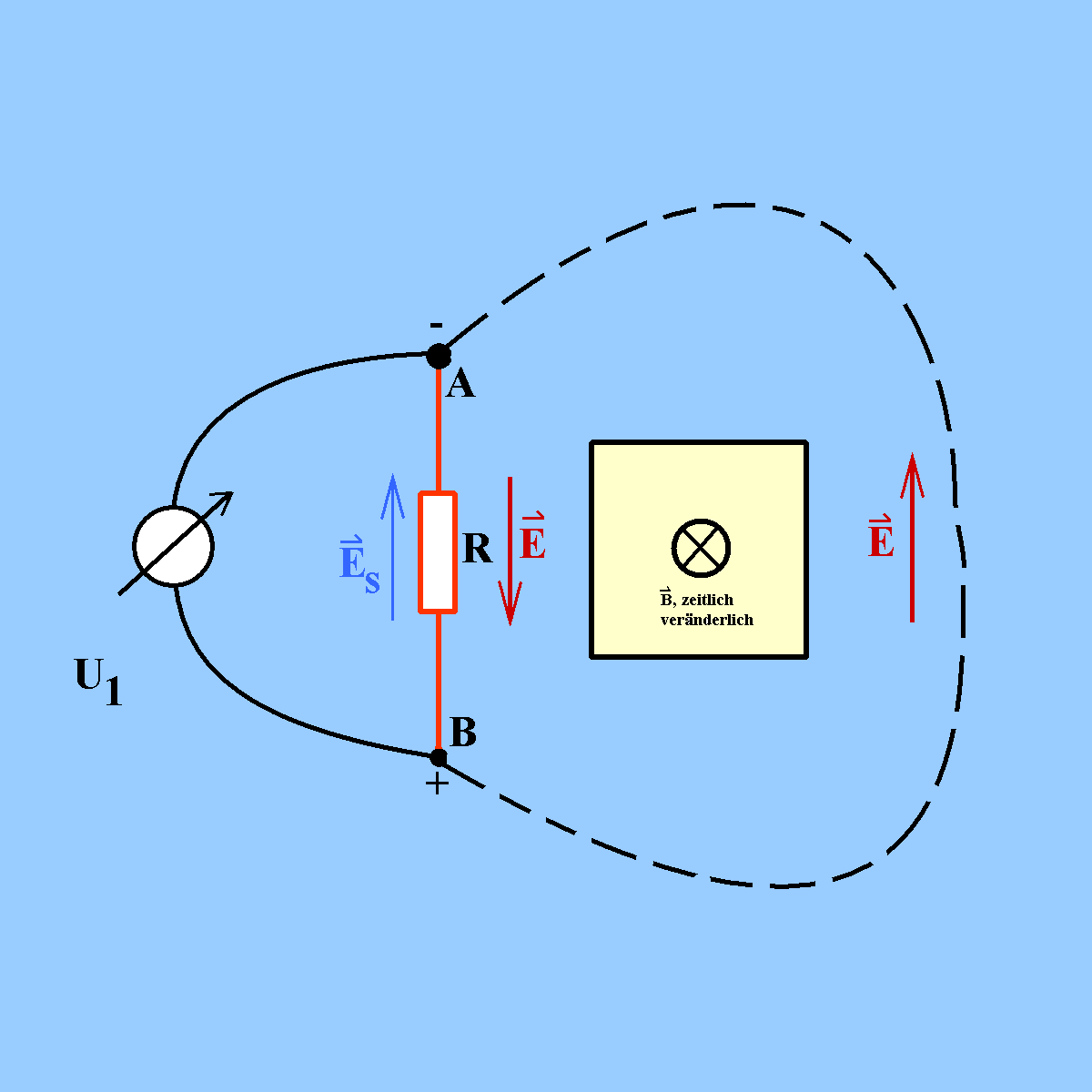 |
Abb. 6: Keine Anzeige, wenn ein nur gedachter
Leiterkreis vom sich ändernden magnetischen Fluss durchsetzt
wird.
(Der Kreis A - Voltmeter - B - Widerstand R - A soll ohne
magnetischen Fluss sein. Er wird hier Messkreis genannt. Das
könnte näherungsweise z.B. durch einen Eisenkern erreicht
werden, der den gesamten magnetischen Fluss einschließt/führt.)
U1 = 0, da 1. kein Ringstrom fließt, der einen
Spannungsabfall an R hervorrufen könnte, da 2. den Messkreis
kein sich ändernder magnetischer Fluss durchsetzen soll.
Oder:
U1 = 0 bei einer gedachten
Ergänzung zum geschlossenen Leiterkreis: Zwischen A und B
sorgt das Feld E zu einer Ladungsverschiebung (+ bei
B, - bei A), die zur Entstehung eines entgegengesetzten
sekundären elektrischen Felds Es
führt, bis sich schließlich die beiden Felder zwischen A
und B aufheben.
Diese Erklärung berücksichtigt die Tatsache,
dass auch in einem gedachten Kreis, der von einem sich
ändernden magnetischen Fluss durchsetzt wird, durch
Induktion ein elektrisches Wirbelfeld E entsteht.
Wegen der Kompensation durch das sekundäre elektrische
Feld Es
kann es nicht durch das Voltmeter nachgewiesen
werden.
|
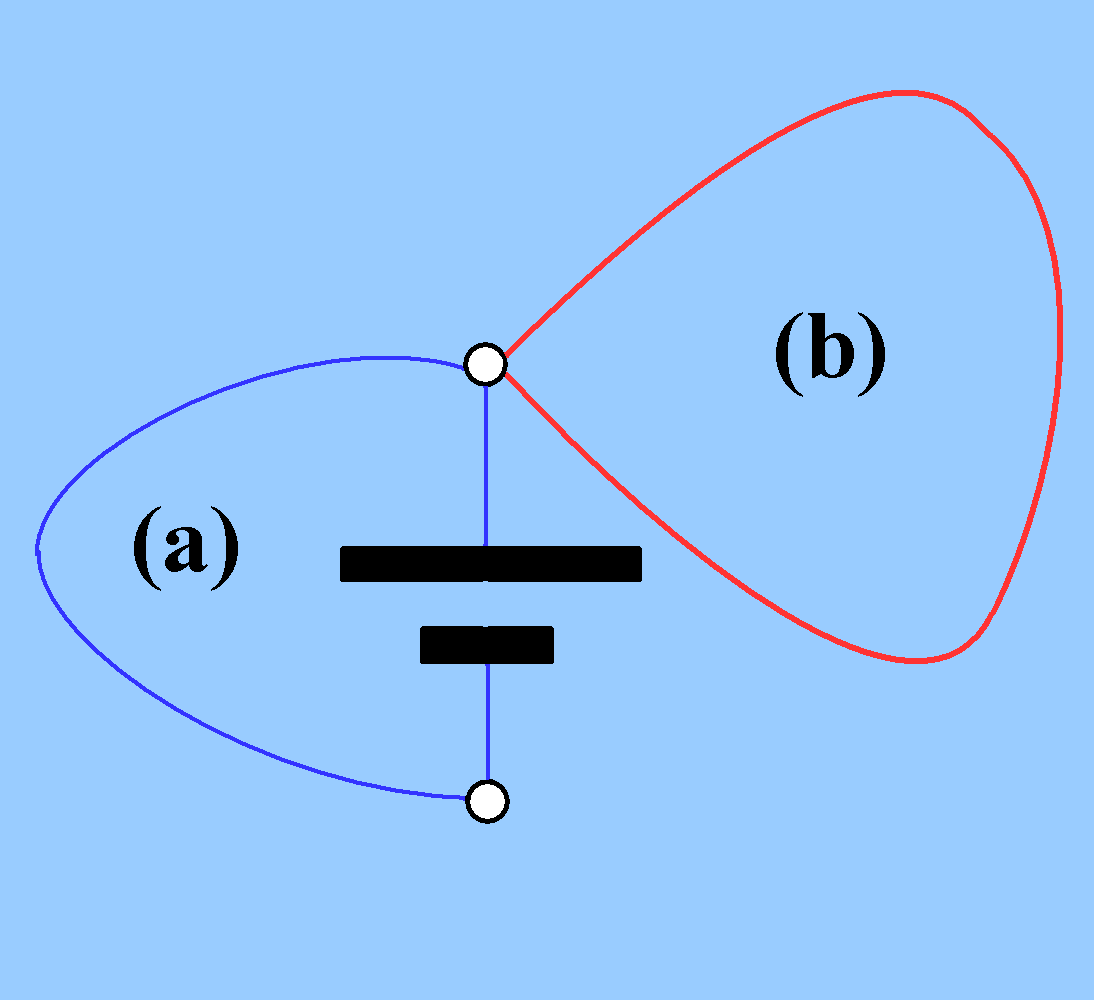 |
Abb. 7: Situation ohne Magnetfeld: Kein Strom bei (b),
obwohl ein geschlossener Leiterring vorliegt (alle Leiter sollen
einen endlichen Widerstand haben)
Analog zu den (magnetischen) Situationen (b)
Ringspannung 0, wenn kein magnetischer Fluss umfasst wird,
und (a) Ringspannung =/=0 , wenn ein sich zeitlich ändernder
magnetischer Fluss umfasst wird, kann man auch bei der
Monozelle zwei ähnliche Situationen finden:
(b), wenn der geschlossene Weg nicht durch die
beiden Pole der Monozelle verläuft, (a), wenn er durch beide
Pole verläuft. Nur im Fall a) erhält man einen Ringstrom,
wenn die beiden Pole längs des geschlossenen Wegs mit einem
Leiter endlichen Widerstands verbunden werden. Dass in einer
Situation mit Leitern ähnlich der Zeichnung links (Weg b)
kein Strom fließen kann, macht zwar Schülern im
Anfangsunterricht noch Schwierigkeiten, ist aber sonst so
selbstverständlich, dass man beide Situationen (a) und (b)
nicht getrennt herausstellen muss. Anders verhält es sich
bei der Induktion.
|
.
|
Was hat man von dieser Kenntnis über das
elektrische Wirbelfeld bei der Induktion?
|
- Das Grundsätzliche der Induktion wird herausgestellt: die
Entstehung einer Ringspannung bzw. eines elektrischen
Wirbelfelds bei der zeitlichen Änderung des eingeschlossenen
magnetischen Flusses.
- Die Ringspannung erklärt, wie die Klemmenspannung bei
unterbrochener Induktionsschleife entsteht.
- Das Induktionsgesetz dabei erklärt, weshalb
Spannungsmesser unterschiedliche Ringspannungen anzeigen bei
unterschiedlichen geschlossenen Kurven. Die Ringspannung ist
nur von 0 verschieden, wenn ein sich zeitlich ändernder
magnetischer Fluss umfasst wird.
|
Allerdings, es gibt Situationen (Induktion bei zeitlich konstantem
Magnetfeld), wo es zwar immer eine Ringspannung, aber in bestimmten
Bezugssystemen kein elektrisches Feld mit geschlosssenen Feldlinien
gibt. Die Aussagen hier gelten aus der "Sicht der betrachteten Kurve".
.
d) Induktion bei einem "im Magnetfeld bewegten" Leiterstab
Schwieriger ist der Fall einer Leiterbrücke (Leiterstab), die mit
gutem Kontakt auf einem U-förmigen Leiterbügel gleitet. Das Magnetfeld B
durchsetze das so aufgespannte Rechteck senkrecht. Manche Aussagen
hängen vom Bezugssystem (BZS) ab, in dem ein Vorgang betrachtet wird. Im
Laborsystem, in dem der U-förmige Leiterbügel ruht, können wir die
Induktion korrekt als Folge der Lorentz-Kraft FL
= q v x B beschreiben, der sich formal eine eingeprägte
Feldstärke E(e) = FL /q = v
x B zuordnen lässt (Im mit der Leiterbrücke mitbewegten BZS ist
das sogar eine echte elektrische Feldstärke E'). Das eingeprägte
Feld E(e) ist auf die mit der Geschwindigkeit v
gleitenden Leiterbrücke beschränkt, also liegt eine "Queränderung" am
Rand der Leiterbrücke vor und damit Wirbel der eingeprägten Feldstärke E(e)
. E(e) ist der Grund für eine von 0 verschiedene
Ringspannung als Verschiebungsarbeit für einen vollen Umlauf pro
Ladungsmenge. Ein evtl. vorhandenes Potenzialfeld E kann zur
Ringspannung nichts beitragen, weil sich Anteile zur Verschiebungsarbeit
auf Teilstücken eines vollen Umlaufs gegenseitig aufheben. Die
Ringspannung ist es, die im geschlossenen Stromkreis wieder einen
Ringstrom hervorruft. Ist der Stromkreis nicht geschlossen, z.B. im
Falle einer isolierten Leiterbrücke, verschiebt E(e)
wieder Ladungen in der Leiterbrücke, die zur Ausbildung eines
elektrischen Feldes E führen. Nur der Anteil E ist ein
Quell- und ein Potenzialfeld. Der Vorgang ist beendet sobald sich
Kräftegleichgewicht gebildet hat, wenn also im Inneren der Leiterbrücke
gilt: E = - E(e).
Im (lokal) mit der Leiterbrücke mitbewegten BZS lässt sich für die
(dort) echte elektrische Feldstärke E' = v x B
der Wirbelcharakter mit Wirbeln (von E') ausschließlich am Rand
der Leiterbrücke nachweisen. Deswegen mag es erlaubt sein, E(e)
ein "elektrisches" Wirbelfeld zu nennen, obwohl es magnetischen
Ursprungs ist.
Im Falle des im "Magnetfeld bewegten Leiterbügels" (genauer: des in
einem BZS bewegten Leiterbügels, in dem ein Magnetfeld B
gemessen wird) gibt es also zwei korrekte
Beschreibungen der Entstehung einer Spannung.
(Ein solches Phänomen gibt es auch in anderen Situationen: Ein Elektron
bewege sich relativ zum Laborsystem. In ihm werden ein Magnetfeld und
ein elektrisches Feld gemessen. Dagegen gibt es im mit dem Elektron
mitbewegten Bezugssystem ausschließlich ein elektrisches Feld. Die
Aussagen in beiden BZS sind korrekt, nicht widersprüchlich. In der
Relativitätstheorie ist man es gewöhnt, das Bezugssystem zu wechseln und
dabei auch u.a. die Felder zu "transformieren".)
.
|
Was hat man von dieser Kenntnis über das
"eingeprägte" elektrische Wirbelfeld beim im Magnetfeld
bewegten Leiterstab?
|
- Das Grundsätzliche der Induktion wird herausgestellt: die
Entstehung einer Ringspannung bzw. eines "elektrischen"
Wirbelfelds bei jeder zeitlichen Änderung des
eingeschlossenen magnetischen Flusses. Es braucht
begrifflich nicht unterschieden werden zwischen
verschiedenen "Arten" der Induktion.
- Es wird erklärt, dass ein stationärer (oder
quasistationärer) Strom entstehen kann durch die
Energiezufuhr von außen, was für ein Potenzialfeld unmöglich
wäre.
- Entsprechend werden auch kompliziertere Situationen durch
das Wirbelfeld E(e) erklärt, wie etwa die
Induktion mit einer rotierenden Faraday-Scheibe im
Magnetfeld.
|
e) Induktion durch ein zeitabhängiges Magnetfeld bei
einem Kreisring mit eingebautem Widerstand (lehrreich, aber für
den Unterricht ungeeignet)
Der Kreisring außerhalb von R soll den Widerstand R' haben, der in
der Diskussion auch verschwinden könnte. Das Magnetfeld ändere sich so
langsam, dass stationäre Zustände der Ladungen und Felder jeweils
erreicht werden. Der Einfachheit halber soll der Kreisring aus einem
Leiter mit überall gleichem Querschnitt, aber Abschnitten
unterschiedlicher Leitfähigkeit σ bestehen. Die Leitfähigkeit σ des
"Widerstands" soll geringer sein als die des Rests.
|
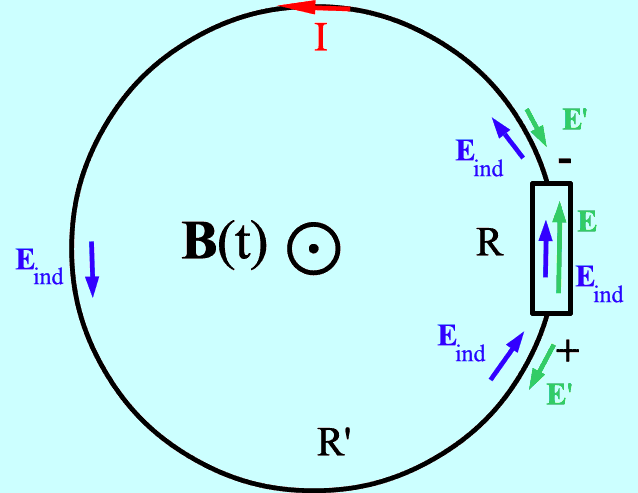
Abb. 8: Wenn sich der magnetische
Fluss Φ, der die Schleife senkrecht durchsetzt, in einer
bestimmten Weise verändert, entstehen ein Wirbelfeld Eind
(oder E(e)) und zum Beispiel eine
Ringspannung, die den eingezeichneten Ringstrom I hervorruft. Eind
ist - als Ursache von I - gleich orientiert wie I.
Die Induktionsspannung ist bei einer Flussänderungsrate
dΦ/dt: Uind = - dΦ/dt. Mit dem gesamten
Kreiswiderstand R + R' hat der Ringstrom in diesem Fall die
Stromstärke I = Uind / (R + R'). Am Widerstand liegt
die Spannung U = I·R. Sie ist im Fall R' = 0 gleich der
Ringspannung Uind $.
Nirgendwo können Ladungen verloren gehen oder hinzukommen: Das
drückt die Kontinuitätsgleichung aus. Die Stromdichte j
muss also überall längs des Kreisrings gleichen Betrag haben.
Erfahrungsgemäß gilt das Ohm'sche Gesetz. Es legt dann eine
Bedingung fest: Wegen j = Ex/σx
mit Größen im jeweiligen Leiterabschnitt muss im Bereich
geringerer Leitfähigkeit σx eine größere elektrische
Feldstärke Ex herrschen. Wie kann das
erreicht werden?
Bei Stromfluss entstehen an den Enden des Widerstands R Oberflächenladungen
(Raumladungen in der Grenzschicht), die im Widerstand R ein
zusätzliches elektrisches Feld E hervorrufen
(gleichgerichtet zu Eind im Widerstand),
ebenfalls ein elektrisches Feld E' außerhalb des
Widerstands, dessen Stärke und Verlauf hier nicht untersucht
wird. Dabei würden komplizierte Oberflächenladungen
eine Rolle spielen, die dafür sorgen, dass beide Felder, E
und E', irgendwie dem Leiterverlauf folgen. Die
Orientierungen der Felder sind in der Zeichnung angedeutet. E
verstärkt im Inneren des Widerstands das induzierte Feld
Eind, wenn die Leitfähigkeit im
Widerstand geringer als im Kreisring ist; außerhalb heben sich
Eind und E' ganz oder
teilweise auf, je nach den Leitfähigkeiten.
Die Felder E bzw. E' sind - da von Ladungen
erzeugt - Potenzialfelder. Ihnen ist das durch die Induktion
entstandene Wirbelfeld Eind überlagert. Das
gesamte Feld ist weder ein reines Wirbelfeld noch ein reines
Potenzialfeld. Induktion manifestiert sich primär im
Wirbelfeld-Anteil. Ein Potenzialfeld-Anteil könnte zum Nachweis
genutzt werden.
Ein elektrisches Wirbelfeld gleicher Größe entsteht
übrigens auch, wenn der Kreisring nichtleitend oder nur
gedacht ist. Es kann dann keinen Ringstrom erzeugen. |
Kann ein (reines) Potenzialfeld
einen dauernden stationären Strom hervorrufen?
Aus energetischen Gründen nicht. Ein Potenzialfeld ist
energieerhaltend. Wenn Mechanismen wirksam sind, die Wärme
produzieren, wird Energie entzogen, aber nicht ersetzt. Zum Ersatz
solcher Energieverluste muss von außen Energie zugeführt werden
mittels eines Nicht-Potenzialfelds, also eines Wirbelfelds.
Auf Schulniveau wird das mit einem Analogieversuch gezeigt:
 |
Abb. 8: Ein Wasserstromkreis wird durch eine
Pumpe angetrieben. Der Stromkreis kann durch ein
Potenzialfeld (Gravitationsfeld) beliebig geführt werden.
Selbst, wenn die Leitungen bis zum Mond geführt würden
(und wieder zurück), hätte das - wenn er einmal zustande
gekommen ist - keinen Einfluss auf den Stromfluss, der
allein von der Pumpe angetrieben wird. Die Pumpe bezieht
Energie von außen. Bei steigenden Stücken der Leitung
würde für ein Wasserteilchen die potenzielle Energie
zunehmen, beim gleichzeitigen Herabströmen anderer
Wasserteilchen aber in gleichem Maße wieder abgegeben
werden. Insgesamt spielen die Änderungen der potenziellen
Energie dabei keinerlei Rolle. Das ist ein Effekt, der
sich durch ein Teilchenmodell für die mit dem Strom
angeblich unabhängig voneinander transportierten
"Ladungen" allein nicht erklären lässt. Hier spielen auch
Kontinuitätsgleichung und Strömungslehre herein:
Energieänderungen müssen für die ganze bewegte Wassermenge
betrachtet werden.
|
 |
Abb. 9: Eine Scheibenwischerpumpe als
Energielieferant zum Wasserstromkreis für Energie von außen. |
Daraus entwickelt sich das "Pumpenmodell
des elektrischen Stromkreises": In
einem elektrischen Stromkreis finden zwei Transportvorgänge
zugleich statt: 1. der Transport von elektrischen Ladungen, und 2.
der Transport von Energie. Die elektrischen Ladungen sind wie das
Wasser im Wasserstromkreis schon immer im elektrischen Stromkreis
vorhanden. Durch die Strom-/Spannungsquelle als Pumpe werden sie
in Bewegung gesetzt. Das Fließen dieser Ladungen heißt
elektrischer Strom. Die Ladungen fließen immer im Kreis herum.
Zugleich wird mit der Pumpe Energie zugeführt, die mit
Hilfe des Stroms zu einem
"Verbraucher" transportiert oder dort abgegeben wird. Die Bewegung
der Ladungen dient als Vehikel für den Energietransport; auf
welchem Weg letzterer geschieht, wird in der Schule
nicht angesprochen. Je größer die Spannung U ist, desto
größer ist die "Pumpenstärke". Je größer die "Pumpenstärke" ist,
desto mehr Ladungen pro Zeiteinheit können bei unverändertem
Stromkreis durch einen Leiterquerschnitt transportiert werden,
desto größer ist die Stromstärke I (Maß für die Anzahl der pro
Zeiteinheit durch einen Leiterquerschnitt transportierten
Ladungen). Je größer die "Pumpenstärke" U und die Stromstärke I
sind, desto größer ist die pro Zeiteinheit transportierte Energie.
Ihr entspricht die Leistung P = U·I. Die Pumpenstärke/Spannung ist
charakteristisch für die Pumpe/Strom-/Spannungsquelle, die
Stromstärke für den ganzen Stromkreis inkl. Leitungen und "Pumpe".
Das "Pumpenmodell" umgeht die Problematik "Potenzialfeld oder
Wirbelfeld".
Das "Pumpenmodell" ist äquivalent zum "Modell des
geschlossenen Heizungsstromkreises", bei dem ebenfalls zwei
Transportvorgänge gleichzeitig stattfinden, der Transport von Wasser
und der Transport von innerer Energie des Wassers, diesmal beides
zugleich durch die Leitungsrohre.
Die Notwendigkeit eines Wirbelfelds für einen
stationären Strom lässt sich auch theoretisch nachweisen:
Vgl. Der
stationäre Strom im geschlossenen Stromkreis
.
|
Was hat man von dieser Kenntnis?
|
- Mit dem "Pumpenmodell" (zu unterschieden vom
ebenfalls problematischen Druckmodell) steht ein
einfacheres Modell als das "Höhenmodell" für die
Spannung in einem Stromkreis zur Verfügung. Beim
Höhenmodell besteht die Gefahr, dass Ladungs-Anhäufungen
übersehen oder wenigstens nicht beachtet werden. Es
neigt dazu zu suggerieren, dass die transportierte
Energie in den Ladungen konzentriert sei (wie etwa auch
das so genannte "Nektar-Bienen-Modell").
|
.
Didaktische Folgerungen
- Ich meine, dass an der Schule die Problematik "Potenzialfeld
oder nicht" nicht diskutiert werden sollte. Es sollten m.E. jedoch
falsche Aussagen vermieden werden. M.E. sollte deshalb in diesem
Zuammenhang überhaupt nicht von einem Potenzial gesprochen werden.
- Als einfachstes korrektes Modell des elektrischen Stromkreises,
das nicht in Gefahr steht, gegen die Problematik "Potenzialfeld
oder Wirbelfeld" zu verstoßen, erscheint mir das Pumpenmodell bzw.
das Modell des geschlossenen Heizungsstromkreises.
- Dass bei moderneren Modellen des Stromkreises die potenzielle
Energie so in den Vordergrund gestellt wird, hat wohl damit zu
tun, dass man den Arbeitsbegriff in den Hintergrund schieben
möchte. Wie man unschwer an diesem Text erkennen kann, hat der
Arbeitsbegriff m.E. auch für die Schule einen hohen Erklärungswert
und vermeidet Falschaussagen.
- Bei der Induktion entsteht immer ein elektrisches Wirbelfeld
(im Sinne von E + E(e)). Es ist
mit einer nicht verschwindenden Ringspannung (Umlaufsspannung)
verbunden.
- Spannung sollte nicht definiert werden als Potenzialdifferenz
(gilt nur bei Vorliegen eines Potenzialfelds), sondern als
spezifische Verschiebungsarbeit (Verschiebungsarbeit
pro Ladung; gilt allgemein). So kann man auch eine
Ringspannung (Umlaufsspannung) für einen geschlossenen Weg
definieren, die charakteristisch ist für die Induktion.
- Weil das Feld im Außenraum einer Monozelle dem Potenzialfeld
eines geladenen Kondensators entspricht, kann das "Höhenmodell"
(Höhenunterschied entspricht Potenzialdifferenz) für die Spannung
einige Fakten des Stromkreises plausibel machen. Es verschleiert,
dass die Energie von außen geliefert werden muss und auch als
nichtelektrische Energie geliefert werden kann. Es verschleiert,
dass zusätzliche Potenzialfelder im Stromkreis für den "Antrieb"
keine Rolle spielen, sondern nur die Ringspannung. Wenn schon
Höhenmodell, dann sollte nicht die Höhe eingehen, aus der der
"freie" Stromfluss startet, sondern die Höhe, auf die die Pumpe
die Ladungen pumpen kann (obwohl beide zahlenmäßig, aber nicht
begrifflich, identisch sind). Was legt die erreichbare Höhe fest?
Nur die Pumpe!
- Strenggenommen muss man sich bei Verwendung von
Potenzialdifferenzen im Rahmen der Induktion auf Fälle mit
unterbrochenem Leiterkreis beschränken, wo aus der Ringspannung
zusätzlich eine gewöhnliche (Klemmen-)Spannung entstanden ist. Das
Wesentliche der Induktion - das Entstehen eines Wirbelfelds - wird
verschleiert, Lernhindernisse werden aufgebaut.
Vieles, was hier erläutert wurde, darf im Schulunterricht nicht
gebracht werden. Den Versuch einer Darstellung der
elektromagnetischen Induktion für den Unterricht finden Sie
hier.
.
Vgl. auch Fragen und
Antworten
Vgl. auch Hat Spannung bei einem
stationären Strom etwas mit "gestauten Elektronen" zu tun?
und auch Spannungsdefinition "über
potenzielle Energie der frei beweglichen Elektronen"?
Hinweise zur Präzisierung:
1. Eine Umlaufs- oder Ringspannung U kann definiert
werden als Verschiebungsarbeit für einen geschlossen Weg pro
verschobener Ladungsmenge q: U = WAA/q . Im Prinzip wäre
das auch im Gravitationsfeld möglich, wobei q durch die Masse zu
ersetzen ist, doch ist dort eine Umlaufsspannung belanglos, da sie
(im Potenzialfeld) immer 0 ist. W enthält meistens elektrische
Anteile; wie wir gesehen haben, kann sie aber auch nichtelektrische
Anteile (z.B. von chemischen Kräften oder von der Lorentz-Kraft)
enthalten. Bei einer rein elektrischen Arbeit - wie bei der
Induktion durch ein zeitlich veränderliches Magnetfeld - gilt: U =
∫o E·dr (Umlaufsintegral für einen geschlossenen Weg
von einem Punkt A zu ihm zurück).
2. Wenn ein Potenzialfeld vorliegt mit einem Potenzial Φ, erhält
man die Feldstärke E durch Gradientenbildung: E = -
grad φ. E ist dann ein wirbelfreies Feld, wie auch die
Vektoranalysis lehrt: rot E = rot grad φ = 0. E
besitzt dann Quellen und Senken: div E = ρ/ε0 mit
der elektrischen Feldkonstanten ε0.
3. Wenn ein reines Wirbelfeld (also ohne Quellen und
Senken) vorliegt, gelten die Beziehungen: rot E =/= 0 und
div E = 0, im allgemeinen Wirbelfeld zumindest rot E
=/= 0.
4. Was bedeutet "negative
Verschiebungsarbeit"? Bei positiver Verschiebungsarbeit wird
durch eine äußere Kraft Energie aufgewendet, bei negativer
Verschiebungsarbeit wird dementsprechend Energie nach außen
abgegeben. Wie kann das geschehen?
Nehmen wir an, wir führen eine positive Probeladung nahe an die
positive Kondensatorplatte heran. Dazu müssen wir positive
Verschiebungsarbeit aufwenden. Allgemein: Hat man im Potenzialfeld
einem Probekörper Energie zugeführt, die als potenzielle Energie
gespeichert ist, dann wird diese potenzielle Energie frei, indem der
Probekörper anschließend beschleunigt wird (die positive Probeladung
in Richtung negativer Kondensatorplatte). Das wäre zunächst ein
energieerhaltender Vorgang: potenzielle Energie wird in kinetische
Energie umgewandelt und bleibt so zunächst dem System erhalten. Um
das zu verhindern müssen wir eine (äußere) Bremskraft auf den
Probekörper ausüben, die eine Beschleunigung verhindert. Durch diese
Bremskraft wird Energie nach außen abgeführt.
6. Ein stationärer Strom ist ein Strom,
durch den nicht im Laufe der Zeit irgendwo im Stromkreis Ladungen
angehäuft oder entfernt werden. Gemäß der Kontinuitätsgleichung
bedeutet das: div j = - ∂ρ/∂t = 0.
7. Nach Aussage des Poynting-Vektors (Energiestrom-Vektors)
S = E x B fließt die Energie nicht durch den
Leiter, sondern durch den von E und B erfüllten Raum
zwischen den Leitern zum "Verbraucher". Der Strom ist lediglich ein
Vehikel für den Energietransport. Vgl. Becker
8. Umlaufsintegral
Für ein Feld V ist das Umlaufsintegral folgendermaßen
definiert: U =∫o V·dr . Dabei bedeutet das Symbol ∫o
.... ·dr das Linien-Integral über einen geschlossenen
Weg.
9. "Lorentz-Induktion" in der Schule
In der Schule wird die Induktion in der Regel mit der Lorentz-Kraft
in einem "bewegten Leiter" erklärt. (Gemeint ist: in einem Leiter,
der sich in einem Bezugssystem bewegt, in dem eine magnetische
Flussdichte B gemessen wird: Jeder Leiter ist schließlich
bewegt und zugleich in Ruhe - je nach Bezugssystem.)
Da in dieser Erklärung die Ringspannung stillschweigend durch eine
gewöhnliche Spannung gemessen wird, die aus einem sekundären
elektrischen Feld entsteht, ist die Herleitung korrekt in einem
nicht zu einem Leiterkreis geschlossenen Stab.
Es gibt schließlich zwei Möglichkeiten, die bei der Induktion
entstehende Ringspannung U zu messen:
1. Durch einen Ringstrom I = U/R in einem geschlossenen Leiterkreis
mit dem Widerstand R.
2. Durch die Umwandlung in eine gewöhnliche Spannung
(Potenzialdifferenz) in einem nicht geschlossenen Kreis, z.B. in
einem Leiterstab.
$ Daraus ergibt sich eine weitere
Messmöglichkeit für die Ringspannung.
*) "Verschiebungsarbeit" steht in
allgemeineren Fällen für ein Linienintegral (Wegintegral) über die
Feldstärke.
.
.
( zuletzt aktualisiert: 2013 ; Zeichensatz korrigiert: 2019
; einige Präzisierungen zur Vermeidung von Missverständnissen:
2022)









