Biphotonen (Photonenzwillinge) sind Quantenobjekte aus zwei verschränkten Photonen, die selbst aber ohne eine Messung keine individuellen Eigenschaften haben. Sie sind charakterisiert durch die Eigenschaften des Gesamtzustands, z.B. seinen Impuls, Drehimpuls bzw. seine Polarisation. Wäre der Gesamtimpuls eines Biphotons z.B. 0, wäre nach Messung des Impulses p von einem Einzelphoton, wenn also der Zweiteilchen-Zustand aufgebrochen ist in Einteilchen-Zustände, unmittelbar klar, dass dann der Impuls des so entstandenen zweiten Einzelphotons -p sein muss. Das regelt der Impuls-Erhaltungssatz. Mit Biphotonen können Experimente im Sinne des Einstein-Podolsky-Rosen-Paradoxons (EPR) gemacht werden. Solche Biphotonen-Zustände gibt es in der klassischen Physik überhaupt nicht. Sie lassen sich weder durch ein Teilchenmodell noch durch ein Wellenmodell mit Wellen im uns umgebenden Anschauungsraum korrekt beschreiben.

Biphotonen können z.B. mit einer Zweiphotonen-Quelle mittels parametrischer Fluoreszenz (parametric down conversion) erzeugt werden. Solche Biphotonen sind verschränkt bzgl. der Polarisation und des Impulses. Misst man aber - nach Aufbrechen des Zweiteilchen-Zustands - einzelne Photonen, so können diese i.A. zeitlich und räumlich unkorreliert nachgewiesen werden. Mit einem nachgeschalteten Mach-Zehnder-Interferometer können die Photonen eines Biphotons zeitlich und räumlich korreliert werden. Das wurde von Hong, Ou und Mandel realisiert. Diese Lichtquelle soll hier nach ihren Erfindern HOM genannt werden.

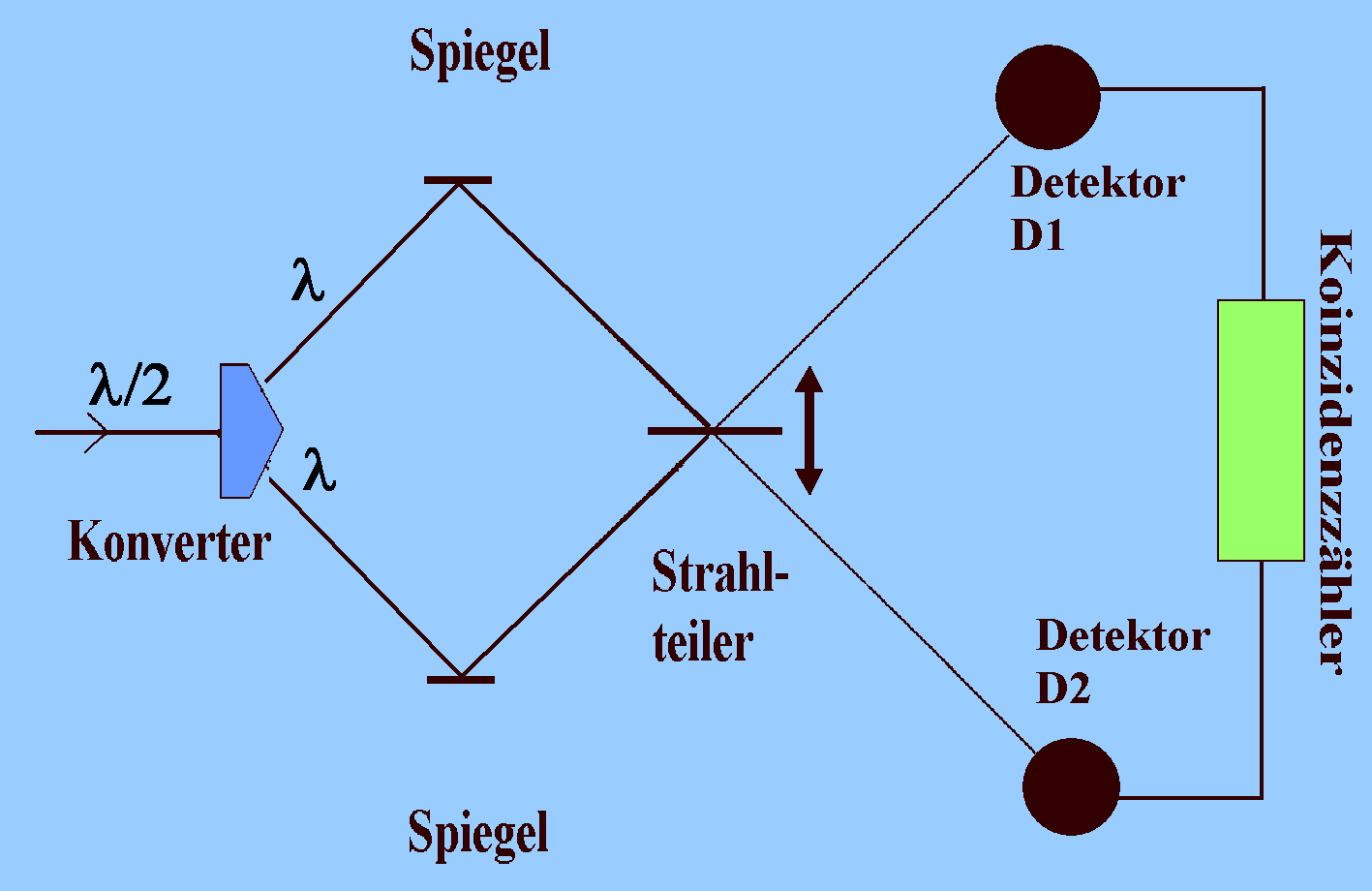	Am Ausgang von HOM befindet sich ein halbdurchlässiger Spiegel (Strahlteiler). Den Konverter verlässt ein Photonenzwilling oder Biphoton aus zwei bzgl. Polarisation und Impuls verschränkten Photonen, die ohne eine Messung keine individuellen Eigenschaften haben. Es wird dafür gesorgt, dass sie bei Messungen ununterscheidbar sind. Sie stimmen dann überein in Polarisation, Entstehungszeit und Energie (Wellenlänge). Ein Koinzidenzzähler registriert, wenn beide Detektoren D1 und D2 an den Ausgängen des Strahlteilers gleichzeitig ansprechen.
Ist der Strahlteiler symmetrisch angeordnet, so dass beide Zweige des Interferometers gleich lang sind, kommt es fast nie zur Koinzidenz: Dann erscheinen beide Photonen quasi immer am gleichen Ausgang. Das kann aber einmal der eine, dann wieder der andere sein, gemäß dem "objektiven Zufall". Immer registriert jeder Detektor für sich eine unregelmäßige Folge von Photonen. Nur in der Koinzidenz wird erkennbar, dass beide Photonen verschränkt waren, einem Biphoton angehörten. Für die weitere Überlegung ist es wichtig, die Phasenverschiebungen bei den Reflexionen zu beachten. Nach der Literatur gibt es unterschiedliche Typen von Strahlteilern: Bei der Reflexion an Strahlteilerspiegeln, entsteht, wenn der Strahl aus der Luft (Reflexion vom Typ L) kommt, ein Phasensprung von π, nicht aber, wenn der Strahl aus dem Glaskörper des Spiegels kommt (Reflexion vom Typ G). *) Die tatsächlichen Phasenverschiebungen sind belanglos. Wichtig ist nur, dass zwischen Situation (1) und Situation (2), und später zwischen (4) und (3) ein Phasenunterschied von π besteht. Das ist auch der Fall bei Strahlteilerwürfeln, bei denen der Phasenunterschied zwischen reflektiertem und durchgelassenen Strahl gerade π/2   ist.
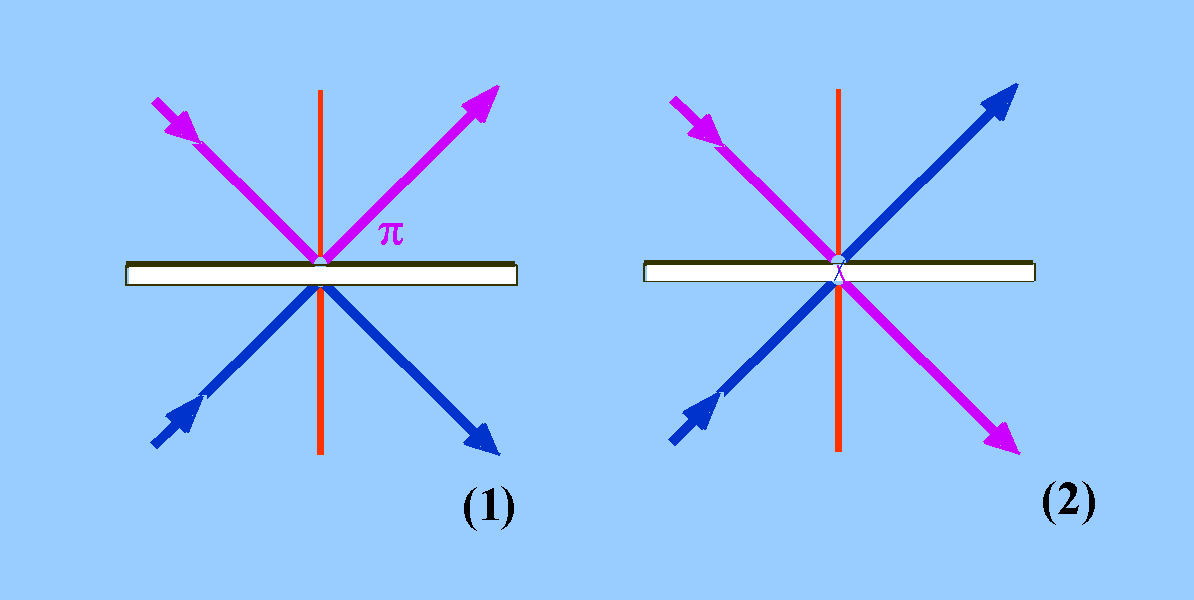	Dass dann beide Photonen am gleichen Ausgang erscheinen müssen, kann man relativ leicht verstehen. Denn dann kann zwischen zwei "klassisch" denkbaren Situationen nicht unterschieden werden: nämlich dass a) die beiden nicht unterscheidbaren Photonen reflektiert werden (1) oder dass b) beide hindurchgehen (2). U.a. kommt es zur destruktiven Interferenz (Zweiteilchen-Interferenz):
Hier wird zunächst das Verhalten von zwei Einzelphotonen (magenta und blau) am Strahlteiler untersucht. Sie treten von unterschiedlichen Seiten her in den Strahlteiler ein. Zwischen den beiden klassisch denkbaren Möglichkeiten für den Austritt der Photonen kann nicht unterschieden werden, also kommt es zur Interferenz. Im Minimum verschwindet die Wahrscheinlichkeit für eine Koinzidenz für den gleichzeitigen Nachweis von zwei Photonen. Das Biphoton (das Photonenpaar) wird einen der beiden Ausgänge wählen.
In diesem Fall verschwindet die Wahrscheinlichkeit für eine Koinzidenz zwischen beiden Ausgängen. An welchem Ausgang beide Photonen des Biphotons erscheinen; ist zufällig. Justiert man also die Abstände durch Bewegung des Strahlteilers in Pfeilrichtung so ein, dass beide Photonen jeweils nur einen Ausgang nehmen, erkennbar an fehlenden Koinzidenzen, kann man sicher sein, ein verschränktes und "räumlich stark korreliertes" Photonenpaar (ein solches Biphoton) erzeugt zu haben. Für diese beiden Fälle zeigt auch eine vereinfachte theoretische Überlegung (siehe unten) eine verschwindende Koinzidenzwahrscheinlichkeit an. Bemerkenswert ist, dass sich beide Photonen in diesem Fall völlig gleich verhalten: Entweder werden sie beide reflektiert oder sie gehen beide durch den Strahlteiler.	Aus Beobachtungen an einem der Einzelphotonen kann man dann zurückschließen auf das Verhalten des anderen. Das ist typisch für ein Biphoton (Photonenzwilling bzw. verschränkte Photonen).
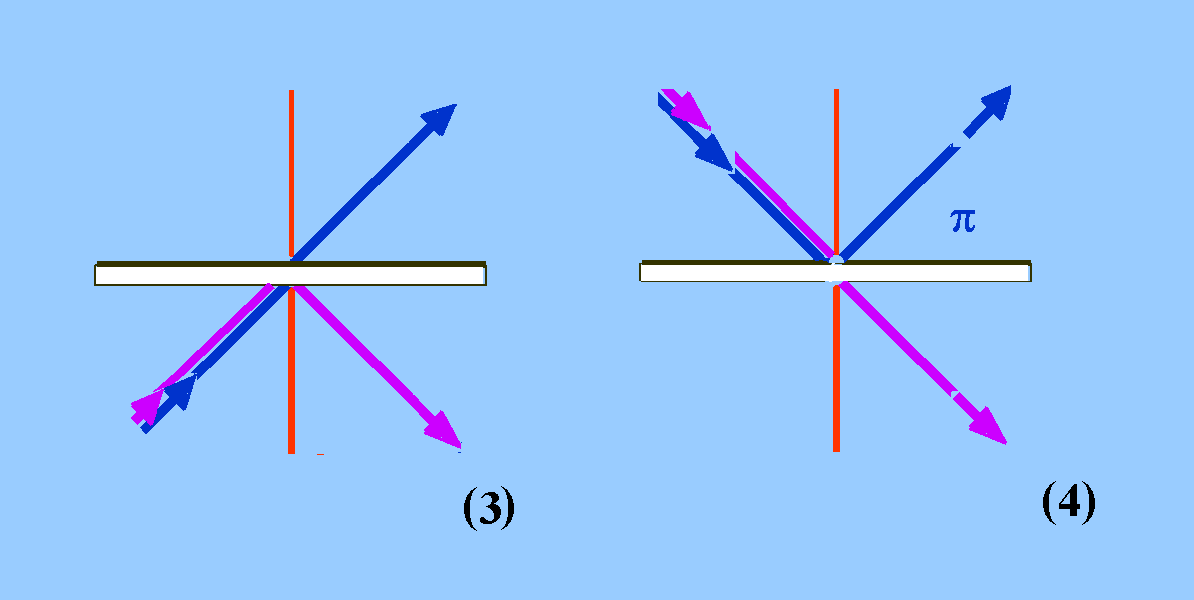
Weitere Beiträge mit Austrittsmöglichkei­ten, zwischen denen nicht unterschieden wird. Hier treten beide Photonen von der gleichen Seite her in den Strahlteiler ein.	(3) und (4) stellen aber noch zwei andere Möglichkeiten dar, wenn  die Wahrscheinlichkeit untersucht werden soll, dass es zur Koinzidenz zwischen beiden Ausgängen des Strahlteilers kommt. Nur bei der Möglichkeit (4) entsteht  - bei einer bestimmten Orientierung des Strahlteilers - ein Phasensprung von π. Auch hier wird nicht zwischen den beiden Austrittsmöglichkeiten entschieden: Es kommt auch hier zur Interferenz der Biphotonen. Die beiden Anteile heben sich weitgehend gegeneinander weg. Ein Problem entsteht nur, wenn die beiden Photonen nicht phasengleich aus der Quelle austreten. Wir werden dies im Anhang mit einer Phasenverschiebung ß berücksichtigen, die tatsächlich nach Rode bzw. Gosh und Mandel nicht zeitlich konstant ist.
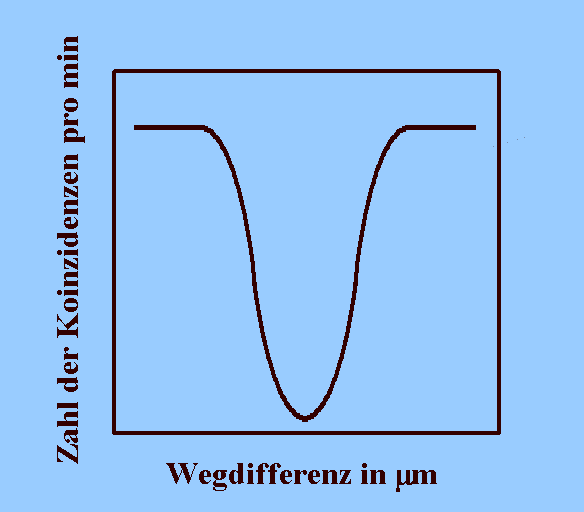
Nach Hong, Ou und Mandel, schematisch	Messergebnis: Wenn die Wegdifferenz zwischen beiden Interferometer-Armen 0 ist, ist die Koinzidenzrate (fast) 0. Es kommt dann (fast) nie vor, dass beide Detektoren ansprechen. Die beiden Photonen treten dann gemeinsam bei einem bestimmten Ausgang aus und sind dann stark "räumlich korreliert". Bei größeren und kleineren Wegdifferenzen zwischen beiden Armen des Interferometers werden Koinzidenzen registriert: Ein Teil der Photonen eines Paars erreichen beide Detektoren gleichzeitig. Sie sind dann schwach oder gar nicht räumlich korreliert. Grund für Breite und Form des Grabens seien Eigenschaften des Biphotons von der Erzeugung her. Vage wird gesagt, das habe etwas damit zu tun, wie "die Wellenpakete beider Einzelphotonen zusammenpassen". Bei perfekter Übereinstimmung falle die Koninzidenzrate auf 0 ab. Bei unterscheidbaren Photonen entstehe dagegen kein Minimum.

Die HOM-Anordnung (ohne Detektoren und Koinzidenzschaltung) dient für andere Versuche als Quelle von räumlich korrelierten Biphotonen, wie z.B. beim Ostermeyer-Versuch. Solche Biphotonen verlassen dann - klassisch gesprochen - gleichzeitig am gleichen Ort den Strahlteiler und sind ununterscheidbar. Die HOM-Anordnung ist auch eine Grundlage für die Quantenkryptographie.

Der Versuch kann mit Geräten der Universität Erlangen (Prof. Dr. Meyn) auch auf dem Bildschirm durchgeführt werden: http://www.didaktik.physik.uni-erlangen.de/quantumlab/

Es gibt erweiterte Anordnungen des HOM-Versuchs (z.B. S. Zotter 2009), die auch für diese Zweiteilchen-Interferenz nachweisen:

Der Nachweis der destruktiven  Zweiteilchen-Interferenz beim HOM-Versuch durch die Quantentheorie erfolgt (vereinfacht) folgendermaßen: Die Verbindungsstrecken zwischen Quelle und Detektoren seien gleich lang mit der Länge s.

Die Ausbreitung von Wellen kann durch Wellenzahlvektoren k beschrieben werden, wobei k =  /k/ = 2·π/λ.

Beim Austritt aus der Quelle seien die "Wellenfunktionen" der beiden Einzelphotonen Ψ1 · eiß und Ψ2 (Ψ1 = Ψ2). Das Photon 1 (nach oben) soll gegenüber Photon 2 (nach rechts) eine Phasenverschiebung ß haben. Deswegen enthält die Wellenfunktion von Photon 1 immer noch einen Faktor eiß . Bei der Ausbreitung ebener Wellen (für die "Wellenfunktion der Photonen") kommt  bei einer Laufstrecke s jeweils ein Faktor ei·k·s hinzu, der aber  bei symmetrischer Anordnung für jedes Photon derselbe ist, und nicht explizit angeschrieben wird. Weiter sind Faktoren eiπ = -1 hinzufügen, wenn eine Reflexion vom Typ L erfolgt (grün). 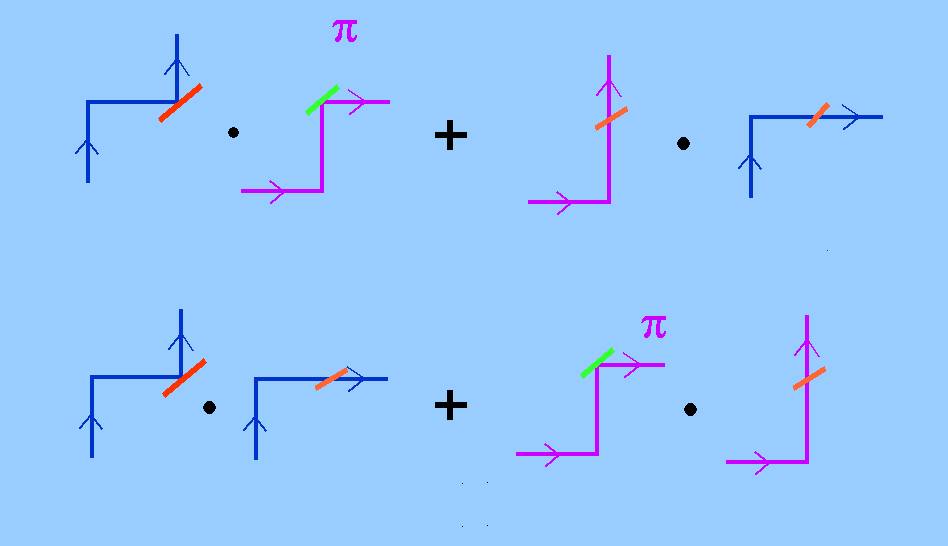Die nebenstehende Graphik kennzeichnet symbolisch alle Möglichkeiten für den Eintritt je eines Photons in Detektor 1 und Detektor 2. Bei jedem Photon erfolgt genaue eine Reflexion am Umlenkspiegel, die auch einen Faktor eiπ = -1 hinzufügt, der aber weggelassen wird, weil er für alle Photonen der gleiche ist. Der Strahlteiler ist jeweils symbolisiert. In der ersten Zeile stehen die zwei Möglichkeiten für nach klassischer Vorstellung getrennt laufende Photonen, in der zweiten Zeile zwei Möglichkeiten für nach klassischer Vorstellung jeweils gleich laufende Photonen des Photonenzwillings.

Es soll jetzt die Wahrscheinlichkeit berechnet werden, dass beide Detektoren in Koinzidenz ansprechen. Dazu versuchen wir ohne Beachtung der Polarisation das Betragsquadrat einer Zweiphotonen-Wellenfunktion Ψ(x,x,t) zu berechnen. Die Wellenfunktionen der Einzelphotonen seien bei der Quelle Ψ₁ · e^iß  und Ψ₂ (beides komplexwertige Zahlen, die auch einen zeitabhängigen Exponentialfaktor vom Betrag 1 enthalten),  bei den Detektoren schließlich

Ψ₁ · e^iß·Ψ₂ · e^iπ  +   Ψ₁ · e^iß ·Ψ₂ =  Ψ₁ ·Ψ₂ · e^iß (-1 + 1) = 0               für die ersten zwei Möglichkeiten und

Ψ₁ · e^iß·Ψ₁· e^iß  +   Ψ₂ ·Ψ₂  · e^iπ   =  Ψ₁·Ψ₁ · ( e^i2ß  - 1)                        für die letzten zwei Möglichkeiten ^*)

da  Ψ₁ = Ψ₂.

Wenn keine Phasenverschiebung zwischen beiden in der Quelle erzeugten Photonen besteht (ß = 0), verschwinden beide Terme. Dann ist also die Koinzidenz-Wahrscheinlichkeit (Betragsquadrat!) 0. Beide Photonen (das Biphoton) treten dann aus demselben Ausgang des Strahlteilers aus. Man kann auch nachweisen, dass das mit 50%iger Wahrscheinlichkeit bei dem einen oder dem anderen geschieht. Das kommt dem Versuchsergebnis schon sehr nahe.

Wenn im zweiten Fall ß =/= 0,  klammern wir e^iß aus und erhalten  Ψ₁· Ψ₁ · e^iß · ( e^iß  - e-^iß ) =  2·i · Ψ₁·Ψ₁ · e^iß · sin(ß). In diesem Fall ist das Betragsquadrat proportional zu sin²(ß). Wenn /ß/ klein, ist die Koinzidenzrate nahe 0, proportional zu ß². 

Bei der Emission könnte aber auch das 2. Photon einen Phasenvorsprung erhalten. Dann wäre das Photon 2 mit dem Faktor e^iß zu versehen und es würde sich ergeben:   Ψ₁· Ψ₁ · ( 1 - e^i2ß ) = -  2·i·Ψ₁·Ψ₁ · e^iß · sin(ß). Beide Sinus-Anteile sind - da es sich bei Photonen um Bosonen handelt - zu addieren und die Summe zu halbieren. Auch diese Anteile heben sich vollständig weg, und es sollte sich eine exakte Nullstelle für die Koinzidenzwahrscheinlichkeit ergeben. Auf eine Phasenverschiebung zwischen den Einzelphotonen bei der Erzeugung der Biphotonen kommt es bzgl. der Nullstelle der Koinzidenzrate offenbar nicht an.

Der Versuch gelingt nicht mit zwei Einzelphotonen, zu deren Nachweis man auch zwei nicht in Koinzidenz geschaltete Detektoren braucht.

Wie man diesem Text hier unschwer entnehmen kann, bin ich allerdings nicht mit allen Aussagen von Herrn Rode einverstanden.

Vgl. auch ein Erratum: MNU 64/8, S. 504 (2011) und      http://www.mnu.de/attachments/466_MNU_Heft_2011_8_Rode_Photonen.pdf

C. K. Hong, Z. Y. Ou, and L. Mandel, "Measurement of subpicosecond time intervals between two photons by interference", Phys. Rev. Lett. 59, 2044 (1987)

R. Gosh and L.Mandel, "Observation of Nonclassical Effects in the Interference of  Two Photons", Phys. Rev. Lett. 59, 1903-1905 (1987)

S. Zotter, "Entangled Photon Experiments with a Fast Interferometric Switchable Beam Splitter",. Diplomarbeit Uni Wien, 2009

Vgl. auch V34 Hanbury-Brown/Twiss-Experiment: (1) räumliche (transversale) Kohärenz

^*) Wenn bei jeder Reflexion ein Phasensprung von π/2 gegenüber dem durchgehenden Strahl auftritt (also - π/2 vom durchgegehenden gegenüber dem reflektierten), würde das gleiche Ergebnis herauskommen. Es würde sich z.B. für die Anteile (3) und (4) ergeben:  Ψ₁ · e^iß · e^iπ/2 · Ψ₁ · e^iß  +   Ψ₂ · Ψ₂  · e^-iπ/2   =  Ψ₁ · Ψ₁ · e^{iπ /2} ( e^i2ß  - 1) , da auch e^-iπ   = -1 . Beim Betragsquadrat würde der Exponentialfaktor e^{iπ /2} wegfallen: Gleiches Ergebnis wie oben!